Морозов Введение в теорию горячей плазмы Част2 2013

θ′−θ ≈ vRq||t′ ; ζ′−ζ ≈ q(θ′−θ);

k(θ′−θ)−l(ζ′−ζ)≈ (k −lq)(θ′−θ)= v||t′(k −lq).

Rq

Отклонением пролётных частиц от магнитной поверхности можно пренебречь. Интегрирование по времени дает множитель

ления. Эта частота существенно меньше обратного времени пролёта электрона вдоль одного оборота силовой линии по тороидаль-

мода не слишком близка к резонансу, k ≠ lq. В этом случае множи-

тель (3.7.13) мал и вкладом от пролётных частиц можно пренебречь.

Для запертых частиц можно написать ([8])

Характер траектории можно хорошо видеть на примере глубоко запертых частиц:

61

Частицы совершают периодические колебания по углу θ. По углу ζ наряду с колебаниями они совершают также поступатель-

ное движение со скоростью Vζ , < ξ′ >=Vζt . Таким образом, инте-

грирование по t′ можно свести к интегрированию по периоду колебаний, соответствующему колебаниям между точками отражения и суммированию по этим отрезкам времени. Тогда мы получим интегральное уравнение

переходя к интегрированию по θ′ от интегрирования по t′. В результате находим интегральное уравнение для ϕ(θ). Решая его,

получаем собственные функции и собственные значения для частоты. Условие устойчивости, при котором Imω = 0, имеет вид

личина q растёт с радиусом. Таким образом, неустойчивость на

запертых частицах должна развиваться и приводить к аномальным переносам практически при любом профиле тока. Более подробно эта неустойчивость описана в работе [5].

ГЛАВА 4. РЕЗИСТИВНЫЕ НЕУСТОЙЧИВОСТИ

4.1. Тиринг-мода

Рассмотренные в предыдущей главе неустойчивости идеальной плазмы развиваются, как правило, за очень малые времена порядка отношения размера плазмы к альфвеновской скорости. В плазме могут развиваться и другие неустойчивости, связанные с конечной её проводимостью. Характерные времена их развития существенно больше, однако и они играют важную роль. За такие времена нарушается вмороженность силовых линий в плазму. В частности,

62

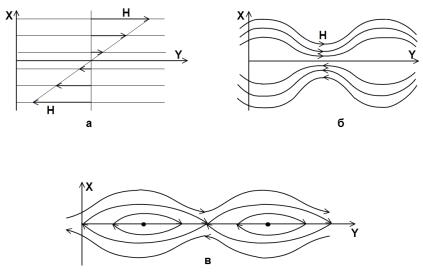
может происходить перезамыкание силовых линий и меняться топология магнитного поля. Пример такого перезамыкания приведён на рис. 11.

Рис. 11. Перезамыкание силовых линий

Пусть в плоском слое плазмы течёт ток в направлении оси z. Силовые линии в начальный момент времени параллельны оси y

(рис. 11, а). Такая конфигурация может быть неустойчивой. Как известно, параллельные токи притягиваются, поэтому однородный вначале ток начинает расслаиваться на отдельные волокна. Силовые линии начинают изгибаться (рис. 11, б). Токи, текущие вблизи поверхности x = 0 , при конечной проводимости гасят друг друга (в случае бесконечной проводимости они лишь сгущались бы вблизи этой поверхности), и магнитные поверхности меняют топологию, образуя «островную» структуру (рис. 11, в).

Опишем эту картину математически. Пусть H0 = H0y (x)ey + H0zez . Закон Ома в простейшей форме имеет вид

63

Для простоты будем считать, что удельное сопротивление по-

Преобразуем первый член в правой части уравнения с учётом

Тогда уравнение (4.1.2) можно переписать в виде уравнения

Здесь мы учли, что rot rot H = −∆H .

К этому уравнению необходимо добавить уравнение, описывающее движение плазмы. В одножидкостном приближении, прене-

Членом (V, )V мы пренебрегли, так как он квадратичен по V и в линейное приближение вклада не даст. Последний член в пра-

Множитель ½ перед последним членом в правой части связан с тем, что оператор «набла» действует лишь на одно Н в левой. Представим Н как сумму невозмущённого поля и малого возмущения, подставим (4.1.6) в (4.1.5). В нулевом приближении получим

64

Правую часть и левую части этого уравнения с точностью до постоянного множителя можно представить в виде

Здесь мы предположили, что плазма несжимаема, ( ,V)= 0.

Все коэффициенты перед H и v в уравнении (4.1.11) только от х, и уравнение можно разложить в интеграл Фурье по у, z и t,

V = Vω,ky ,kz exp(γt + ky y + kz z). В дальнейшем индексы у фурье-

компонент будем опускать. Итак, в фурье-представлении уравнение (4.1.9) имеет вид

Вычислим теперь x-составляющую вектора ∆g :

65

Подставим теперь выражения (4.1.14) и (4.1.15) в x-компоненту уравнения (4.1.13). Окончательно получаем следующее уравнение:

Второе уравнение окончательной системы – это фурье-компо- нента уравнения (4.1.4).

Как видно, в полученную систему уравнений входят только х-компоненты скорости и магнитного поля.

Для начала рассмотрим случай идеальной плазмы, то есть устремим удельное сопротивление η к нулю. Тогда

При (k,H0 ), стремящемся к нулю, скорость обращается в бес-

конечность, то есть теория неприменима, и мы должны учитывать конечное сопротивление. Пусть поверхность x = 0 совпадает с по-

верхностью (k,H0 )= 0. Тогда вблизи этой поверхности можно

написать (k,H0 )≈ (k,H0 )′ x , где штрих означает производную по

x. Вдали от этой поверхности при большой проводимости можно пользоваться идеальной гидродинамикой и формулой (4.1.18). В этом случае (4.1.16) можно переписать так:

66

бранной нами системе координат kz = 0. Решение этой задачи известно:

Однако это решение терпит разрыв производной в точке x = 0 . Действительно, при x → +0

Следовательно, приближение идеальной МГД здесь неприменимо и надо вводить конечную проводимость. Будем называть эту область резистивной. Пусть ширина этой области 2L много меньше длины волны, α >> k . Тогда в уравнении (4.1.16) можно прене-

бречь величиной k2 в круглых скобках, и это уравнение перепишется так:

К этому уравнению добавляется уравнение (4.1.17) при k → 0:

67

Как уже указывалось, в этой узкой области величина (k,H0 ) практически линейно зависит от x, (k,H0 )≈ kH∞αx , где H∞ = H0x (x→∞) , и последним членом в (4.1.16) мы пренебрегли.

Разделим уравнение (4.1.23) на (k,H0 ) и проинтегрируем его по

Инкремент неустойчивости можно вычислить, подставляя это выражение в правую часть уравнения (4.1.26), а ∆′ – из (4.1.25) и пользуясь «приближением постоянного H», то есть, считая, что в

правой части (4.1.27) H1x ≈ H1x (x = 0)= const .

Качественно инкремент неустойчивости можно оценить так. В резистивной зоне

68

Тогда, считая в уравнении (4.1.23) оба члена в правой части о д- ного порядка, для оценки можно написать

Таким образом, условие устойчивости сводится к следующему:

∆′≥ 0.

Для того чтобы найти γ , надо оценить L . По порядку величины

В результате находим толщину резистивного слоя:

и выразим через него L:

69

1/5

( ′ )1/5 H

L = a S −2∆ a 0 2 . (4.1.37)

kH∞a

Окончательно

Напомним, что a – поперечный размер плазменного слоя. Как видно из полученного результата, инкремент тиринг-моды (резистивной неустойчивости) существенно меньше обратного альфвеновского времени, характерного для развития идеальных мод.

Теория похожей неустойчивости, так называемой неоклассической тиринг-моды, учитывает неоклассические эффекты.

4.2. Дрейфовая диссипативная неустойчивость

Вообще говоря, можно ожидать, что всевозможные отклонения от максвелловского распределения, в частности течения плазмы, могут приводить к неустойчивостям. В ловушках для удержания плазмы всегда имеются градиенты плотности и температуры, что вызывает течение плазмы. В этом разделе мы рассмотрим одну из таких неустойчивостей в столкновительном режиме. Она не способна разрушить плазменный шнур, так как локализована вблизи рациональной поверхности, но может дать вклад в аномальный перенос (см. также раздел 3.6).

Рассмотрим плоский слой плазмы в однородном магнитном поле Hz ≡ H0 , направленном вдоль оси z. В равновесии градиент дав-

ления направлен вдоль оси x. Скоростью частиц поперек магнитного поля, связанной с диффузией, и инерцией электронов можно пренебречь. Пренебрежем также стационарным электрическим полем и положим температуру ионов равной нулю. Тогда

а ток имеет только полоидальную составляющую j0 . В нулевом приближении имеем

70