Морозов Введение в теорию горячей плазмы Част2 2013

фазовом объёме d3pd3r. Элемент объёма dV выражается через сечение трубки и элемент её длины, dV = dlsS. Величина HdS=dΦ – это магнитный поток через площадку dS. При этом соотношение (3.1.7)

∫H 2 dl∫mf v||2 + 2 d3 p=nmddΦ∫H 2 dl v||2 + 2 . (3.1.8)

Вслучае почти изотропной функции распределения можно написать: δH δH

Среднеквадратичная скорость частиц в неподвижной плазме пропорциональна давлению:

Плазма будет устойчива, если её энергия при отклонении от положения равновесия будет возрастать, δQ>0, то есть

Во многих реальных системах давление анизотропно. Простейшим примером такой системы является пробкотрон. Вследствие ухода через магнитные пробки распределение частиц по параллельным скоростям отличается от распределения по перпендикулярным. В декартовой системе координат тензор давления диагонален и имеет вид

31

где

P =m2 ∫v2 fd3v=12(Pxx +Pyy ); P|| =Pzz =m∫v||2 fd3v ; f – функция

распределения частиц по скоростям.

В этом случае условие устойчивости (3.1.12) будет выглядеть так:

В токамаке продольное давление P|| мало отличается от перпендикулярного P . Согласно (1.1.5) должно выполняться равенство

так как в замкнутых системах величина dl не варьируется. Таким образом, условие устойчивости имеет вид

То есть интеграл ∫dlH должен убывать при удалении от оси систе-

мы.

Условие (3.1.15) можно представить несколько иначе:

где dS – сечение трубки, δV – объём трубки, а δΦ – магнитный поток через это сечение. Условием устойчивости является убывание объёма силовой трубки с ростом заключённого в ней магнитного потока.

32

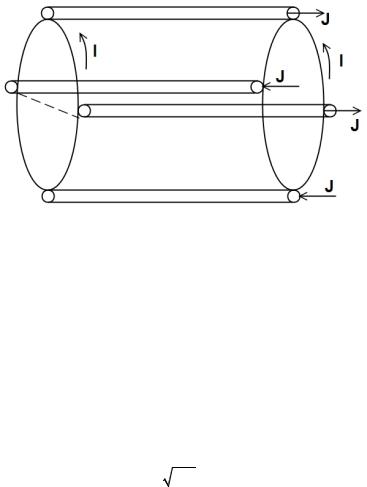
Очевидно, что невозможно создать систему с абсолютным минимумом магнитного потока. Но возможно создать систему с минимумом Н в среднем. Примерами таких систем являются цилиндр с эллиптическим сечением, в котором эллипс сечения вращается вокруг центральной оси, и пробкотрон со стабилизирующими стержнями (установка Иоффе, рис. 7).

Рис. 7. Схема установки Иоффе

Подробнее об этом можно прочитать в работе [1].

3.2. Неустойчивости цилиндрически симметричных плазменных конфигураций

В этом разделе мы рассмотрим неустойчивости идеальной плазмы, то есть будем пренебрегать диссипативными процессами. Такие неустойчивости наиболее опасны. Во-первых, они обычно занимают по радиусу всю область плазменного шнура. Во-вторых, время их нарастания чрезвычайно мало. Действительно, оно по порядку величина равно отношению радиуса плазменного шнура a к

установках составляет величину порядка 10-8 ÷ 10-7 с.

33

Рассмотрим вначале простейшую теорию неустойчивости цилиндрически симметричной конфигурации относительно цилиндрически симметричного возмущения, так называемой неустойчи-

вости относительно перетяжек, или «сосисочной неустойчивости». Пусть равновесная конфигурация представляет собой однородный плазменный цилиндр радиуса a. Пусть вдоль оси цилиндра, совпадающей с осью z, по поверхности цилиндра протекает ток J.

Цилиндр помещен в продольное магнитное поле Hz = const внутри плазмы и Hz = 0 вне её. Вне цилиндра (r ≥ a) существует полои-

дальное магнитное поле Hθ = 2crJ . Пусть теперь на плазменном ци-

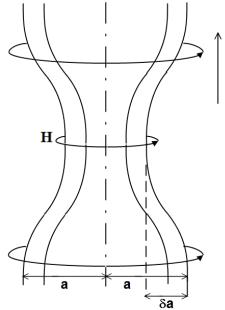
линдре образовалась перетяжка, радиус которой равен a −δa

(рис. 8).

Рис. 8. Неустойчивость относительно перетяжек

В силу идеальной проводимости поток магнитного поля через сечение перетяжки должен сохраниться:

34

Ток внутри шнура остался прежним, поэтому и циркуляция вектора Hθ также сохранилась, Hθa = (Hθ + δHθ )(a −δa), то есть

δHθ = δa .

Hθ a

Вне плазмы магнитное давление в первом по возмущению при-

ближении равно Hθ2 , а внутри – Hz2 . Газокинетическое давление

8π 8π

сохранилось. Поэтому равенство полных давлений по обе стороны границы плазмы в линейном приближении можно записать так:

Если давление внутри плазмы при образовании перетяжки выросло, то есть

то плазма устойчива, если наоборот, то неустойчива, и перетяжка будет развиваться.

3.3. Винтовая неустойчивость

Более общим случаем возмущений цилиндрической плазменной конфигурации является винтовое возмущение. Идеальную винтовую моду в иностранной литературе называют «kink mode». Будем в этом разделе следовать монографии [3].

Для анализа таких возмущений вернемся к достаточно общему уравнению (2.1.31). Напомним, что это уравнение описывает идеальную плазму, то есть плазму с бесконечной проводимостью. Как и в предыдущем разделе, градиент давления и ток в плазме (за исключением тока по поверхности) равны нулю. Такое распределение тока имеет место в пинчах:

35

Так как смещение ξ зависит от радиуса-вектора, волновой вектор является оператором,

Подставляя это выражение в (3.3.2) и учитывая, что divξ = 0, окончательно получаем

Умножим это уравнение скалярно на k . В силу ( 3.3.2) левая часть полученного равенства обращается в ноль. Правая часть обращается в ноль, если

Мы предположили, что ξ ~ exp(imθ), где m – целое число.

Общим решением уравнения (3.3.7) является линейная комбинация модифицированной функции Бесселя и функции Кельвина:

где С1 и С2 – произвольные постоянные. Функция Km расходится в

36

Подставим ξz (r) в радиальную компоненту уравнения (3.3.6), имея в виду, что радиальная составляющая волнового вектора яв-

Штрих означает производную по аргументу. Это решение должно быть «сшито» с решением в вакуумной области, где rotH = 0. Следовательно, магнитное поле может быть представлено как градиент некоторой функции ψ . Тогда уравнение divH = 0 перехо-

дит в уравнение Лапласа, решение которого снова имеет вид (3.3.8). Но во внешней области Im → ∞ при r → ∞ , поэтому С1 = 0.

В результате

На границе плазмы должно выполняться условие (2.1.38). При условии несжимаемости ( ,ξ)=0 оно приводится к виду

1 Заметим, что в соответствующих формулах (8.56) и (8.58) работы [3] содержатся опечатки.

37

Еще одно краевое условие – это обращение в ноль на границе тангенциальной составляющей электрического поля в системе отсчета, движущейся вместе с плазмой,

Берем rot от этого уравнения, учитываем, что в линейном приближении V = ∂∂ξt , и используем нормальную к границе составляющую

уравнения Максвелла rot(Et )= −1c ∂∂Htn . В результате получаем

Учитывая, что (k,ξ) = 0, это равенство можно переписать следующим образом:

Продифференцируем по радиусу (3.3.11) и подставим в левую

Подставляя (3.3.10) и (3.3.20) в (3.3.15), получаем в результате дисперсионное уравнение

Неравенство ω2 ≥ 0 является критерием устойчивости системы.

Поскольку Km′ < 0, второй член в правой части (так же, как и пер-

Km

38

вый) – стабилизирующий. Он имеет минимум, если множитель

(H0zi )2 > (H0θe )2 . Этот случай соответствует перетяжкам и уже был

рассмотрен в разделе 3.2.

Мода m =1, H0θe = 0 – это винтовая мода, «змейки» в русскоязычной литературе или «kink-mode» в англоязычной. Рассмотрим

В рассмотренном случае kz a <<1 второй член в скобках отрицателен, и плазма может быть неустойчивой.

Рассмотрим типичный для токамака случай H0ze >> H0θe . Снова

будем исследовать предел kz a <<1. Разложим в ряд функции Бесселя и Кельвина:

Im (x) ≈ Γ(m1+1) 2x m ;

Km (x) ≈ 12Γ(m) 2x m для m ≥1.

39

Здесь Γ(m) = (m −1)!; Γ(1) = Γ(2) =1.

Дисперсионное уравнение (3.3.21) в этом приближении имеет вид

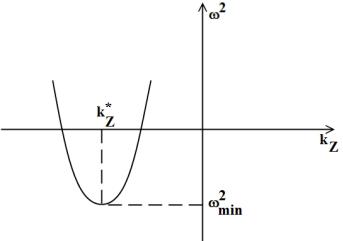
Квадрат частоты является квадратичной формой волнового вектора kz (рис. 9).

Рис. 9. Качественная зависимость квадрата частоты от kz

Значение ω = ωmin , соответствующее минимуму этой кривой,

определяет максимальный инкремент. Это достигается при значении kz = k* , когда парабола достигает минимума, т. е.

40