
Морозов Введение в теорию горячей плазмы Част2 2013
.pdf
ющих этому решению, являются цилиндрические поверхности, простирающиеся вдоль оси z′ от −∞ до +∞ . В этой области ч а- стицы удерживаться не могут.
б) ψ = 0 . В этом случае одно из решений представляет собой
точку в центре, а другое – эллипсоид, который является сепаратрисой, отделяющей замкнутые магнитные поверхности от разомкнутых.
Рис. 2. Сечение магнитных поверхностей сферомака плоскостью
ζ = const
в) ψ'> 0. Геометрическими местами точек, соответствующих
этому решению, является система вложенных тороидальных поверхностей. Эта область – область удержания плазмы.
Поверхность ψ'=1 вырождается в кольцо, соответствующее магнитной оси системы.
11
На рис. 2 представлено сечение системы поверхностей плоско-
стью ζ = const .
Итак, первым этапом расчёта системы для магнитного удержания плазмы является расчёт равновесия плазмы в магнитном поле. Уравнение Шафранова–Грэда – это статическое нелинейное уравнение. Во-первых, оно может быть обобщено на случай вращающейся плазмы. Во-вторых, оно нелинейное и, следовательно, допускает не единственное решение при одних и тех же граничных условиях.
1.2. Равновесие плазмы в токамаке
Ближе всего к параметрам термоядерного реактора в настоящее время находится токамак. Поэтому рассмотрим равновесие в такой системе подробно. Конфигурация его представляет собой тор с сильным продольным магнитным полем, вдоль которого течёт ток. В цилиндрическом приближении магнитные поверхности представляют собой коаксиальные цилиндры с постоянным радиусом. При свёртывании цилиндра в тор магнитные поверхности будут торами, оси которых будут смещены относительно магнитной оси. Рассмотрим такую тороидальную систему в приближении малой тороидальности. Отношение малого радиуса тора r к большому радиусу R обычно обозначают через ε . Будем рассматривать токамак в пределе малой тороидальности ε <<1. Сечение магнитных поверхностей плоскостью ζ = const в такой системе будет представ-
лять систему вложенных слегка вытянутых окружностей со смещёнными центрами. Будем считать, что эти сечения мало отличаются от окружностей радиуса r.
Для описания магнитных поверхностей введём новую систему координат r, ϑ, ζ . Старые цилиндрические координаты будем
называть r ', ζ, z . Удобно выбрать новую систему координат так,
чтобы поверхности r = const совпадали с магнитными поверхностями. Радиус поверхности r = const будем называть малым радиусом в отличие от большого радиуса R, равного расстоянию от центра сечения данной поверхности до оси симметрии тора (рис. 3).
12
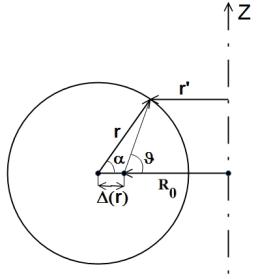
Пусть R0 – большой радиус магнитной оси системы. Тогда центр магнитной поверхности радиуса r будет удален от оси симметрии тора на расстояние
R = R0 + ∆(r). |
(1.2.1) |
Рис. 3. Квазицилиндрическая система координат
Введем точку А на окружности r = const . Радиус r ' точки А в старой системе координат в новой системе координат выражается следующим образом:
r '= R − r cosα . |
(1.2.2) |
Угол α = ϑ+ δ показан на рис. 3. В случае малой тороидальности он мало отличается от азимутального угла ϑ. Тороидальное магнитное поле в этом случае можно представить как
Hζ = H0 (1+εcosα)≈ H0 (1+εcosϑ). |
(1.2.3) |
Азимутальное магнитное поле в том же приближении может быть представлено в виде
Hϑ = Hϑ0 ((1+ Λ(r)cosϑ), |
(1.2.4) |
где Λ(r)– параметр асимметрии, зависящий от распределения тока и давления.
13
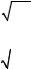
В новой цилиндрической системе координат квадрат элемента
длины dl2 = dr'2 + r'2 + dz2 |
будет иметь вид |
dl2 = gik dxi dxk . |
(1.2.5) |
Здесь dxi – контравариантные компоненты вектора dl, gik – метрический тензор, отличные от нуля компоненты которого с точностью до ε имеют вид
g =1− 2 |
d∆ |
cosϑ; |
|
|
(1.2.6) |
|||||
|
|
|
||||||||
11 |
|
|
|
dr |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
g12 |
= r |
d∆ |
sinϑ+ r |
∂δ |
; |
(1.2.7) |
||||
|
dr |
|
||||||||
|
|
|
|
|
|
∂r |
|
|
||
g22 |
= r |
2 |
|
|
|
∂δ |
|
|
(1.2.8) |
|
|
1+ 2 |
; |
|
|
||||||
|
|
|
|
|
|
∂ϑ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|||
g33 = R0 |
1− |
2 |
|
|
|
cosϑ . |
|
|
|
(1.2.9) |
||||||||||||||
R0 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение силовых линий в ковариантном виде выглядит как |
||||||||||||||||||||||||
dϑ |
= |
H |
(2) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(1.2.10) |
|||||||
dζ |
H |
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
Hϑ |
|
|
|
1 |
0 |
|
|
|
|
∂δ |
|
||||||
H |
|
|
|
= |
|
|
|
|
|
|
|
= |
|
r |
Hϑ |
1+ Λcosϑ− |
; |
(1.2.11) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
g22 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ϑ |
|
|||||
|
(3) |
|
|
|
|
|
Hζ |
|
|
|
1 |
|
|
|
|
|
2r |
|
|
|
||||
H |
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
H0 |
1+ |
|
cosϑ . |
(1.2.12) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|||||||||||
|
|
|
|
|
|
|
|
|
g33 |
|
|
R0 |
|
|
|
|
|
|||||||
Величину δ |
удобно выразить так, чтобы силовые линии были |
|||||||||||||||||||||||
прямыми, то есть выполнялось бы условие |
|
|||||||||||||||||||||||
∂δ |
= |
|
H |
(2) |
= const . |
|
|
|
|
|
(1.2.13) |
|||||||||||||
∂ϑ |
|
H |
(3) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для этого должно выполняться равенство |
|
|||||||||||||||||||||||
∂δ |
|
|
|
|
|
|
2r |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
|
1− |
sinϑ. |
|
|
|
|
|
(1.2.14) |
|||||||||||||||
∂ϑ |
|
R0 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Действительно, подставив это выражение в (1.2.11) и разделив на H (3) , находим
14
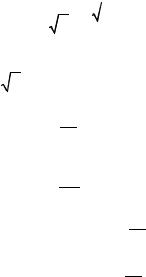
H (2) |
|
R H 0 |
|
|
|
|
|
|
||||||||
H (3) |
= |
0 |
|
|
ϑ = const. |
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
r H0 |
|
|
|
|
|
|
||||||||
Из условия |
|
|
|
|
|
|
|
|
|
|||||||
divΗ = |
1 |
|
∂ |
|
|
|
|
= 0, |
||||||||
|
|
gH(2) |
||||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
g ∂ϑ |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где g = Detgik |
, находим |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
g = R0r 1− 2 |
cosϑ |
; |
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
R0 |
|
|
|||||
Λ = d∆ + r . dr R0
Окончательно для метрического тензора получаем g11 =1− 2ddr∆ cosϑ;
g12 = ddr2∆2 r2 + ddr∆ − Rr2o sinϑ;
g22 = r2 1+ 2 ddr∆ − Rr0 cosϑ ;
2 |
|
|
r |
|
|
g33 = R0 |
1 |
− 2 |
|
cosϑ . |
|
R0 |
|||||
|
|
|
|
(1.2.15)
(1.2.16)
(1.2.17)
(1.2.18)
(1.2.19)
(1.2.20)
(1.2.21)
(1.2.22)
В этой системе координат, как уже указывалось, силовые линии являются прямыми и описываются выражениями
ϑ = |
H 0R |
ζ + const = |
ζ |
+ const. |
(1.2.23) |
|
ϑ |
0 |
|
||||
rH0 |
|
q(r) |
||||
|
|
|
|
|
||
Ковариантные и контравариантные компоненты магнитного поля имеют вид
H
H
(i)
(i)
|
0 |
|
d |
2 |
∆ |
|
d∆ |
|
|
r |
|
|
|
0 |
|
|
d∆ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
; |
||||||||||||
= Hϑ |
dr2 |
r + dr |
− |
|
sinϑ;rHϑ |
1+2 dr cosϑ ; R0H0 |
|
||||||||||||||||
R |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
H |
0 |
|
|
|
r |
|
|
|
|
H |
|
|
|
r |
|
|
|
|
|
||
|
|
ϑ |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||
= 0; |
|
|
1 |
+ 2 |
|
|
cosϑ ; |
|
1+ 2 |
|
|
cosϑ . |
|
|
|||||||||
|
r |
|
|
R |
|
R |
|
R |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|||||
(1.1.24)
(1.2.25)
15
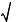
Составляющая H(3) будет содержать еще малую добавку δH(3) к
R0H0 , возникающую из-за азимутального тока. В результате электрический ток выражается следующим образом:
|
(i) |
|
c |
|
(i) |
|
|
(2) |
|
c |
|
∂H(2) |
|
∂H(1) |
|
|
|
j |
|
(rotH) |
|
j |
|
|
|
|
|
||||||||
|
= |
|
|
= 0; |
|
; |
|
|
|
|
− |
|
. |
(1.2.26) |
|||
|
4π |
|
|
|
|
∂r |
∂ϑ |
||||||||||
|
|
|
|
|
|
|
|
|
4π g |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя ток в уравнение равновесия в нулевом по ε приближении получаем
|
IHϑ |
= 4π dP0 + |
Hϑ |
|
d |
(rHϑ0 ). |
|
|
|
|
|
(1.2.27) |
|||||||
|
cR |
r |
|
dr |
|
|
|
|
|
||||||||||
|
|
dr |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В следующем приближении имеем |
|
|
|
||||||||||||||||
|
d |
|
2 |
|
|
r2 |
2 |
|
|
r2 |
dP |
|
|
r |
|
|
|
||
|
|
rHϑ |
Λ − |
|
|
Hϑ |
= |
8π |
|
|
− |
|
|
|
, |
(1.2.28) |
|||
|
dr |
R |
R |
dr |
|
R H2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
ϑ |
|
|
|||
откуда простым интегрированием находим Λ . |
|
||||||||||||||||||
Здесь для простоты опущен индекс «0» у H и P. |
∆ обращается в |
||||||||||||||||||
Если положить, что на кожухе |
(r = b) сдвиг |
||||||||||||||||||
ноль, можно написать |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
b |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ = −∫ |
Λ − |
|
|
dr. |
|
|
|
|
|
|
|
|
(1.2.29) |
||||||
|
R |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
r |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Эта величина называется смещением Шафранова.
ГЛАВА 2. ГИДРОДИНАМИЧЕСКИЙ ПОДХОД К ОПИСАНИЮ НЕУСТОЙЧИВОСТЕЙ
Рассмотрим общие подходы к проблеме устойчивости. Один из таких подходов – метод малых возмущений. Вначале рассматривается равновесие плазмы. Затем вводится малое отклонение от этого равновесия. Если при этом малое возмущение нарастает со временем, такое равновесие является неустойчивым.
В этой главе мы рассмотрим два метода анализа устойчивости: метод малых возмущений и энергетический принцип. Оба рассмотренных здесь метода имеют ограниченные области применимости. В одножидкостном приближении они позволяют анализировать довольно широкий класс желобковых и винтовых мод, весьма важный при анализе устойчивости тороидальных систем. С другой
16
стороны, за рамками рассмотрения оказываются возмущения, связанные с разделением зарядов, такие, как ленгмюровские моды, а также коротковолновые возмущения. Последние требуют кинетического описания. Заметим также, что метод малых возмущений может быть развит и в многожидкостной гидродинамике, и в кинетике.
2.1. Метод малых возмущений
Метод малых возмущений мы будем рассматривать в гидродинамическом приближении Брагинского [2]:
∂ne |
|
+ div (ne Ve )= 0; |
|
|
|
|
|
|
|
|
|
|
|
(2.1.1) |
|||||
∂t |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∂ni |
|
+ div (ni Vi )= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
(2.1.2) |
||||
∂t |
|
= − P − e n |
|
|
|
|
|
|
|||||||||||
∂ |
|
|
|
|
|
|
|
|
|
|
|||||||||
m n |
+(V , ) |
V |
[V |
,H]− n eE + R |
|
−F |
; (2.1.3) |
||||||||||||
|
|
T |
|||||||||||||||||
e e |
e |
|
e |
|
e |
c |
|
e |
|
e |
e |
|
e |
||||||
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
mn |
∂ |
+(V, ) V |
= − P + e n |
[V |
,H]+ neE – R |
|
– F . |
(2.1.4) |
|||||||||||
|
|
T |
|||||||||||||||||
i i |
|
i |
|
i |
|
c |
i |
|
i |
|
i |
|
i |
|
|||||
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь Fe,I |
– вязкие силы, R – сила трения между электронами и |
||
ионами. Остальные обозначения – стандартные. |
|
||
Будем |
предполагать |
квазинейтральность плазмы, |
то есть |
ne = ni ≡ n . Ведем массовую скорость |
|
||
V = (meVe + mi Vi ) (me |
+ mi ). |
(2.1.5) |
|
Умножая уравнения (2.1.1) и (2.1.2) на массы электронов и ионов соответственно и суммируя два этих выражения, получаем уравнение непрерывности для плазмы как целого:
∂ρ |
+ div(ρV )= 0. |
(2.1.6) |
∂t |
|
|
Сложим уравнения (2.1.3) и (2.1.4). Пренебрегая вязкими членами, получаем
ρ |
d |
V = − P+ |
1 |
[j,H]. |
(2.1.7) |
|
dt |
c |
|||||
|
|
|
|
17

Здесь P = Pe + Pi , |
d |
= |
∂ |
+(V, ). Во многих задачах |
инерция |
|
dt |
∂t |
|||||
|
|
|
|
|||
электронов пренебрежимо мала. Поэтому положим me = 0 |
в урав- |
|||||
нении (2.1.3). Ток j можно выразить через электронную и ионную скорости:
J = ne(Vi – Ve). (2.1.8)
Полагая, что скорость электронов не слишком велика по сравнению со скоростью ионов (это предположение не всегда справедливо), можно положить также V ≈ Vi .
Для анализа таких гидродинамических неустойчивостей, как винтовая неустойчивость в токамаке, которые развиваются за времена, много меньшие времени между столкновениями, можно пренебречь столкновениями, то есть силами трения между электронами и ионами. В этом случае уравнение (2.1.3) примет вид
|
1 |
|
P + E + |
1 (V − j |
( |
ne |
) |
,H = 0 . |
(2.1.9) |
||||||
|
|
|
|
||||||||||||
|
en |
e |
c |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Здесь мы пренебрегли инерцией электронов. |
|
||||||||||||||
Член [j, H] выразим с помощью уравнения (2.1.7). |
|
||||||||||||||
mn |
d |
|
V = − P + neE + ne |
[ |
V,H |
] |
. |
(2.1.10) |
|||||||
|
|||||||||||||||
i dt |
i |
|
c |
|
|
|
|
|
|
|
|||||
Левую часть уравнения (2.1.10) можно оценить как mτi n V, где τ – характерное время развития неустойчивости, а её отношение к
последнему члену в правой части – как (ωHi τ)−1. Здесь ωHi = eH – mic
ионная ларморовская частота. Таким образом, для процессов, характерное время развития которых много больше ионной ларморовской частоты, левую часть уравнения (2.1.10) можно положить равной нулю.
Сравним теперь первый и последний члены в (2.1.10). Для первого члена можно сделать такую оценку:
P ~ |
nT |
nm v2 |
(2.1.11) |
i ~ |
i Ti . |
||
i |
a |
a |
|
|
|
Последний член в правой части (2.1.10) можно оценить следующим образом:
18

|
ne [V,H] |
|
V ωHi nmi [V,H]. |
(2.1.12) |
||||
|
||||||||
|
c |
|
|
|
|
|
|
|
Отношение двух этих членов можно представить в виде |
|
|||||||
|
v2 |
= |
ρ |
|
|
v |
|
|
|
Ti |
|
i |
Ti |
. |
|
||
|
aV ωHi |
|
a |
V |
|
|
||
Здесь ρi – ионный ларморовский радиус. Если отношение макроскопической скорости плазмы к её тепловой скорости достаточ-
но велико (оставаясь малым по сравнению с единицей), V >> ρi , vTi a
то в уравнении (2.1.10) можно пренебречь также и градиентом давления. В результате получаем
E + |
1 [V,H] = 0. |
|
(2.1.13) |
|
|
|
c |
|
Pρ−γ = const |
В качестве уравнения энергии возьмем адиабату |
||||
или |
|
|
|
|
|
∂ |
+(V, ) Pρ−γ = 0, Pρ−γ =0. |
=0. |
(2.1.14) |
|
||||
∂t |
|
|
|
|
К материальным уравнениям необходимо добавить уравнения
Максвелла: |
1 ∂ |
|
|
|||
rotE = − |
H ; |
(2.1.15) |
||||
|
|
|||||
c ∂t |
||||||
|
|
|
|
|||
div H = 0; |
|
(2.1.16) |
||||
rot H = |
4π |
j. |
|
(2.1.17) |
||
|
|
|||||
|
|
c |
|
|
||
В последнем уравнении опущена производная по времени от электрического поля, то есть полученная система уравнений не описывает такие быстрые процессы, как распространение радиоволн в плазме.
Как всегда в методе малых возмущений, ищем все величины в виде суммы, не зависящей от времени невозмущенной величины и
малой добавки, H = H0 + H1; P = P0+P1; ρ = ρ0 +ρ1 ; E = E1; V = 6. Мы предположили, что невозмущённые значения скорости и элек-
трического поля равны нулю.
19

В нулевом приближении получаем |
|
||||||||||||
(ρ0V0 )= 0; |
|
(2.1.18) |
|||||||||||
P0 = 1 |
[j0,H0 ]; |
|
(2.1.19) |
||||||||||
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
( ,H0 )= 0; |
|
|
(2.1.20) |
||||||||||
[ ,H0 ]= |
4π |
j0 . |
|
(2.1.21) |
|||||||||
c |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
В первом приближении |
|
|
|||||||||||
|
∂ρ1 + |
(ρ0,V0 )= 0; |
|
(2.1.22) |
|||||||||
|
∂t |
∂ |
|
+ P1 = 1[j0,H1]+ |
1[j1,H0 ]; |
|
|||||||
ρ0 |
V1 |
(2.1.23) |
|||||||||||
|
|
||||||||||||
|
∂ |
|
∂t |
|
|
|
|
c |
c |
|
|||
|
P1 +(V, P0 )+ γP0 ( ,V0 )= 0; |
(2.1.24) |
|||||||||||
|
∂t |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
∂H1 |
= rot[V,H0 ]; |
|
(2.1.25) |
|||||||||
|
|
|
|||||||||||
|
∂t |
|
4π |
|
|
|
|
||||||
rotH = |
|
j . |
|
(2.1.26) |
|||||||||
|
|
|
|||||||||||
|
|
|
1 |
|
c |
1 |
|
|
|||||
Удобно ввести смещение элемента плазмы V = dtd ξ ≈ ∂∂t ξ . По-
следнее равенство получено в первом порядке теории возмущений путем отбрасывания квадратичного по возмущению члена. Уравнение (2.1.25) теперь перепишется следующим образом:
∂H |
|
|
∂ |
ξ,H0 |
|
|
|
|
1 |
= rot |
|
. |
(2.1.27) |
||
∂t |
∂t |
||||||
|
|
|
|
|
|||
Интегрируя это уравнение по времени, получаем |
|
||||||
H1 = rot[ξ,H0 ]. |
|
(2.1.28) |
|||||
Аналогичным образом получаем |
|
||||||
ρ1 = − (ρ0ξ); |
|
(2.1.29) |
|||||
P1 = −( P0,ξ)− γP0 ( ,ξ). |
(2.1.30) |
||||||
Окончательно, подставляя полученные выражения в уравнение (2.1.23), получаем уравнение второго порядка для ξ:
20
