
Морозов Введение в теорию горячей плазмы Част2 2013
.pdfМы будем рассматривать чисто электростатические возмущения, то есть пренебрегать возмущениями магнитного поля. Тогда уравнение движения плазмы приобретает вид
mi ndV |
= − P1 |
+ |
1 |
[j1,H0 ]. |
(4.2.3) |
dt |
|
|
c |
|
|
Обобщенный закон Ома дается выражением (5.4.6) [8]:
1 |
P + E + |
[Ve ,H0 |
] |
= ηj . |
(4.2.4) |
|
|
|
|||
ne |
e |
c |
|
|
|
|
|
|
|
Здесь η =1/ σ – удельное сопротивление. Мы пренебрегли термосилой и вязкостью. С учётом соотношений j = en(V − Ve ) и (4.2.1) можно написать:
1 |
P− φ+ |
[V,H0 |
] |
= ηj + |
[j1, H0 |
] |
. |
(4.2.5) |
ne |
c |
|
nec |
|
||||
|
|
|
|
|
|
Мы ввели скалярный потенциал E = − ϕ . Кроме того, нам по-
надобятся уравнения непрерывности для вещества и электрического тока:
|
∂n1 |
+ div(n0V)= 0 |
(4.2.6) |
|
∂t |
||
|
|
|
|
и |
|
|
|
divj = 0. |
(4.2.7) |
||
В фурье-представлении по времени уравнения (4.2.3) и (4.2.5) выглядят так:
−iωmi n0V = −Te n1 + |
1[j1,H0 ]; |
(4.2.8) |
|||||
Te n1 − ϕ+ [V,H0 ] |
c |
[j1, H0 ]. |
|
||||
= ηj + |
(4.2.9) |
||||||
|
n e |
|
c |
|
|
nec |
|
|
0 |
|
|
|
|
|
|
Выразим [j1,H0 ] из уравнения (4.2.9) и подставим в (4.2.8): |
|||||||
i |
ωm |
V = ϕ− |
[V,H0 |
] |
+ ηj . |
|
(4.2.10) |
e |
c |
|
|
||||
|
|
|
|
|
|
||
Все параметры равновесного состояния не зависят ни от y, ни от z. Поэтому возмущённые параметры можно разложить в интеграл Фурье по y и z. Тогда z-компоненту тока можно найти из уравнения
(4.2.9):
71
|
ikz |
|
Te |
|
|
|
|
jz = |
|
n1 |
−ϕ . |
(4.2.11) |
|||
|
|
||||||
|
η n0e |
|
|
|
|||
В уравнения (4.2.10) можно опустить член ηj . Соответствую-
щие компоненты этого уравнения имеют вид |
|
||||||||||||||||||
i ωmi |
V |
|
= |
∂ϕ |
− |
H0 |
V |
|
|
|
|
(4.2.12) |
|||||||
|
∂x |
|
|
|
|
|
|
|
|
||||||||||
e |
x |
|
|
|
|
|
c |
|
|
|
y |
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i ωmi V |
y |
|
= ik |
ϕ+ H0 V . |
|
(4.2.13) |
|||||||||||||
e |
|
|
|
y |
|
|
|
|
|
|
c |
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Разрешая эти два уравнения относительно Vx и Vy, получаем |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω ∂ϕ |
|
|
|||
|
|
|
|
|
|
kyϕ− |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
c |
|
ωHi |
|
|
|||||||||||
V = −i |
|
|
|
|
|
|
|
|
∂x |
; |
(4.2.14) |
||||||||
H0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||
x |
|
|
|
|
|
|
|
ω |
|
|
|
|
|||||||
|
|
|
|
|
|
|
1− |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
ωHi |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∂ϕ |
|
|
ω |
kyϕ |
|
|
|
|||||||
|
|
c |
|
|
∂x − |
|
|
|
|
|
|
||||||||
Vy = |
|
|
ωH |
. |
|
(4.2.15) |
|||||||||||||
H0 |
|
|
|
|
ω |
2 |
|
|
|
||||||||||
|
|
|
|
|
1− |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ωH |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Здесь |
ωHi |
= eH0 |
|
– ионная циклотронная частота. Для дрейфо- |
|||||||||||||||
|
|
|
|
|
|
|
mi c |
|
|
|
|
|
|
|
|
||||
вой диссипативной моды можно положитьω<< ωHi . Поэтому членами, квадратичными по ω/ ωHi , можно пренебречь,
Найдём теперь остальные компоненты возмущённого тока. Перпендикулярная составляющая уравнения (4.2.9) при пренебрежении членом, пропорциональным сопротивлению плазмы, даёт
|
− φ+ |
1[V,H |
0 |
] en = −T |
n |
+ |
1[j,H |
0 |
], |
(4.2.16) |
||||
|
|
c |
|
|
0 |
e |
1 |
c |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
что в компонентах приобретает вид |
|
|
|
|||||||||||
|
|
|
c |
|
|
ω ∂ϕ |
|
cTe |
|
|
|
|
|
|
|
jx = i |
en0 |
|
|
− ky |
n1 |
; |
|
|
(4.2.17) |
||||
|
H0 |
|
ωHi |
∂x |
|
|
||||||||
|
|
|
|
H0 |
|
|
|
|
|
|||||
72

|
j |
|
= cTe ∂n1 |
−en |
ω c |
|
k |
ϕ . |
(4.2.18) |
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
y |
|
H0 ∂x |
|
0 ωHi H |
0 |
y |
|
divj = 0 и будем |
||||||||
Подставим выражения для тока в уравнение |
||||||||||||||||||
считать, что k 2 |
>> |
∂2ϕ |
. В результате получим |
|
||||||||||||||
∂x2 |
|
|||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|||
|
kz2 |
T |
n1 |
+ i en0c |
|
ω |
k 2 |
− kz2 ϕ = 0. |
(4.2.19) |
|||||||||
|
|
|
|
|
|
|||||||||||||
|
eη |
e |
|
n0 |
|
H0 ωHi |
|
|
|
y |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
η |
|
||||||||
Ещё одно уравнение получим с помощью уравнения непрерывности ∂∂nt1 + div(n0V )= 0. Из z-компоненты уравнения (4.2.8) находим
V = |
ekz |
ϕ. |
(4.2.20) |
|
|||
z |
miω |
|
|
|
|
|
Подставляя (4.2.14), (4.2.15) и (4.2.20) в уравнение непрерывности, получаем
n |
|
c |
|
|
ky2 |
|
ω |
|
k2 |
|
ky |
dn |
|
|
||
1 |
+ |
|
|
|
|
|
− |
|
Hi |
z |
+ |
|
|
0 |
. |
(4.2.21) |
n |
H |
|
ω |
|
|
n |
|
|||||||||
|
0 |
|
H |
|
ω2 |
|
ω dx |
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
Определитель системы уравнений (4.2.19) и (4.2.21) даёт дисперсионное уравнение для дрейфовой диссипативной моды:
i |
en c |
|
ω |
k2 |
=T |
|
k2c |
|
|
ky2ω |
− |
k |
2 |
ω |
Hi |
+ k |
|
|
1 dn |
|
= 0 |
|||||||||||||||||||
|
0 |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
0 |
|
|||||||||||||||
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
||||||||||||||||||||
|
|
H |
0 |
Hi |
|
y |
|
|
e eηH |
0 |
|
ω |
Hi |
|
|
|
|
|
|
y n dx |
|
|
||||||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
2 ω |
|
H |
|
|
|
|
|
|
|
2 |
|
|
1 miTeky |
|
|
|
|
dn |
|
|
|
|||||||||||||
|
ω2 |
+i |
k |
|
|
|
−i |
k |
|
|
1 |
|
= 0. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
0 |
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||||||||||
|
ω |
2 |
k |
|
ω |
|
|
en cη |
k |
2 |
n η eH |
|
|
|
|
|
||||||||||||||||||||||||
|
Hi |
|
|
y |
|
Hi |
|
|
|
|
y |
e |
0 |
|
n dx |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||
Это выражение можно представить также в виде
ω2 |
|
k2 |
ω |
|
|
H |
|
|
|
|
|
cT |
|
|
ky2 |
|
cT |
|
ω |
|
|
|
|||||
|
|
+i |
z |
|
|
|
|
|
|
0 |
|
− |
1 |
+ |
e |
|
|
|
− |
e |
|
Hi |
+ |
||||
ω2 |
|
|
|
k2 |
ω |
Hi |
|
en cη |
|
|
|
eH |
0 |
|
ω |
Hi |
|
eH |
0 |
ω2 |
|
|
|||||
Hi |
|
y |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+i |
k 2 |
|
Teky |
|
|
1 |
dn |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
k2 |
e2n cηω |
Hi |
|
n |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(4.2.22)
(4.2.23)
(4.2.24)
В этом выражении в скобках можно пренебречь двумя последними членами по сравнению с единицей.
73

Введем дрейфовую частоту |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
ω = − |
cTe |
|
|
1 |
dn0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.2.25) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
* |
|
|
|
|
eH |
0 |
|
|
n |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Умножим уравнение (4.2.24) на ωHi 2 |
. В результате дисперси- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω* |
|
|
|
|
|
||||
онное уравнение приобретает вид |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
ω2 |
+i |
m |
|
k 2 ω2 |
|
|
ω |
−i |
m k 2 ω2 |
|
|
= 0. |
|
|
|
|
(4.2.26) |
||||||||||||||||||||||
2 |
|
|
|
i |
|
|
|
2 |
|
|
|
|
Hi |
|
|
|
i |
|
2 |
|
Hi |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||||||||
ω |
|
|
|
m k |
y |
ω ν |
ei |
|
ω |
|
m k |
y |
ω ν |
ei |
|
|
|
|
|
|
|
||||||||||||||||||
* |
|
|
|
|
|
|
e |
|
|
|
|
* |
|
|
* |
|
|
e |
|
* |
|
|
|
|
|
|
|
||||||||||||
Введём |
|
|
безразмерную |
|
частоту |
|
ω= |
ω |
и |
обозначение |
|||||||||||||||||||||||||||||
|
|
|
|
ω |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
Ω = kz2 |
|
mi |
|
ω2Hi |
|
> 0. |
|
Тогда |
дисперсионное |
уравнение принимает |
|||||||||||||||||||||||||||||
k 2 |
|
m ω ν |
ei |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y |
|
|
|
e |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
совсем простой вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ω2 +iωΩ −iΩ = 0, ω = −i |
Ω |
|
|
|
Ω2 |
+iΩ . |
|
|
(4.2.27) |
||||||||||||||||||||||||||||||
2 |
± |
|
− |
4 |
|
|
|
||||||||||||||||||||||||||||||||
Рассмотрим |
|
|
случай |
|
ky2 >> kz2 . |
|
Для |
таких |
возмущений |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Imω ≈ ± |
|
2 |
|
|
|
|
|
|
|
|
или в размерном виде |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
kz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Imω= ± |
|
|
|
2 |
|
|
|
ω |
Hi |
ω* |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.2.28) |
||||||||||||||
|
|
2 |
|
|
|
ky |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νei |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Как видно, решение со знаком «плюс» соответствует неустой-
чивости. |
|
|
получаем |
|
В противоположном случае, ky2 << kz2 |
||||
Imω = |
1 |
; Imω = −Ω , |
(4.2.29) |
|
Ω |
||||
1 |
2 |
|
||
то есть одно из решений устойчиво, а другое слабо, неустойчиво.
74
ГЛАВА 5. ЭЛЕМЕНТЫ ТЕОРИИ ПЕРЕНОСА ТЕПЛА И ЧАСТИЦ
Проблема переноса тепла и частиц является одной из важнейших в проблеме термоядерного синтеза. Действительно, выход термоядерной энергии должен превосходить потери тепла. Это возможно лишь при достаточно высокой температуре, когда термоядерная реакция идет достаточно интенсивною. К сожалению, теория переноса в настоящее время далека от завершения. Эксперимент показывает, что потери тепла и частиц существенно превосходят те, что предсказывает классическая теория. При этом, если переносы по ионному каналу не слишком сильно отличаются от теоретических (так называемых неоклассических), то потери по электронному каналу обычно на порядок–два превышают неоклассические. Поэтому для расчётов термоядерных установок обычно пользуются эмпирическими скейлингами. В этой главе мы рассмотрим простейшую задачу переносов в прямом магнитном поле и так называемую неоклассическую теорию, базирующуюся на классических представлениях, но учитывающую особенности переносов в тороидальной геометрии.
5.1. Классическая теория переноса
В этом разделе мы рассмотрим классические, то есть не учитывающие тороидальных эффектов и турбулентности переносы в плазме. Уравнение непрерывности, описывающее переносы в направлении, перпендикулярном магнитным поверхностям, имеет вид
∂n |
+ div(nV)= 0. |
(5.1.1) |
∂t |
|
|
Пока мы не конкретизировали вида перпендикулярной скорости отдельной частицы, такое уравнение описывает как классические переносы, так и аномальные. Будь то длина пробега в незамагниченной плазме, или ларморовский радиус в замагниченной, или расстояние, на которое частица переносится благодаря однократному взаимодействию с волной, если эта величина много меньше характерного размера задачи, например малого радиуса плазмы в
75

токамаке, то такой перенос носит диффузионный характер. Поток плазмы, перпендикулярный магнитному полю, Γ = nV , пропор-
ционален коэффициенту диффузии D. В одномерном случае в о т- сутствие источников можно написать
∂n |
|
∂ |
∂n |
|
|
|
∂t |
− |
|
D |
|
= 0. |
(5.1.2) |
|
||||||
|
∂x |
∂x |
|
|
||
По порядку величины запишем |
|
|||||
D |
(∆x)2 |
, |
(5.1.3) |
|
τ |
||||
|
|
|
||
где ∆x |
– длина пробега между столкновениями, а τ |
– время между |
||
ними. В спокойной замагниченной плазме для частиц сорта j роль ∆x играет ларморовский радиус ρ j , а роль τ – обратная частота
кулоновских столкновений νjk = τ−1 частиц сорта |
j с частицами |
сорта k , и по порядку величины имеем |
|
D ≈ ρ2j νjk . |
(5.1.4) |
Классический коэффициент диффузии можно более точно выразить через частоту столкновений. Для этого рассмотрим стационарное уравнение импульса для частиц сорта j , сталкивающихся с
частицами сорта k :
− Pj + z jcen [V,H]+ nzj eE − mj nνjk u jk = 0 .
Здесь u jk = Vj − Vk . Умножая это уравнение на H раскрывая двойное векторное произведение, получаем
|
|
c |
|
|
|
H, P |
|
|
c |
|
|
|
|
|
ν |
jk |
|
u |
jk |
,H |
|||||
v |
= |
|
|
|
|
j |
+ |
|
[E,H]− |
|
|
|
|
|
|
|
; |
||||||||
nz j e |
|
|
|
|
H 2 |
H |
|
ωHj |
|
|
H |
|
|
||||||||||||
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
c |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v(0) = |
|
|
|
H, Pj |
|
+ |
|
[E,H]. |
|
|
|
|
|
|
|
|
|
|
|||||||
nz j e |
|
|
|
|
H 2 |
|
H |
|
|
|
|
|
|
|
|
|
|
|
|||||||
jk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В первом приближении получаем |
|
|
|
|
|
|
|
|
|||||||||||||||||
(1) |
νjk |
|
0 |
0 |
|
|
|
νjk |
(Pj + Pk |
) |
|
|
|||||||||||||
H, v j − vk |
|
|
|
|
|
||||||||||||||||||||
v j = |
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
. |
|
|
ωHj |
|
|
|
|
H |
|
|
|
|
2 |
|
|
|
mj n |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
ωHj |
|
|
|
|
|
|
|
|||||||
(5.1.5)
векторно и
(5.1.6)
(5.1.7)
(5.1.8)
76
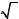
Рассмотрим случай, когдаTj =Tk ≡T
(1) |
νjk |
2T n |
2 |
n |
. |
(5.1.9) |
vj = − |
|
|
= −νjk ρj |
|
||
2 |
mj n |
n |
||||
|
ωHj |
|
|
|
Поток частиц в направлении, перпендикулярном магнитному полю, пропорционален плотности и не зависит от сорта частиц
Γj = −νjk ρ2j n = −Dj n. |
(5.1.10) |
Действительно, из третьего закона Ньютона mj νjk = mk νkj , квад-
рат ларморовского радиуса пропорционален массе частицы, а коэффициент диффузии D = νjk ρ2j от неё не зависит. Таким образом,
классическая диффузия автоматически амбиполярна, Γe = Γi .
5.2. Неоклассическая теория переноса
В тороидальном случае классическая теория претерпевает существенные изменения, которые радикальным образом зависят от частоты столкновений. Рассмотрим сначала так называемый банановый режим.
Банановый режим
Это случай, когда обратная частота столкновений много больше периода обращения запертых частиц по банану ([8]).
Смещение пролётных частиц по радиусу мало отличается от ларморовского радиуса. Запертые частицы смещаются по радиусу на существенно большее расстояние:
∆rj ≈ ρj |
q |
. |
(5.2.1) |
|
|
|
|||
|
|
|
||
|
|
ε |
|
|
И хотя этих частиц в ε−1/2 раз меньше, их вклад в переносы оказывается определяющим.
Меняется также и эффективное время между столкновениями. В классическом случае это время, за которое скорость частицы в результате множества далеких столкновений повернётся в среднем на угол порядка π / 2. При этом она сместится на величину порядка ларморовского радиуса. В тороидальном случае пролётная частица, превратившись в запертую, сместится на величину порядка
77
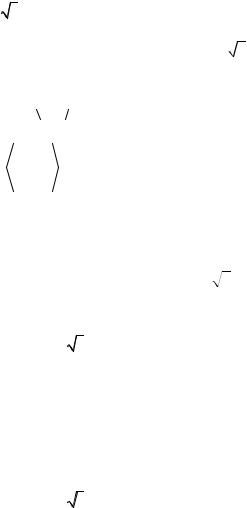
∆rj ~ ρj |
q |
|
. Запертая частица превращается в пролётную, если её |
|
|
|
|
||
|
ε |
|||
|
|
|
|
|
скорость, первоначально направленная почти поперёк магнитного
поля, должна повернуться на угол порядка 
 ε . Случайное рассея-
ε . Случайное рассея-
ние на малые углы в результате столкновений аналогично броуновскому движению, когда средний квадрат смещения пропорциона-
лен времени,  ∆x2
∆x2  ~ t. Аналогичное соотношение можно написать и для угла поворота скорости частицы:
~ t. Аналогичное соотношение можно написать и для угла поворота скорости частицы:
|
|
v 2 |
|
||
δα2 ≈ |
|
|| |
|
≈ ε ~ t . |
(5.2.2) |
|
|||||
|
v |
|
|
||
Таким образом, отношение этого времени к классическому составляет величину порядка, то есть
νef |
≈ |
νjk |
. |
(5.2.3) |
|
||||
|
|
ε |
|
|
Кроме того, число запертых частиц в 
 ε раз меньше, чем пол-
ε раз меньше, чем пол-
ное число частиц. Таким образом, поток частиц поперек магнитного поля, определяется выражением
Γ ≈ − dn |
(∆rj )2 |
|
|
|
= −Def |
dn |
, |
(5.2.4) |
|||
|
ενef |
||||||||||
dr |
|
|
|
|
|
|
q2 |
|
dr |
|
|
Здесь D |
= ρ2 |
ν |
|
= D |
|
, |
D |
|
– классический коэффициент |
||
|
|
|
|
||||||||
ef |
j |
|
jk |
|
cl ε3/2 |
|
cl |
|
|||
диффузии.
Эта формула справедлива, если частица между столкновениями успевает совершить один или несколько полных оборотов по банановой траектории, прежде чем перейдет из запертых в пролётные, то есть
ν |
ef |
< ω |
≈ vT |
ε |
|
bounce |
R0q |
||
|
|
|
||
или
|
v |
ε3/2 |
|
|
|
νjk < |
Tj |
|
. |
(5.2.5) |
|
R0q |
|||||
|
|
|
|||
78
C ростом частоты столкновений плазма токамака переходит в «режим плато».
Режим плато
Этот режим реализуется при промежуточных частотах столкновений,
V ε3/2 |
< νjk < |
V |
|
|
T |
T |
. |
(5.2.6) |
|
|
||||
R0q |
|
R0q |
|
|
В этой области время между столкновениями уже меньше времени, за которое запертая частица обходит банан, но больше, чем время, за которое пролётная частица обходит тор по тороидальному направлению.
Для нахождения коэффициента диффузии в этой области воспользуемся стационарным кинетическим уравнением в τ -приближении.
|
∂f |
|
∂f |
= −νef ( f − f0 ). |
|
r |
∂r |
+ V |
∂V |
(5.2.7) |
Скорость можно представить как сумму продольной скорости и поперечной дрейфовой скорости:
r =V||h + VDr . |
(5.2.8) |
Дрейфовую скорость можно считать много меньше параллельной, VDr <<V|| .
Функцию распределения можно представить как сумму цилиндрически симметричной части и малой добавки, зависящей от полоидального угла.
f = f0 (r )+ f1 (r,θ). |
|
(5.2.9) |
||
В |
нулевом |
приближении |
имеем |
V|| = const; VDr = 0 , |
VDr ,∂∂fr0 = 0.
В первом приближении
V |
h, |
∂f1 |
|
+ |
V |
, ∂f0 |
|
= −ν |
ef |
f . |
(5.2.10) |
|
|| |
∂r |
|
|
|
D |
∂r |
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
79

Напомним, что магнитное поле в токамаке с круглыми магнитными поверхностями не имеет радиальной компоненты и не зави-
сит от тороидальной координаты, H ={0,Hθ,Hζ}.
Первый член в уравнении (5.2.10) можно преобразовать так:
|
|
|
∂f |
|
|
v|| |
|
∂f |
|
H |
|
∂f |
|
V|| |
∂f |
|
V |
|
h, |
1 |
|
= |
|
h |
1 |
≈ v |
|
θ |
1 |
= |
|
1 . |
(5.2.11) |
|
|
|
|
|
||||||||||||
|| |
|
∂r |
|
r |
θ |
∂r |
|
rHζ ∂θ qR ∂r |
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
Рассмотрим второй член в уравнении (5.2.10). Основной дрейф определяется градиентом поля
VD = ρ2VH [h, H ].
Направлен этот дрейф вдоль оси симметрии тора. Радиальная компонента его скорости определяется выражением
V |
≈ |
v2 |
sinθ ≡V 0 sinθ. |
(5.2.12) |
|
2ωH R |
|||||
Dr |
|
D |
|
Подставим (5.2.11) и (5.2.12) в (5.2.10). В результате получаем
∂f1 |
|
+ νf |
= −Asinθ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.2.13) |
|||||
∂θ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
νef |
qR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь νˆ |
= |
; |
A = |
V |
2q |
|
df |
0 |
. Решение этого уравнения имеет |
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
V |
|
|
|
2ω |
H |
V |
|
dr |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|| |
|
|
|
|
|| |
|
|
|
|
|
|
|
|
|
||
вид |
|
|
|
|
|
|
|
|
|
|
|
|
νA |
|
|
|
|
|
A |
|
|
|
f = C sinθ+C |
|
cosθ; |
C = − |
|
|
; C |
|
= |
|
. |
(5.2.14) |
|||||||||||
|
1+ ν2 |
|
1+ ν2 |
|||||||||||||||||||
1 |
1 |
|
|
|
2 |
|
|
|
1 |
|
|
|
2 |
|
|
|
||||||
Теперь нетрудно вычислить радиальный поток частиц:
Γ =  nVDr
nVDr  = ∫Rrdζdθ∫d3v 4VπDr2R ( f0 + f1 )=
= ∫Rrdζdθ∫d3v 4VπDr2R ( f0 + f1 )=
= ∫(1−εcosθ)sinθVD0 f1 |
dθ d3v. |
(5.2.15) |
|
2π |
|
При интегрировании по θ обратился в ноль. Обращаются также
вноль члены, пропорциональные sincosθ, sinθ2 cosθ , sinθcos2 θ .
Врезультате получаем
80
