Морозов Введение в теорию горячей плазмы Част2 2013

а функционал, отнесённый к единице длины системы, принимает вид

Пусть в цилиндре с отождествлёнными концами на одном периоде укладывается n периодов возмущения. Тогда kz = −n / R , и

В результате получаем функционал в следующем виде:

51

Здесь

Учитывая (3.5.2), функцию g можно переписать так:

52

Оценим теперь вклад в W последнего (интегрального) члена. Пусть m =1. Тогда обе функции f и g имеют порядок (kz r )2 , и

последним членом в (3.5.14) можно пренебречь. В этом случае величина W становится отрицательной, если

и любое начальное возмущение нарастает. Скорость нарастания возмущения можно оценить, используя уравнение (2.2.3). В фурье-

Здесь ρ0 = 2a∫2ρξ02ξ(2ardr) .

r

Максимальную величину инкремента по порядку величины можно оценить так:

Легко видеть, что этот инкремент по порядку величины равен отношению альфвеновской скорости к радиусу плазмы и может составлять в токамаке по порядку величины 10-8 с, то есть развитие такой неустойчивости является одним из наиболее быстрых процессов.

Пусть теперь m ≠1. Тогда функция g может быть порядка единицы в некоторой области значений nq(a) :

53

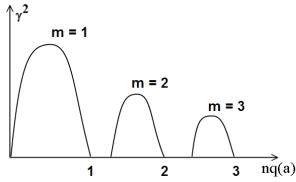
Зависимость γ2 от nq(a) качественно представлена на рис. 10.

Рис. 10. Качественная зависимость квадрата инкремента от nq(a) для различных мод

Как видно, области неустойчивости чередуются с областями устойчивости, где γ2 < 0. Именно в этих областях и работает токамак.

3.6. Ионная температурно-дрейфовая неустойчивость.

ITG-mode

В целом ряде экспериментов на токамаках оказывается, что зависимости от малого радиуса температуры и плотности оказываются подобными, то есть температура пропорциональна некоторой степени плотности. Возможно, что это явление связано с темпера- турно-дрейфовой неустойчивостью.

Эту неустойчивость следует рассматривать в двухжидкостной модели. Будем считать, что характерная частота неустойчивости

много меньше электронной ленгмюровской частоты, ω<< ωpe . В

этом случае можно пренебречь инерцией электронов. Будем предполагать также, что продольная теплопроводность достаточно вы-

54

сока, и как ионная, так и электронная температуры вдоль силовой линии не меняются, ||Ti,e = 0. В этом приближении уравнение им-

При рассмотрении ионов будем полагать, что поперечная длина волны много больше ионного ларморовского радиуса, k ρi <<1.

Кроме того, положим ω >> k\\vTi . Это позволяет пользоваться

МГД-уравнениями, то есть затуханием Ландау можно пренебречь. Уравнение непрерывности в фурье-представлении дает

Параллельная составляющая уравнения импульса имеет вид:

Вместо уравнения энергии, пренебрегая теплообменом, воспользуемся уравнением адиабаты. При этом показатель адиабаты положим равным 5/3:

Будем считать, что скорость ионов определяется дрейфом в электрическом поле.

Линеаризуем уравнение (3.6.6). Все величины в первой скобке – первого порядка малости. Поэтому произведение во второй скобке

можно вычислить в нулевом приближении: P0i n0 =T0i n0−2/3 . В нулевом приближении все величины зависят только от радиуса, поэто-

55

возмущения, вытянутые вдоль силовых линий. Поэтому будем считать, что kz << kθ . Имея в виду, что H0z >> H0θ , окончательно по-

лучаем

Система уравнений (3.6.2)–(3.6.4) и (3.6.10) имеет решение в том и только в том случае, если её определитель обращается в ноль, то есть

56

Это означает, что температура от периферии к центру не должна нарастать слишком быстро по сравнению с плотностью.

В реальном токамаке вследствие ненулевого шира при удалении от рациональной поверхности нарастает величина k||VTi и становит-

ся порядка ω. В этом случае необходимо кинетическое рассмотрение. Оно даёт следующее условие устойчивости:

Здесь zi = (k ρi )2 , I0 и I1 – модифицированные функции Бесселя.

В случае длинноволновых (в перпендикулярном магнитному полю направлении) волн, то есть для zi <<1 это условие упрощает-

ся:

в обратном случае. Этот факт был сначала обнаружен экспериментально на установке TFTR, на которой в результате нейтральной инжекции ионная температура впервые превзошла электронную. При этом формально критерий устойчивости, полученный ранее для Ti =Te , был нарушен, а неустойчивость не наблюдалась. И

лишь позднее этот эффект был объяснен теоретически О.П. Погуце

cсотрудниками.

3.7.Неустойчивость на запертых частицах

До сих пор мы изучали неустойчивости, которые с той или иной степенью точности можно исследовать в пределе цилиндра с отождествленными концами. Однако только в торе развивается целый ряд неустойчивостей, которые играют большую роль в аномальных переносах тепла и частиц. Таковы, например, баллонные моды (см.,

57

например, [4]). Рассмотрим одну из таких неустойчивостей – бесстолкновительную неустойчивость на запертых частицах.

В токамаке запертые частицы совершают периодические движения между точками отражения аналогично частицам в пробкотроне. Поэтому можно ожидать развития аналогичной неустойчивости. Но запертые частицы в токамаке погружены в море пролётных частиц, которые частично компенсируют разделение зарядов, создаваемое запертыми. Поэтому условие устойчивости будет несколько иным.

Очевидно, что для решения задачи должно быть использовано кинетическое уравнение. В нулевом приближении оно имеет вид

Для простоты положим E0 = 0. Более того, если возмущение

сильно локализовано по радиусу, можно перейти в систему отсчёта, в которой E0 = 0. Пусть функция распределения f мало отли-

чается от максвелловской с локальным значением температуры. Тогда можно написать

Будем рассматривать неустойчивость в пределе сильного магнитного поля, H → 0, когда можно пренебречь членом (V, f1 ). Тогда уравнение (3.7.3) перепишем так:

Это равенство справедливо при любых (нерелятивистских) скоростях, поэтому справедливо равенство

58

В дальнейшем для краткости будем опускать индекс j, означа-

ющий сорт частицы. Выразим производную ∂f1 из этого уравне-

∂V

ния и проинтегрируем по скоростям. В результате получаем поправку к f0 , связанную с тороидальностью:

Теперь вычислим поправку к функции распределения, связанную с возмущением электрического поля. Соответствующее кинетическое уравнение в линейном приближении имеет вид

Здесь тильдой обозначена поправка к функции распределения, связанная с возмущением электрического поля ϕ. Мы считаем

возмущения чисто потенциальными, H = 0. Левая часть этого уравнения – это полная производная по времени

то есть можно написать

и проинтегрировать полученное уравнение по времени от −∞ до t

Возмущение плотности находим, интегрируя f по скоростям.

Теперь для получения дисперсионного уравнения достаточно приравнять возмущения плотностей электронов и ионов. Учтём, что

(V, φ)= ddtϕ − ∂ϕ∂t .

Кроме того,

∂∂Vf = ∂∂Vf0 + ∂∂Vf1 = − mTV f0 + zeHmc [h, f0 ].

59

Возмущенный потенциал периодичен по азимутальному и тороидальному углам. Поэтому будем искать его в виде

Прямой фурье-анализ здесь затруднён, так как магнитное поле само зависит от полоидального угла.

Положим k ρi,e <<1 и пренебрежём отклонением частиц от ве-

дущего центра. Тогда в системе координат, в которой силовые линии прямые, получим возмущенную плотность.

лой тороидальности уравнение (3.7.11) упрощается. Кроме того, полагая k >>1, членом, пропорциональным ∂ϕ∂θ , можно пренебречь

по сравнению с членом, пропорциональным kϕ. В результате, приравнивая ne и ni , получаем

2nϕ = −∑ ∫0 exp(−iωt′+ik(θ′−θ)−il(ζ′−ζ))×

j −∞

Здесь мы положили Ti =Te . При интегрировании по скоростям

нужно отдельно проинтегрировать пролётные и запертые частицы. Для пролётных частиц

60