
Морозов Введение в теорию горячей плазмы Част2 2013
.pdfρ0 |
|
∂ |
2 |
ξ = ( P0,ξ)+ (γP0 ( ,ξ))+ |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
∂t |
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
[ |
|
|
] |
|
|
[ |
|
|
] |
|
0 |
|
||
|
|
1 |
0 |
|
|
0 |
1 |
|
0 |
H |
|
|||||||||
+ |
4π |
rotH |
,rot |
|
ξ, H |
|
+ |
4π |
rot |
rot |
ξ, H |
|
|
. |
(2.1.31) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Уравнение (2.1.31) должно быть дополнено граничными условиями.
Рассмотрим два варианта: на границе плазмы с идеально проводящей стенкой и на границе с вакуумом.
На границе со стенкой смещение плазмы в направлении, пер-
пендикулярном стенке, равно нулю: |
|
(ξ,n) = 0. |
(2.1.32) |
Здесь n – единичный вектор, нормальный к поверхности.
В идеально проводящей плазме составляющая электрического
поля, параллельная границе, обращается в ноль: |
|
|
|||||
[E,n]= 0. |
|
(2.1.33) |
|||||
C помощью уравнения (2.1.13) и соотношения V = V = |
d |
ξ ≈ ξ в |
|||||
|
|||||||
линейном приближении получаем |
dt |
||||||
|
|
||||||
|
|
∂ |
|
|
|
|
|
n, |
|
ξ,H0 |
= 0. |
(2.1.34) |
|||
∂t |
|||||||
|
|
|
|
|
|
||
Проинтегрировав (2.1.34) по времени, окончательно получаем граничное условие на бесконечно проводящей неподвижной стенке:
[n,[ξ,H]]= 0 . |
(2.1.35) |
На неподвижной границе «плазма–вакуум» магнитное поле перпендикулярно границе (в противном случае плазма будет вытекать
через границу вдоль поля): |
|
(H,n) = 0. |
(2.1.36) |
Величины в вакууме и в плазме будем обозначать соответственно индексами «e» (external) и «i» (internal). Равенство полных дав-
лений |
P + |
H 2 |
по обе стороны границы раздела имеет вид |
|
||||
8π |
|
|||||||
|
|
|
|
|
|
|||
P0i |
+ P1i |
+ |
1 |
(H0i + H1i )2 = |
1 |
(H0e + H1e )2 . |
(2.1.37) |
|
8π |
8π |
|||||||
|
|
|
|
|
|
|||
21

Все величины надо вычислять на смещённой границе r = r0 +(ξ,n0 ) , где индексом «0» обозначены радиус-вектор невоз-
мущенной границы и нормаль к ней. Разлагая в ряд по ξ, с учётом (2.1.30), получаем в первом приближении
−γPi0( ,ξ)+ 41π(H0i ,H1i ) = 41π(H0e ,H1e )+ (ξ8,nπ0) ∂∂n (H02e − H02i ). (2.1.38)
Вэтом уравнении все значения берутся на невозмущённой границе «плазма–вакуум».
Вплазме в системе отсчёта, движущейся вместе с граничной
поверхностью, электрическое поле E* = E + 1c [V,H0 ] обращается в
ноль. Тангенциальная её составляющая E*t |
непрерывна. Поэтому |
|||||||
E |
t |
+ |
1[V ,H |
] |
t |
=0. |
(2.1.39) |
|
|
|
c |
0 |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
Так как оба слагаемых в левой части формулы первого порядка
малости, их можно взять на невозмущённой границе: |
|
|||||
[E |
|
,n]= |
1V H |
|
. |
(2.1.40) |
|
e |
|
c n |
0e |
|
|
В вакууме электрическое поле выражается через векторный по-
тенциал, E = − |
∂A |
. Выражение (2.1.40) можно переписать в виде |
|||||
|
|||||||
|
|
]=[n0 |
∂t |
|
|
||
[n, |
∂A |
[∂ξ |
,H0e ]]. |
(2.1.41) |
|||
|
∂t |
c |
∂t |
|
|
||
Интегрируя это равенство по времени и учитывая, что магнит-
ное поле параллельно магнитной поверхности, получаем |
|
[n0 ,A]= −H0eξn . |
(2.1.42) |
На границе вакуум-стенка смещение обращается в ноль, поэтому [A,n]= 0.
2.2. Энергетический принцип
Уравнение (2.1.31) можно записать следующим образом:
|
∂2 |
ˆ |
|
ρ0 |
∂t2 |
ξ = Kξ . |
(2.2.1) |
22
Здесь Kˆ – дифференциальный оператор. Можно показать, что
если |
оператор |
ˆ |
– |
самосопряженный, |
то |
есть |
K |
∫dV (η, Kˆξ)= ∫dV (ξ, Kˆη), то можно написать функционал Φ, ва-
риация которого дает исходное уравнение.
В фурье-представлении двукратное дифференцирование по времени заменяется на умножение на квадрат частоты ω. Если мнимая часть частоты оказывается больше нуля, то система неустойчива. Анализ устойчивости может быть существенно упрощён. Для такого уравнения можно построить вариационный принцип. Подставляя в этот принцип вместо точного решения уравнения приближённую пробную функцию, качественно описывающую характер решения, можно с хорошей точностью получить собственные значения ω, то есть исследовать устойчивость системы.
Домножим уравнение (2.2.1) на ξ скалярно и проинтегрируем
по объёму и по времени по частям от −∞ до t и по пространству, полагая ξ(−∞) = 0.
|
3 |
t |
|
|
∂ξ |
2 |
+(ξ,Kˆ |
|
|
|
∫d |
|
|
|
|
= 0. |
(2.2.2) |
||||
|
r ∫ dt ρ0 |
|
|
|
ξ) |
|||||
|
|
−∞ |
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это равенство справедливо при произвольном t. Поэтому можно считать, что
1 |
|
|
∂ξ |
2 |
+(ξ,Kˆ |
|
3 |
|
|
|
|
|
r = 0. |
(2.2.3) |
|||||
2 |
∫ ρ0 |
|
|
|
ξ) d |
|
|||
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первый член в этом выражении можно интерпретировать как
кинетическую энергию системы |
T = |
1 |
∫ |
|
∂ξ 2 |
3 |
r , а второй, |
|
2 |
ρ0 |
|
d |
|
||||
|
|
|
∂t |
|
|
|
||
W = 12 ∫(ξ,Kˆξ)d3r , – как потенциальную.
Если W > 0 при всех возможных смещениях от положения равновесия, то система устойчива. В случае уравнения (2.1.31) потенциальная энергия имеет вид
23
W = − 12∫d3r(ξ,{ ( P0,ξ)+ (γP0 ( ,ξ))+
+ |
1 |
rotH |
|
,rot[ξ,H |
|
] |
+ |
1 |
rot rot[ξ,H |
|
],H |
|
. |
(2.2.4) |
|
|
|
|
|
||||||||||
|
4π |
0 |
|
0 |
|
|
4π |
0 |
|
0 }) |
|
|
||
Преобразуем первый интеграл в фигурных скобках. Интегрирование ведется по объёму, занятому плазмой, так как вне его давление равно нулю. Обозначим
f ≡ (ξ, P0 )+ γP0 divξ. |
(2.2.5) |
Интегрируя по частям, находим |
|
∫d3r(ξ, f )= ∫(dS,ξ) f − ∫d3r f divξ . |
(2.2.6) |
В первом члене интегрирование ведётся по поверхности, ограничивающей плазму. Рассмотрим теперь последний член в интеграле (2.2.4). Обозначим
Q = rot[ξ,H0 ]. |
|
|
|
(2.2.7) |
||||||||
Последний член в (2.2.4) преобразуется как |
|
|||||||||||
|
1 |
|
∫d3r(ξ,[rot Q,H0 ])= − |
1 |
|
∫d3r(rotQ,[ξ,H0 ])= |
|
|||||
|
4π |
|
|
|||||||||
|
|
1 |
|
|
|
4π |
|
|||||
= − |
|
|
∫d3r{div[Q,[ξ,H0 ]]+Q2}= |
|
||||||||
|
|
|
|
|||||||||
|
|
|
|
|
4π |
|
|
|
|
|||
= − |
1 |
∫(dS,[Q,[ξ,H0 ]])− |
1 |
∫d3r(rot[ξ,H0 ])2 . |
(2.2.8) |
|||||||
4π |
4π |
|||||||||||
В первом интеграле интегрирование снова ведется по границе плазмы. Раскрывая двойное векторное произведение и учитывая, что поверхность плазмы параллельна магнитному полю, получаем выражение для потенциальной энергии
W = |
1 |
∫d3r γP0 (divξ)2 + |
1 |
(rot[ξ,H0 ])2 + |
(ξ, P0 )divξ− |
|
|||||||
2 |
|
|
|||||||||||
|
|
|
|
4π |
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
([ξ,rotH0]],rot[ξ,H0 |
]) |
− |
|
|
|
|
|
||||
4π |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
−1 |
|
(dS,ξ) |
(ξ, P )+γP divξ− |
1 |
(Q,H |
|
) . |
(2.2.9) |
|||||
|
|
0 |
|||||||||||
|
2∫ |
|
|
0 |
0 |
|
|
4π |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
24
Поверхностный интеграл
S =1 |
|
(dS,ξ) ξ, P )+γP divξ− |
1 |
(Q,H |
|
) |
||||||||||||
|
|
0 |
||||||||||||||||
|
|
2 ∫ |
|
0 |
|
|
|
0 |
|
|
|
4π |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
преобразуем с помощью равенства (3.1.38): |
||||||||||||||||||
|
|
1 |
∫ |
|
|
|
|
1 |
|
H02i − |
∂H 2 |
|
|
|
|
|||
S |
= |
|
|
ξ, P0 + |
|
|
|
|
|
|
|
+ |
|
|
||||
2 |
|
(dS,ξ) |
8π |
|
0e |
|
|
|||||||||||
|
|
|
|
|
|
|
|
∂n |
|
|
|
|
||||||
|
(H0i ,H1i )−(H0e ,H1e ) |
|
|
1 |
|
|
|
|
|
|
|
|
||||||
+ |
|
|
|
|
|
|
− |
|
|
(Q,H0 ) . |
|
|
|
(2.2.10) |
||||
|
|
|
4π |
|
|
4π |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Величину Q надо вычислять на подходе к границе плазмы со
стороны плазмы. Эту величину можно определить, подставляя уравнение (2.1.13) в (2.1.16) и интегрируя последнее по времени:
Q=rot[ξ,H0]=Hi1 . |
(2.2.11) |
Скалярное произведение (dS,ξ)можно выразить через модуль
элемента поверхности и нормальную к поверхности составляющую смещения, dSξn . Тогда
|
|
|
1 |
∫ |
|
|
|
∂ |
H 2 −H 2 |
|
|
(H ,H ) |
|
|||||||
|
|
|
|
|
|
|
ξn2 |
|
|
|
|
|
|
|
|
|
0e 1e |
|
|
|
S |
= |
|
|
|
dS |
|
P0 + 0i |
|
0e |
−ξn |
|
|
. |
(2.2.12) |
||||||
|
|
|
2 |
|
|
|
|
∂n |
|
|
8π |
|
|
|
|
4π |
|
|
||
Последний член можно преобразовать так: |
|
|
||||||||||||||||||
S1 ≡ |
1 |
∫(dS,ξ)(H0e ,H1e )= |
|
|
|
|
|
|
||||||||||||
4π |
|
|
|
|
|
|
||||||||||||||
= |
|
1 |
|
∫ |
dS |
[H |
,[ξ,H |
|
]] |
+H |
|
(H |
,ξ) . |
|
(2.2.13) |
|||||
|
4π |
|
|
|
||||||||||||||||
|
|
{ |
1e |
|
0e |
|
|
0e |
1e |
|
} |
|
|
|
||||||
Последний член обращается в ноль, так как магнитное поле на границе плазмы перпендикулярно поверхности плазмы. Снова перейдем к интегрированию по объёму, но теперь будем вести интегрирование по вакуумной области. При этом знак нормали к поверхности плазмы имеет другой знак:
S =− |
1 |
|
d3rdiv H |
|
,[ξ,H |
] . |
(2.2.14) |
4πV∫ |
|
||||||
1 |
[ |
1e |
|
0e ] |
|
||
|
|
e |
|
|
|
|
|
25
Учитывая, что в вакууме rotH =4cπj=0, раскроем двойное векторное произведение и подставим H1 =rotA1 . При этом получаем
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
∂ |
|
2 |
2 |
S |
=− |
|
∫d3r(rotA1)2 + |
1 ∫dSξn2 |
P0 |
+ H0i −H0e . |
|||||||||||
|
|
∂n |
|||||||||||||||
|
|
|
|
4πV |
|
|
2 |
|
|
|
|
8π |
|
||||
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
И окончательно |
|
|
|
|
|
|
|
|
|
|
|
||||||
W = |
1 |
∫d3r γP0 (divξ)2 |
+ |
1 |
(rot[ξ,H0 ])2 |
+(ξ, P0 )divξ− |
|||||||||||
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
4π |
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
([ξ,rotH0]],rot[ξ,H0 ]) |
+ |
|
|
|
|
|
||||||||
4π |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
∂ |
|
|
2 |
2 |
|
||
+ |
|
∫d3r(H1e )2 − |
1 ∫dSξn2 |
P0 |
+H0i −H0i . |
|
|||||||||||
|
|
∂n |
|
||||||||||||||
|
8πV |
|
|
|
2 s |
|
|
|
|
|
8π |
|
|
||||
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.2.15)
(2.2.16)
Пользоваться энергетическим признаком удобно в тех случаях, когда нужно получить общие сведения об устойчивости плазменной конфигурации. Он, в частности, позволяет приближенно быстро найти область неустойчивости, что при нахождении её методом малых колебаний требует значительного времени.
ГЛАВА 3. УСТОЙЧИВОСТЬ ИДЕАЛЬНОЙ ПЛАЗМЫ В СИСТЕМАХ С ЗАМКНУТЫМИ МАГНИТНЫМИ ПОВЕРХНОСТЯМИ
В этой главе мы рассмотрим конкретные неустойчивости, характерные для плазменных конфигураций в термоядерных установках.
3.1. Желобковая неустойчивость
Одной из наиболее опасных оказывается так называемая желобковая (flute-like в зарубежной литературе) неустойчивость. Её ещё называют перестановочной или конвективной неустойчивостью. Эта неустойчивость весьма опасна, так как практически не возмущает магнитного поля.
Рассмотрим эту неустойчивость в пробкотроне.
26
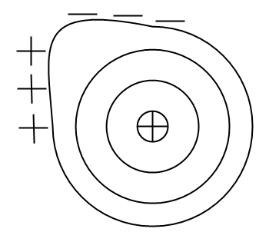
Рис. 4. Желобковое возмущение
Пусть трубка плазмы, вытянутая вдоль силовых линий, всплывает из более горячей и плотной области в менее плотную и более холодную. Сечение магнитных поверностей пробкотрона, перпендикулярное оси, показано на рис. 4. Это приводит к изгибанию линий постоянной плотности. Пусть магнитное поле направлено за плоскость чертежа. Если сечение проходит через середину пробкотрона, в этом сечении магнитное поле спадает к периферии. При этом положительно заряженные частицы дрейфуют в направлении
вектора [H, H], то есть против часовой стрелки, а отрицательно
заряженные – в противоположном направлении. В той области, где трубка «всплыла», на её краях выступят нескомпенсированные заряды и возникнет электрическое поле в полоидальном направлении. Под действием этого поля как положительно, так и отрицательно заряженные частицы будут испытывать ExВ-дрейф, приводящий к дальнейшему «всплыванию» частиц. Но частицы движутся также и вдоль силовых линий от пробки к пробке, попадая в те области вблизи пробок, где магнитное поле возрастает к периферии. В этих областях они будут дрейфовать к оси пробкотрона. В пробкотроне частицы плохо проникают в область пробок. В результате частицы в среднем будут смещаться наружу, то есть плазма будет неустойчива.
27
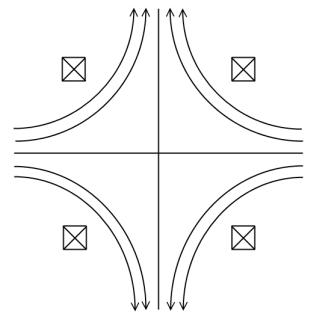
Рис. 5. Антипробкотрон
В антипробкотроне (рис. 5), когда поля от двух кольцевых токов направлены навстречу друг другу, магнитное поле всюду будет спадать по радиусу, и плазма будет устойчива. Но в экваториальном сечении в магнитном поле будет существовать круговая щель, через которую частицы будут быстро уходить из ловушки вдоль поля. Такая система для удержания плазмы непригодна.
Мы качественно рассмотрели желобковую неустойчивостью. Перейдем теперь к её количественному описанию.
Пусть силовая трубка, вытянутая вдоль силовых линий, «всплыла» из положения 1а–1б в положение 2а–2б (рис. 6), причём время «всплытия» много больше, чем время пролёта частиц между пробками.
28

Рис. 6. Всплытие трубки в пробкотроне
Тогда при «всплытии» сохраняется продольный адиабатический
инвариант J =m |
∫ |
v||dl . Выражая параллельную составляющую им- |
||||||||
|
||||||||||
пульса |
через |
магнитный момент |
µ=mv2 |
и полный импульс |
||||||
|
|
|
|
|
|
|
|
|
2H |
|
p = p2 + p2 , |
получаем следующее выражение для адиабатическо- |
|||||||||
|| |
|
|
|
|
|
|
|
|
||
го инварианта: |
|
|
|
|
|
|||||
J = ∫ |
|
|
|
|
|
|||||
|
p2 −2mµH . |
|
(3.1.1) |
|||||||
Интегрирование здесь ведется между точками отражения. При смещении трубки из положения 1 в положение 2 меняются магнитное поле и точки отражения. При этом адиабатический инвариант не меняется:
δJ = ∫δdl |
|
|
|
|
|
|
|
|
|
|
∫δ(p2 )−2mµδH |
|
dl=0 . |
(3.1.2) |
|||||||||||
|
p |
2 |
−2mµH + |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 p |
2 |
−2mµH |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Найдем среднее за период |
τ= ∫dt= ∫dlv |
|
изменение энергии ча- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|| |
|
|
|
|
стицы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
__ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
p |
dl |
|
|
|
|
|
|
|
δH dl−m |
|
|
|
|
|
|||||||||
δε=δ1 |
|
|
= |
|
1 |
|
µ |
|
|
v |
δdl |
, |
(3.1.3) |
||||||||||||
τ |
∫2m v |
|
|
dl |
|
∫ |
|
v |
|
|
∫ |
|| |
|
|
|
|
|||||||||
|
|
|
|
|
|
|| |
|
|
∫ v |
|
|
|| |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|||

а также вариацию магнитного поля δH . В установках типа токамак или стелларатор параметр β=8HπP2 , равный отношению плазменно-
го давления к магнитному, мал, и возмущение магнитного поля можно считать практически вакуумным, то есть для него можно положить rotH = 0. Вычислим циркуляцию вектора Н по замкнутому контуру 1а–1б–2б–2а–1а, показанному на рис. 6. Будем считать контур узким, то есть интегралами на участках 1б–2б и 2а–1а можно пренебречь. Длина участка 1а–1б равна dl, магнитное поле на этом участке равно H. Длина участка 2а–2б равна dl+δdl, а ма г- нитное поле, соответственно, равно H +δH . Таким образом, из условия обращения в ноль циркуляции магнитного поля получаем
δdl+dl |
δH |
=0. |
(3.1.4) |
|
H |
||||
|
|
|
Если потенциальная энергия при отклонении от равновесия растёт, то система устойчива. Потенциальная энергия плазмы в трубке – это сумма энергий всех частиц в этой трубке. Вероятность пребывания частицы на отрезке силовой линии dl равна отношению времени пребывания на этом отрезке к времени пребывания между пробками
Подставляя (3.1.4) в (3.1.3) и учитывая, что µ=mv2 , получаем
2H
δε= |
1 |
∫ |
mv2 |
2 |
|
δH dl |
|
|
|
|
2 |
+mv|| |
|
H v . |
(3.1.5) |
||
dl |
||||||||
|
∫v |
|
|
|
|
|| |
|
|
|
|| |
|
|
|
|
|
|
|
Вероятность пребывания частицы на отрезке dl равна отношению времени пребывания на нём к п ериоду обращения между пробками:
dW(ε,µ,l)= |
dt |
= |
dl/v|| |
. |
(3.1.6) |
|
dl |
|
|||||
|
|
∫ |
dl/v |
|
||
|
∫v |
|
|| |
|
|
|
|
|
|
|
|
|
|
||
Пусть в интервале dεdµ на данной силовой линии содержится
dεdµF(ε,µ) частиц. Тогда полное приращение энергии в трубке сечением dS имеет вид
30
