Морозов Введение в теорию горячей плазмы Ч.1 2011

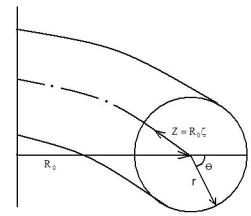
удобно ввести квазицилиндрическую систему координат r, , (см. рис. 14). Углы и называют полоидальным и тороидальным углами соответственно. Тороидальный угол в представлении цилиндра с отождествлёнными концами связан с координатой z следующим образом:

Область его определения можно распространить от − до при условии, что все физические величины периодичны по с периодом 2 . С учетом (II.2.9) уравнение силовых линий можно переписать в виде

Рис. 14. Квазицилиндрическая система координат.

61

Если силовая линия, совершив целое число n

оборотов по тороидальному углу, сделает целое число оборотов m по полоидальному углу, то силовая линия замкнется сама на себя. Математически это выражается так:

n − 0 2 n, m − 0 2 m. Из (II.2.10) видно,

что это условие может выполняться не на всех магнитных поверхностях, а лишь на тех, для которых q mn , т.е. является рациональным числом. Такие поверхности, называются рациональными. Они распределены по радиусу всюду плотно, так же, как рациональные числа распределены по числовой оси.

Большую роль в теории устойчивости плазмы играет перекрещенность силовых линий. Перекрещенность появляется, если шаг винтовых линий (II.1.26) меняется с радиусом. В случае, если q от радиуса не зависит, перекрещенности нет. Количественной характеристикой перекрещенности является безразмерный параметр, называемый широм S ( в переводе с английского - ножницы):

Штрих здесь означает производную по радиусу.

В горячей плазме многие физические величины точно или приближенно постоянны на магнитной поверхности. Поэтому бывает удобно

62

ввести систему координат, одной из переменных в которой является величина, маркирую щая магнитную поверхность. При цилиндрической симметрии таким параметром является просто радиус. В случае нарушения такой симметрии маркировать магнитную поверхность могут тороидальный или полоидальный магнитные потоки.

Здесь интегрирование ведется по поверхности,

ограниченной данной магнитной поверхностью. В случае тороидальной симметрии (II.2.12) можно представить так:

где интегрирование по r ведется от нуля до r ,

соответствующего данной магнитной поверхности. Полоидальный поток в случае тороидальной симметрии и малой тороидальности может быть

представлен в виде:

63

произвольном сonst.

направлении.

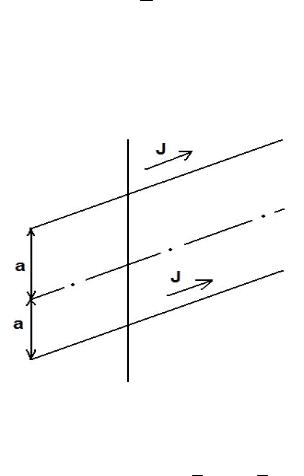
Выше мы рассмотрели модель токамака в виде цилиндра с круговыми сечениями магнитных поверхностей. Приблизительно таковыми они и были в первых токамаках с лимитером, ограничивающим плазменный шнур. В большинстве современных токамаков используется так называемая диверторная конфигурация. Для создания такой конфигурации параллельно основному току разряда по специальному кольцу запускается ток дополнительный. Структура магнитных поверхностей в такой системе качественно описывается моделью Бузера, в которой полагается, что ток разряда сосредоточен на магнитной оси, а дополнительный ток равен ему по величине. Модель представлена на рис. 15. Два параллельных тока J текут в направлении оси z на расстоянии a от неё. Векторный потенциал такой системы токов даётся выражением:

64

где

Рис. 15. Конфигурация токов в модели Бузера.

Причем здесь размерные переменные x и y заменены безразмерными x → ax , y → ay . Токи создают полоидальное поле, на которое наложено однородное поле, направленное вдоль оси z. Величина пропорциональна магнитному потоку и маркирует магнитную поверхность. Вблизи проводников магнитные поверхности круговые.

65

Действительно, введём новую переменную x′ x − 1. Вблизи верхнего проводника на Рис. II.5 можно положить x′ 1, y 1. Разлагая (II.2.18)

вряд по x’ и y’, получаем:

≈ 4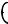 x′ 2 y2 ,

т.е. сечения поверхностей сonst являются кругами. Начало координат является называемой х-точкой. Действительно, при x→ 0 выражение (II.2.18) переходит в следующее:

x y.

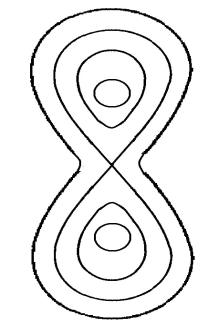
Cечение магнитных поверхностей в модели Бузера показано на рис. 16. Поверхность, для которой 1, отделяет области магнитных поверхностей, охватывающих одну ось, от области поверхностей, охватывающих обе оси. Она называется сепаратрисой.

Простое определение для q (II.1.21) здесь уже неприменимо. Поэтому выразим эту функцию через магнитные потоки. Формулу (II.1.21) можно

Такое определние q пригодно для любой формы

66

магнитных поверхностей. Заметим, что вблизи х-точки H → 0, поэтому при приближении к сепаратрисе q → .

Рис. 16.Сечения магнитных поверхностей в модели Бузера

67

II. 3. Устойчивость магнитных поверхностей

Описание магнитных полей токамака, приведённое в предыдущем разделе, справедливо лишь в первом приближении. На эти поля обычно наложены различные возмущения, связанные как с неидеальностью магнитных систем, так и с различными процессами в плазме. Поэтому встаёт вопрос об устойчивости магнитных поверхностей к внешним возмущениям.

Невозмущенное полоидальное поле в системе с круглыми магнитными поверхностями можно описать с помощью векторного потенциала со следующими компонентами:

Ar −H0r ,

A − Rr Hq0 dr.

Действительно, беря ротор от векторного потенциала, получаем:

68

H ≈ H0.

Возмущения тороидального поля учитывать не будем.

Уравнение для магнитных поверхностей имеет вид (II.2.15), H, 0, что можно переписать следующим образом:

Будем решать задачу с помощью теории возмущений, т.е. представим решение в нулевом приближении плюс малое возмущение и сохраним в уравнении только линейные по возмущениям члены.

69

Из (II.3.7) и (II.3.8) видно, что винтовое возмущение приводит не к разрушению магнитных поверхностей, а лишь к изгибанию их, если мы находимся не слишком близко к резонансной поверхности, где шаг винтового возмущения совпадает с шагом силовой линии, т.е. в ноль обращается знаменатель в выражении (II.3.8). В этом случае теория возмущений неприменима, и приходится пользоваться другим методом нахождения решения.

Введём новую переменную m − n и

вернемся к полному уравнению (II.3.4).

70