
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf
S |
e |
, |
r |
. |
4 p |
|
|||
|
|
S |
||
Величину S называют радиусом Штермера. Функцию Q теперь можно представить в безразмерном виде:
|
|
|
̂ |
|
|
|
Q |
sin |
|
2 |
. |
(I.3.4) |
|
sin |
||||||
|
2 |
|
|
|
||
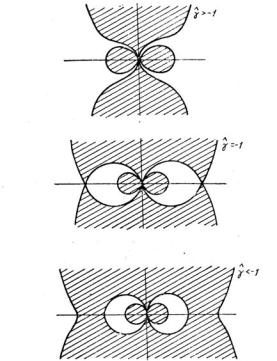
На рис. 5 представлены области |
Q 1 (эти |
|||||
области заштрихованы) и Q 1.
При −1 разрешенная зона распадается на две несвязанные между собой области. Края запрещенной области при этом смыкаются в экваториальной плоскости при 1. Частицы, находящиеся во внешней разрешенной области, не могут попасть во внутреннюю часть, так как при этом должны были бы пересечь запрещенную область. И обратно, частицы, находящиеся во внутренней разрешенной области, не могут покинуть ее и остаются захваченными. Это обстоятельство служит основой для объяснения существования радиационных поясов Земли и для конструирования так называемых дипольных ловушек для магнитного удержания плазмы.
Рассчитаем теперь поток частиц, который может приходить из бесконечности в данную точку пространства. Пусть на бесконечности имеется изотропный поток частиц с заданной кинетической энергией. Векторный потенциал на бесконечности обращается в ноль. Из выражений (I.1.10) и (I.3.3)
31
видно, что в этом потоке присутствуют частицы со
всевозможными значениями . Однако в точку с заданными r и могут попасть лишь те частицы,
для |
|
которых |
|
|Q| 1, |
т.е. |
||
2 |
|
|
2 |
|
|
|
|
sin − |
sin |
≤ 2 ≤.- sin − |
sin |
. Поток частиц в |
|||
|
|
|
|
||||
точке наблюдения, тем не менее, может быть изотропным, если на угол между единичным вектором в полоидальном направлении и вектором скорости частицы, т.е. на величину Q не наложено никаких дополнительных ограничений. Такие ограничения, однако, возникают в точках наблюдения, для которых 1.
В такую точку из бесконечности не могут
прийти те частицы, для которых −1. Таким образом, в таких точках величина Q, т.е. косинус угла между направлением скорости и единичным вектором в полоидальном направлении, ограничена неравенством
|
|
− |
|
2 |
|
|
sin |
≤ Q ≤ 1. |
(I.3.5) |
|
|
|
|
sin |
2 |
||||||
|
|
|
|
|
|
|
||||
Если − |
2 |
|
|
sin |
|
≥ 1, то в эту точку вообще не |
|
|||
sin |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
могут приходить частицы с заданной энергией. Эту энергию называют энергией отсечки.
Поток частиц в точке наблюдения определяется теоремой Лиувилля. Так как фазовая плотность частиц вдоль фазовых траекторий сохраняется, а кинетическая энергия частиц в постоянном магнитном поле постоянна, поток частиц вдоль траекторий в обычном пространстве должен сохраняться. Таким образом, полный поток
32
заряженных частиц в точке наблюдения при1 равен потоку на бесконечности, а при 1 - потоку в единицу телесного угла на бесконечности, умноженному на величину телесного угла, определяемого неравенством (I.3.5).
.Рис. 5. Разрешенные и запрещенные зоны в поле магнитного диполя
33

I.4. Приближенные методы расчета траекторий. Адиабатические инварианты. Дрейфовое приближение.
Как можно было видеть, точный расчет движения частиц даже в случае простейших конфигураций магнитного поля является довольно сложной задачей. Трудности многократно возрастают в случае реальных конфигураций поля. Поэтому были развиты и успешно работают приближенные методы для тех случаев, когда характерный размер, на котором существенно меняется поле, много больше ларморовского радиуса частицы, а характерное время изменения поля много меньше циклотронной частоты.
В однородном поле траектория частицы представляет собой спираль с радиусом mVeH c .
Введем цилиндрическую систему координат с осью z, совпадающей с осью спирали. Движение частицы будет периодическим по угловой координате . Пусть теперь магнитное поле стало слабо неоднородным или медленно меняющимся во времени в указанном выше смысле. Как известно из механики (см. напр. [4]), если частица совершает почти периодическое движение по обобщенной
координате q, то величина I Pdq, где
интегрирование ведется по невозмущенной траектории, сохраняется. В нашем случае должна
34

сохраняться величина |
I Pd , |
|
где P |
∂L |
||||||
|
|
|||||||||
mV |
e |
A . Вычислим эту величину. |
∂ |
|||||||
|
||||||||||
c |
|
|||||||||
P d |
const |
2 V |
e |
A d |
|
|||||
c |
|
|||||||||
|
|
|
mV2 c |
|
e |
|
|
|
||
|
|
|
2 eH |
|
|
c |
A dl. |
|
||
Элемент dl можно представить в виде dl d . Используя теорему Стокса, можно написать:
P d 2 |
mV2 c |
− |
e |
rotA dS |
(I.4.1) |
|
|
eH |
c |
||||
2 |
mV2 c |
HdS. |
|
|||
eH |
|
|||||
Здесь dS - элемент поверхности, перпендикулярной полю. Знак « минус» перед членом, содержащим ротор, связан с тем, что направление вращения частицы противоположно направлению обхода контура в теореме Стокса. Последний член в (I.4.1) приближенно равенHdS 2H. Подставляя это выражение в (I.4.1),
окончательно получаем:
P d |
2 |
c |
mV2 |
− |
ė |
mV2 c2 |
H |
|
(I.4.2) |
|
e |
c |
|||||||||
|
|
eH |
|
e2H2 |
|
|
|
cm mV2e H .
35

Таким образом, величина mV2H2 является
первым адиабатическим инвариантом. Она с точностью до постоянной совпадает с магнитным моментом, создаваемым частицей, вращающейся по ларморовской окружности. В большинстве задач по магнитному удержанию она сохраняется с хорошей степенью точности.
С помощью первого адиабатического инварианта можно проиллюстрировать запирание частицы в простейшей магнитной ловушке – пробкотроне. Она представляет собой два кольца с током, расположенные на общей оси (см. рис. 6). Пусть нерелятивистская частица начинает движение из точки 0 в направлении точки 1. Заметим, что H0 H1. Используя выражение для кинетической энергии Ekin m2 (v2 v2 ) const, и
связь между компонентой скорости, перпендикулярной магнитному полю, и , можно найти параллельную магнитному полю составляющую скорости:
|
V2 |
|
2Ekin |
− |
2 H |
|
0. |
|
|||||
|
|
m |
|
|
|||||||||
|
|
|
|
|
m |
|
|
|
|
|
|||
Так как кинетическая энергия сохраняется, |
|
||||||||||||
можно найти связь между параллельными |
|
||||||||||||
скоростями и магнитными полями в тт. 0 и 1: |
|
||||||||||||
V0 2 |
|
2 H0 |
V1 2 |
|
|
2 H1 |
, или |
|
|||||
|
m |
|
|
m |
|
|
|||||||
V1 2 |
|
|
V0 2 |
|
|
2 |
H0 − H1 . |
(I.4.3) |
|||||
|
|
m |
|||||||||||
Очевидно, что правая часть выражения (I.4.3) должна быть неотрицательна. Таким образом,
36

m V0 2
область, в которой H1-H0 2 , оказывается
недоступной для рассматриваемой частицы. Точка, в которой параллельная скорость обращается в ноль, является точкой поворота и определяется условием:
H1 − H0 |
m V0 2 |
|
2 . |
(I.4.4) |
Рис.6. Схема силовых линий в пробкотроне. Квадратиками обозначены кольца с током
Это условие можно переписать так:
|
H1 |
|
1 |
|
V0 |
2 |
|
||
|
|
|
. |
(I.4.5) |
|||||
|
H0 |
2 |
|
V0 |
|||||
|
|
|
|
|
|||||
Отношение |
V |
|
ctg |
является |
котангенсом |
||||
V |
|||||||||
37
угла между скоростью и магнитным полем в точке 0. Этот угол называется питч-углом. Если точка 1 соответствует максимальному значению магнитного поля в пробкотроне, то все частицы, для
|
|
|
|
|
H1 |
− 1 2 |
|
, |
|
которых 0, где |
0 |
arctg |
|
2 |
|
||||
H0 |
оказываются запертыми. Точка 1 в этом случае называется пробкой. Частицы, для которых 0, уходят из ловушки. Соответствующий телесный угол называется конусом потерь.
Очевидно, что запертые частицы совершают квазипериодическое движение между пробками (квазипериодическое, а не просто периодическое потому, что частица еще дрейфует вокруг оси ловушки, как мы увидим далее). Поэтому должен существовать второй адиабатический инвариант
m v |
e |
A dl |
const. |
(I.4.6) |
c |
Так как H rotA, можно положить A 0. Параллельную составляющую скорости можно выразить через полную скорость и первый адиабатический инвариант:
V |
V2 |
− V2 |
|
V 1 − |
|
2 H |
. |
|
(I.4.7) |
|||
|
Vm |
|
||||||||||
Тогда выражение (I.4.6) можно представить в |
||||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
I3 1 |
− H dl |
const. |
|
|
2 |
|
|
. (I.4.8) |
||||
|
mV |
2 |
|
Ekin |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
38

Здесь интеграл берется между двумя точками поворота.
Выражение (I.4.8) определяет второй адиабатический инвариант.
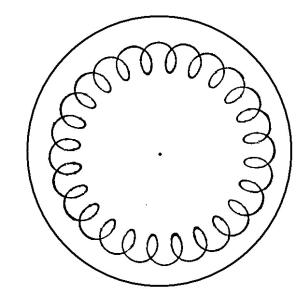
Как уже отмечалось, в пробкотроне частица не только колеблется между точками отражения, но и дрейфует вокруг оси системы. Действительно, в плоскости,проходящей через точку 0, магнитное поле нарастает к оси. Следовательно, ларморовский радиус на меньших расстояниях будет меньше. Следовательно, частицы будет дрейфовать в полоидальном направлении (см. рис. 7)
Таким образом, наблюдается третий вид квазипериодического движения, и должен существовать еще один, третий адиабатический инвариант,
I3 |
m V |
e |
A dl. |
(I.4.9) |
c |
При интегрировании вклад дает только средняя перпендикулярная скорость, которой можно пренебречь. В результате получаем:
I3 |
e |
AL d L |
e |
rotA dS |
(I.4.10) |
c |
c |
H dS .
s
Здесь – магнитный поток внутри траектории. Адиабатические инварианты, полученные на примере движения частицы в пробкотроне, имеют гораздо более общий смысл. При этом условия
39
сохранения второго и третьего инвариантов являются гораздо более строгими, чем первого. Действительно, если для первого инварианта магнитное поле должно меняться на расстояниях, значительно превышающих ларморовский радиус за времена, не превышающие обратную ларморовскую частоту, то во втором и третьем случаях такими параметрами являются расстояние между пробками и радиус усредненной траектории и соответствующие периоды квазипериодических движений, которые обычно значительно больше.
Рис. 7. Проекция траектории частицы в пробкотроне на плоскость, перпендикулярную оси установки.
40
