Морозов Введение в теорию горячей плазмы Ч.1 2011

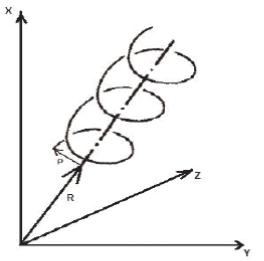
В слабо неоднородных и медленно переменных полях скорость частицы можно представить как быстрое вращение вокруг ведущего центра и медленное смещение центра вдоль поля плюс медленный дрейф поперек. Координату частицы можно представить как координату ведущего центра R плюс расстояние от него до частицы (рис. 8). Скорость v также можно представить как сумму скорости ведущего центра V и скорости быстрого вращения вокруг него u:

r R ; v V u; u .

Уравнение движения

m v F R, t ec v, H

можно разложить в ряд по /R. Здесь F – сила, действующая на частицу (за исключением силы Лоренца).

e/c u, H R e/c V, H R

e/c u, H R .

41

Усредним (I.4.11) по времени t, превышающему период быстрых осцилляций 1/ H, но меньшему характерного времени

изменения полей, 1/ H t .

Рис. 8. Траектория частицы в магнитном поле

Члены, содержащие нечетные степени быстро осциллирующих величин при усреднении зануляются. Усредненное уравнение имеет вид:

m V F R e/c V, H R e/c u, , H . (I.4.12)

Угловые скобки обозначают усреднение по времени. Вычтем из полного уравнения (I.4.11) усредненное уравнение (I.4.12)

42

m u e , E e/c u, H e/c V, , H (I.4.13)

e/c u, , H − e/c u, , H .

Внулевом по параметру /R порядке разложения имеем:

Как и ожидалось, в этом приближении уравнение для быстрых осцилляций совпадает c уравнением движения частицы в однородном поле. Можно написать:

e/c H, u, , H .

Раскрывая двойное векторное произведениеH, V, H H, V , H V H2 и подставляя его в (I.4.16), разрешаем последнее относительно V :

43

− H12 H, u, , H .

Первый член в правой части (I.4.17) описывает дрейф частицы под действием внешней силы F. Это может быть, например, электростатическая сила или сила гравитации. Обычно скорость такого дрейфа обозначается как VD. В случае дрейфа под действием электрического поля (такой дрейф в современной литературе называется ЕхВ-дрейфом) сила F равна eE, а скорость электрического дрейфа может быть представлена в виде

Заметим, что эта скорость не зависит ни от заряда, ни от массы частицы. Таким образом, как электроны, так и ионы всех сортов под действием поперечного к магнитному электрического поля дрейфуют в одном направлении с одинаковыми по величине скоростями.

Второй член в правой части уравнения (I.4.17) описывает инерционный дрейф и имеет порядок

силовой линии, направленный от центра кривизны к силовой линии, на которой находится частица.. Он

44

может быть выражен через градиент модуля

Кроме того, дополнительный вклад в инерционный дрейф появляется в случае

поляризационным. Он оказывается важным при изучении дрейфовых волн.

Легко видеть, что последний член в правой части уравнения (I.4.17) связан с неоднородностью магнитного поля. Соответствующий дрейф называют градиентным. Точная процедура усреднения довольно громоздка. Она аккуратно выполнена в обзоре [5]. Однако скорость градиентного дрейфа с точностью до множителя порядка единицы можно получить из простых

полем H , причем оба поля направлены вдоль оси z,

и H H (cм. рис. 9)

45

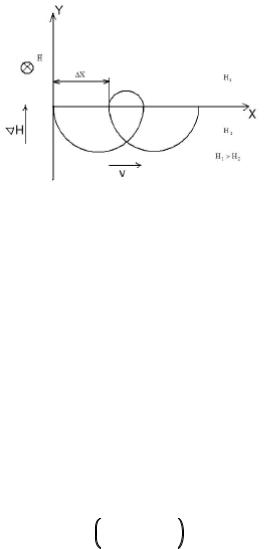
Рис. 9. Траектория частицы в ступенчатом поле

Пусть положительно заряженная частица стартует из начала координат вертикально вниз в отрицательном направлении вдоль оси y со скоростью u . Описав полуокружность радиуса

mu c / eH2 , она перейдет в верхнюю полуплоскость и опишет в ней полуокружность радиуса 1 mu c / eH1 . При этом она сместится от своего начального положения на расстояние

x 2 − . Будем считать, − / 1,

что эквивалентно H − H / H 1. Скорость дрейфа может быть вычислена как VH x / t , где время t 2 / H. Разность − можно представить в виде

Переходя от ступенчатой модели магнитного

46

поля к непрерывной, можно написать:

Подставим (I.4.20) и (I.4.21) в выражение для скорости и получим модуль скорости дрейфа:

Для того, чтобы представить скорость дрейфа в векторном виде, надо составить из векторов h и H вектор, направленный вдоль оси x. Такой вектор имеет вид:

h, H . (I.4.23)

Кроме того, численный коэффициенто 1/ надо заменить на точный коэффициент 1/2. Окончательно получаем:

то выражение (I.4.24) сводится к cкорости дрейфа, описываемой первым членом выражения (I.4.17) c

47

силой (I.4.25).

На основе дрейфовой теории легко качественно понять природу одной из наиболее важных неустойчивостей в магнитных ловушках, так называемой "желобковой моды". Рассмотрим поведение плазмы в пробкотроне. Пусть плотность плазмы спадает от оси системы, а магнитное поле направлено за плоскость чертежа на рис. 9. Этот рисунок показывает сечение пробкотрона, соответствующее плоскости, перпендикулярной оси системы и проходящей через точку 0. Представим, что по случайным причинам желобок более плотной плазмы проник в область более низкой плотности, как это показано на рис. 10.

В среднем сечении пробкотрона градиент модуля магнитного поля направлен к оси, т.е. в направлении, противоположном направлению выпуклости силовых линий. Тогда, согласно (I.4.23), положительно заряженные частицы будут дрейфовать против часовой стрелки и накапливаться на левой границе желобка. Отрицательно же заряженные − в противоположном направлении и накапливаться на правой границе. Это приведет к возникновению электрического поля, направленного по часовой стрелке. Под действием этого поля все частицы, согласно (I.4.18), будут удаляться от центра. Однако частицы не остаются в центральной области, а колеблются между пробками. В области, соответствующей т. 1 на рис. 6, градиент модуля поля имеет направление от центра, и частицы под действием электрического поля будут дрейфовать к центру.

48

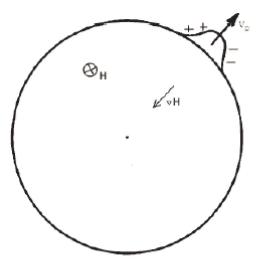
Рис. 10. Развитие желобка

Можно показать, что в пробкотроне суммарное смещение частиц направлено от центра, и желобок в целом будет всплывать, т.е. плазма неустойчива. Для обеспечения устойчивости на поле пробкотрона можно наложить дополнительные внешние поля, как это делается в установке Иоффе, иначе говоря, пробкотроне со стабилизирующими стержнями. Подробнее об этом см. книгу [6].

49

Глава II. Описание стационарного магнитного поля в ловушках.

II.1. Основные понятия

В этом разделе мы рассмотрим основные понятия, относящиеся к геометрии магнитного поля в стационарных магнитных ловушках. Уравнения, описывающие такие поля, − это уравнения Максвелла для стационарного случая. Токи в плазме мы будем учитывать явно. В этом случае векторы H и B не различаются. Поэтому можно написать:

50