
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf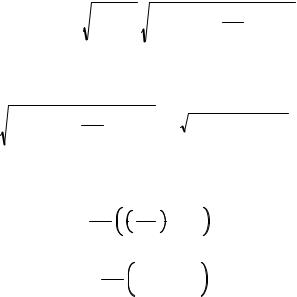
(III.8) можно |
решать в приближении r const. Это |
||||
приближение |
становится несправедливым |
вблизи |
|||
магнитной оси. |
|
||||
Член, |
r |
|
cos в первых скобках даёт |
лишь |
|
R0 |
|||||
|
|
|
|||
малую поправку, и его можно опустить. Под знаком корня члены нулевого порядка могут скомпенсировать друг друга, и такой член необходимо сохранять. Тогда можно написать:
d |
1 |
|
H0r |
mR0v2 |
|
R0 |
− cos . |
(III.10) |
|
|
|
|
|
|
H0r |
− |
r |
||
dt |
R0q |
mR0 |
|||||||
Выражение под корнем можно представить так:
mR0v2 |
|
− |
R0 |
− cos |
≡ |
2 |
2 |
− 1 |
− cos , |
|
|||
H0r |
|
r |
|
|
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
R0 |
|
v |
2 |
− 1 |
|
1 |
|
(III.11) |
||
|
|
r |
|
v |
|
|
|
||||||
|
|
|
|
R0 |
mv2 |
− 1 |
|
1. |
|
|
|||
|
|
|
|
r |
H0 |
|
|
|
|
||||
Можно найти |
|
точное |
|
|
решение |
уравнения |
|
||||||
(III.10). Оно выражается через полные эллиптические интегралы и не является достаточно наглядным. Поэтому рассмотрим наглядные предельные случаи. На внутреннем обводе тора поле сильнее, чем на внешнем. Поэтому частицы,
81

двигаясь почти по силовой линии, могут отражаться от области сильного поля, либо проходить сквозь неё аналогично тому, как это происходит в пробкотроне.
1. Быстропролётные частицы.
Это частицы, у которых v v . Они почти не тормозятся на внутреннем обводе тора. Из (III.11) видно, что для них 1. В этом пределе уравнение для упрощается:
d |
|
v |
, |
(III.12) |
|
dt |
R0q |
||||
|
|
|
откуда
− 0 Rvq t − t0 .
0
Период полного оборота по полоидальному углу
составляет
2 Rv 0q .
(III.13)
(III.14)
2. Глубоко запертые частицы.
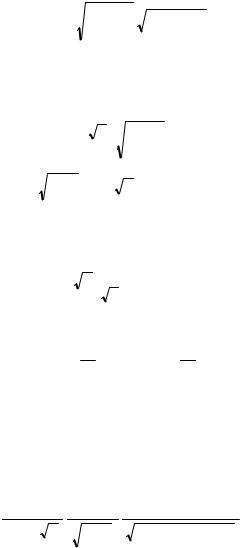
Рассмотрим теперь противоположный предельный случай, т.е. глубоко запертые частицы. Для таких частиц на всей траектории v /v 1. Они сосредоточены на внешнем обводе тора, мало отклоняясь от экваториальной плоскости, т.к. легко отражаются от области сильного поля. Введём новый угол − 1. Тогда cos ≈ −1 2/2, а вместо (III.11) имеем:
82
|
d |
|
|
1 |
|
|
|
H0r |
4 2 − 2 . |
|||||||
|
|
|
R0q |
|
|
|
2mR0 |
|||||||||
|
dt |
|
|
|
|
|
|
|||||||||
Это уравнение |
легко |
интегрируется |
||||||||||||||
элементарных функциях: |
|
|
|
|||||||||||||
|
|
− 0 |
|
|
|
|
|
|
|
H0 |
|
|||||
arcsin |
|
|
|
|
|
|
|
|
|
|
t |
− t0 . |
||||
|
2 |
|
R0q |
|
2m |
|||||||||||
Заметим, |
что |
|
|
H0 |
|
|
≈ v/ 2 . Т.к. |
sin /2 |
||||||||
|
|
2m |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(III.15)
в
(III.16)
не
может превосходить единицы, движение является периодическим с периодом
2 2 |
R0q |
. |
(III.17) |
|
|||
|
v |
|
|
Обратную величину называют баунс-частотой.
В точках поворота arcsin 2 /2, т.е. 2 1.
Рассмотрим теперь отклонение частиц от магнитной поверхности r. Удобно решать не уравнение (III.9), а разделить его на уравнение
(III.10). Считая r r и схраняя член |
r |
cos |
|
||
|
R0 |
|
лишь там, где он важен, т.е. только под знаком корня, получаем уравнение для r :
d r |
|
mcq |
v2 v2 |
sin |
. |
(III.18) |
||
d |
2eH0 |
|
H0 |
|
||||
|
|
|
2 2 − 1 − cos |
|
|
|||
|
|
mv |
|
|
||||
|
|
|
|
|
|
|
||
83

Это уравнение легко интегрируется в
элементарных функциях.
Для быстропролётных частиц v ≈ v, 1. В результате получаем:
d r |
mcv q cos , |
r − r0 |
|
|
d |
||||
eH0 |
|
|
mcv q cos − 0 . eH0
Максимальное смещение составляет величину
rmax q.
(III.19)
(III.20)
Так как в средней части разряда q обычно порядка нескольких единиц, то смещение быстропролётных частиц от магнитной поверхности оказывается порядка нескольких ларморовских радиусов
Для глубоко запертых частиц это смещение
оказывается существенно больше. Непосредственно интегрируя (III.18) и полагая v v, получаем:
r |
|
mcv |
|
q 2 2 |
− 1 − cos . |
(III.21) |
|
eH0 |
|
|
|
||
Максимальное |
смещение |
достигается |
при |
|||
cos −1. Кроме того, для глубоко запертых частиц→ 1. Следовательно,
84

|
rmax |
2 |
mcv |
q. |
(III.22) |
||
|
|
|
|
eH0 |
|
|
|
Сравнивая эту величину со смещением |
|||||||
быстропролётных частиц (III.20), видим, что оно |
|||||||
отличается |
не |
только |
малозначительным |
||||
множителем |
2 , |
но и |
малой |
величиной |
в |
||
знаменателе. Т.е. смещение запертых частиц |
|
||||||||||||||
существенно превышает ларморовский радиус. |
|
||||||||||||||
Из выражения (III.21) видно, что проекция |
|
||||||||||||||
траектории запертой частицы на сечение const |
|
||||||||||||||
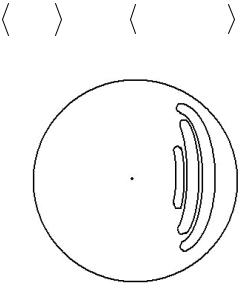
по форме напоминает банан (см. рис. 19.). Поэтому |
|
||||||||||||||
такие траектории называют банановыми, а режим |
|
||||||||||||||
столкновений, при котором частицы успевают |
|
||||||||||||||
замкнуть банановую траекторию, ни разу не |
|
||||||||||||||
столкнувшись с другой частицей, называют |
|
||||||||||||||
банановым. Напомним, что "бананы" на рисунке - |
|
||||||||||||||
это только |
|
проекции |
траекторий |
на плоскость |
|
||||||||||
const. На самом деле банановые траектории не |
|
||||||||||||||
являются замкнутыми |
вследствие |
тороидального |
|
||||||||||||
смещения частиц. Рассмотрим тороидальную |
|
||||||||||||||
компоненту уравнения (III.4) для глубоко запертых |
|
||||||||||||||
частиц: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
d |
|
h v |
|
mcv2 |
h, H e |
(III.23) |
|||||||
|
dt |
||||||||||||||
|
|
|
|
2eH0 |
|
|
|
|
|
|
|||||
и усредним его по банановым осцилляциям. В |
|
||||||||||||||
первом приближении h v 0. |
|
|
|||||||||||||
R0 |
|
d |
|
mcv2 |
|
H |
|
|
H0 |
|
cos . |
|
|||
|
dt |
2eH02 H0 |
|
|
R0 |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||
85
Напомним, что "бананы" на рисунке это только проекции траекторий на плоскость const. На самом деле банановые траектории не являются замкнутыми вследствие тороидального смещения частиц. Рассмотрим тороидальную компоненту уравнения (III.4) для глубоко запертых частиц:
R0 |
d |
h v |
mcv2 h, H e |
(III.23) |
|
dt |
|||||
|
|
2eH0 |
|
и усредним его по банановым осцилляциям. В первом приближении h v 0.
R0 |
d |
|
mcv2 |
H |
|
H0 |
cos . |
dt |
2eH02 |
H0 |
|
R0 |
|||
|
|
|
|
Рис. 19. Банановые траектории
86

Для глубоко |
запертых частиц |
cos ≈ −1. |
|||
Окончательно имеем: |
|
|
|
|
|
R0 |
d |
|
|
v. |
(III.24) |
dt |
2qR0 |
||||
Заметим, что направление тороидального дрейфа зависит от знака заряда (в окончательной формуле заряд вошел в ), т.е. вследствие этого дрейфа в тороидальной плазме течёт ток. Однако в плазме за счет тороидальности и столкновений течет гораздо более сильный ток, называемый бутстреп-током. Действительно, из-за градиента плотности в точку на "экваторе" (см. рис.19) приходят запертые частицы из более плотных областей, а из менее плотных областей − с
противоположными направлениями |
скоростей. |
|||||||
Число таких частиц отличается на величину |
dntr |
, |
||||||
dr |
||||||||
где − ширина банана, ntr − плотность запертых |
||||||||
частиц. Средняя квадратичная параллельная |
||||||||
скорость для них по порядку величины равна |
vT, |
|||||||
где vT − тепловая скорость. Поэтому ток запертых |
||||||||
частиц определяется так: |
|
|
|
|
|
|
|
|
jbanana −ev |
dntr |
− |
3/2 1 |
dP |
. |
|
(III.25) |
|
dr |
|
H |
dr |
|
||||
|
|
|
|
|
|
|||
Здесь Р − давление плазмы. Для пролётных частиц радиальное смещение мало, и их током можно было бы пренебречь, если бы они не увлекались запертыми частицами за счет столкновений. Для электронов баланс сил можно представить в виде
87

nemevuntrap ei eemejbanana/e. |
(III.26) |
Слева здесь сила, описывающая торможение
пролётных электронов ионами, справа − сила, действующая на пролетные электроны со стороны
запертых и ускоряющая их, ei и ee − соответствующие частоты столкновений.
Электронные столкновения переводят пролётные частицы в захваченные. Частота таких столкновений в 1 раз больше. Окончательно
jboots |
−e1/2 |
1 |
dP |
, |
(III.27) |
|
H |
||||||
|
|
dr |
|
|
||
т.е. jboots в 1/ раз больше, |
чем |
ток |
запертых |
|||
частиц.
До сих пор мы не учитывали влияния электрического поля. Однако в токамаке всегда присутствует индукционное электрическое поле, поддерживающее тороидальный ток (за исключением токамаков с безындукционным поддержанием тока).
Рассмотрим сначала его влияние на пролетные частицы. Оно приводит к ЕхВ дрейфу в радиальном направлении:
vE |
с |
E, H er. |
(III.28) |
|
H2 |
||||
|
|
|
Такой дрейф всегда направлен к центру, т.е.
индукционное поле "поджимает" разряд.
88
Действительно, пусть индукционное поле направлено вдоль тороидального поля. В этом же направлении течет и тороидальный ток. Создаваемое им полоидальное поле направлено против часовой стрелки, и векторное произведениеE, H и, соответственно, дрейфовая скорость направлены к магнитной оси. Пусть индукционное
электрическое поле направлено теперь против поля тороидального. При этом направление создаваемого им полоидального магнитного поля также поменяло направление. Векторное же произведение E, H и, следовательно, дрейфовая скорость направления не изменили, т.е. по-прежнему направлены к магнитной оси.
На запертые частицы индукционное электрическое поле влияет гораздо сильнее. В отсутствие такого поля точки отражения симметричны относительно экваториальной плоскости токамака, и смещение запертой частицы вдоль малого радиуса наружу на одной части траектории в точности компенсируется на другой ее части. Индукционное поле имеет параллельную составляющую, которая ускоряет частицы в продольном направлении, если параллельная скорость совпадает с ней по направлению, и тормозит в противоположном случае. Таким образом, точки поворота становятся несимметричными, и дрейфы в радиальном направлении друг друга компенсируют не полностью. Рассмотрим этот эффект количественно. Выразим индукционное поле через
89
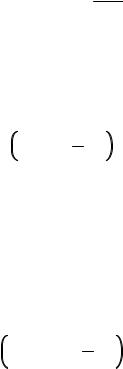
векторный потенциал: |
|
|
|
|
E |
− |
∂A |
. |
(III.29) |
∂t |
В силу тороидальной симметрии лагранжиан
частицы не зависит от тороидальной координаты , и соответствующий обобщенный импульс ∂L/∂ (III.1.3) сохраняется:
R |
|
e |
A |
const. |
(III.30) |
|
|||||
mR c |
|||||
В токамаке тороидальное поле много больше полоидального, поэтому тороидальную ссоставляющую скорости можно представить как проекцию на тороидальное направление параллельной скорости v B /B плюс малую осциллирующую добавку от проекции перпендикулярной скорости. Усредним (III.30) по ларморовскому периоду. В результате получим:
|
|
R mv |
B |
|
e |
|
|
|
|
|
|
|
|
|
|
c |
A |
|
const. |
(III.31) |
|||
|
B |
||||||||||
В |
e |
точке |
поворота |
|
|
v 0, |
т.е. |
||||
∂L/∂ |
RA . Спустя |
|
период |
частица |
снова |
||||||
c |
|
||||||||||
окажется в точке поворота, но уже с новыми |
|||||||||||
координатами. При этом величина ∂L/∂ , |
|||||||||||
естественно, не изменится, |
|
e |
RA 0. С другой |
||||||||
c |
|||||||||||
стороны, изменение этой величины можно |
|||||||||||
представить в виде суммы первых членов |
|||||||||||
разложения в ряд по r |
и |
t, |
где t − период |
||||||||
обращения частицы по "банану":
90
