
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf
Глава IX. Электромагнитные волны в плазме
IX.1. Электромагнитные волны в незамагниченной плазме
Ранее мы анализировали сравнительно низкочастотные волны в плазме: МГД-волны, ленгмюровские и др. При этом мы в уравнениях
Максвелла пренебрегали током смещения ∂∂Еt . В
этом разделе мы рассмотрим высокочастотные волны, для чего будем изучать полные уравнения Максвелла:
rot E − |
1 |
∂H |
, |
|
|
|
(IX.1.1) |
|
c |
|
∂t |
|
|
∂E |
|||
rot H |
4 |
j |
1 |
|
, |
|||
|
c |
|
||||||
|
c |
|
|
|
|
∂t |
||
div E 4 , div H 0.
Уравнения Максвелла должны быть также дополнены материальными уравнениями. Одним из них является уравнение непрерывности для тока:
div j − |
∂ |
. |
(IX.1.2) |
|
|||
|
∂t |
|
|
Введем вектор P, такой, что
191

∂P/∂t 4 j. |
(IX.1.3) |
Тогда из уравнения непрерывности электрического заряда получаем:
div P −4 . |
(IX.1.4) |
Подставляя (IX.1.4) в (IX.1.1), получаем:
rot H |
1 |
|
∂P |
|
∂E |
. |
(IX.1.5) |
c |
∂t |
|
|||||
|
|
|
∂t |
|
|||
Из (IX.1.1) и (IX.1.4) видно, что div E −div P.
Введем вектор электрической индукции
D P E. |
(IX.1.6) |
Тогда два из уравнений (IX.1.1) можно переписать так:
rot H 1 ∂D , c ∂t
div D 0.
Скорости частиц, а, следовательно, и вектор P, называемый вектором поляризации, линейно связаны с электрическим полем:
(IX.1.7)
(IX.1.8)
P E , D E . |
(IX.1.9) |
Здесь − символ Кронекера. В изотропной плазме − диагональный тензор, .
Введем также тензор диэлектрической проницаемости
192
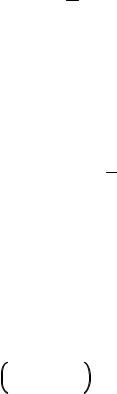
. |
(IX.1.10) |
В изотропной плазме .
Воздействуя оператором rot на уравнение (IX.1.7), получаем в операторном виде:
H |
1 |
|
|
|
, |
∂D |
|
|
(IX.1.11) |
||||||
|
|
|
|
||||||||||||
|
c |
|
|
|
|
|
|
|
|
|
|
||||
|
|
∂t |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Левую часть уравнения (IX.1.11) можно |
|
||||||||||||||
представить в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H − H , H . |
(IX.1.12) |
||||||||||||||
Последний член в (IX.1.12) обращается в ноль. |
|
||||||||||||||
Правая часть (1.11) преобразуется так: |
|
||||||||||||||
rot D rot E − |
|
|
|
∂H |
|
||||||||||
c |
|
|
|
. |
(IX.1.13) |
||||||||||
|
∂t |
||||||||||||||
Подставляя (IX.12) и (IX.13) в (IX.11), получаем |
|
||||||||||||||
окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
∂2H |
(IX.1.14) |
|||||||||
|
c2 |
|
|
∂t2 |
|
|
|
|
|
|
|||||
Для того, чтобы получить дисперсионное уравнение, связывающее частоту и волновой вектор, перейдем к фурье-представлению:
k2 − |
|
2 H 0. |
(IX.1.15) |
|
c2 |
||||
|
|
|
||
Уравнение (IX.1.15) |
имеет |
нетривиальное |
||
решение только в том случае, если
193

k2 − c2 2 0.
Уравнение (IX.1.16) и является дисперсионным уравнением для электромагнитных волн в однородной незамагниченной плазме.
Решением этого уравнения является выражение
kc .
Двойной знак означает, что волна может распространяться в двух взаимно противоположных направлениях.
Для высокочастотных волн, kvTe, как было уже показано,
1 − 2p/ 2.
(IX.1.16)
(IX.1.17)
(IX.1.18)
Если p, то 0, Re 0. Следовательно, волна с такой частотой распространяться не может. Пусть извне на неоднородную плазму падает электромагнитная волна, длина которой много меньше характерного размера неоднородности. Очевидно, что плазменная частота р по мере
углубления в плазму растёт с ростом плотности. Следовательно, такая волна должна отразиться от поверхности, на которой плазменная частота начинает превышать частоту волны. Это не значит, что возмущения вовсе не проникают глубже этой поверхности. На самом деле электромагнитная волна вблизи поверхности частично трансформируется в собственные колебания плазмы.
194

Заметим, что для рассматриваемых волнвсегда меньше единицы, и фазовая скорость всегда больше скорости света. Естественно, что это не противоречит теории относительности, так как информация переносится не с фазовой, а с групповой скоростью, которая не превосходит скорость света.
vgr ≡ |
∂ |
c |
kc |
c. |
|
∂k |
|||||
|
|
k2c2 − p2 |
|
IX.2. Электромагнитные волны в замагниченной плазме
Если в незамагниченной плазме не было выделенного направления, то в замагниченной плазме такое направление существует. Поэтому диэлектрическая проницаемость такой плазмы – это тензор, а набор волн, распространяющихся в ней, значительно богаче.
Вернемся к уравнениям Максвелла и перепишем их в фурьепредставлении:
k, E |
|
H. |
(IX.2.1) |
||
c |
|||||
k, H − |
|
D. |
(IX.2.2) |
||
c |
|
||||
k, D 0. |
|
|
(IX.2.3) |
||
195
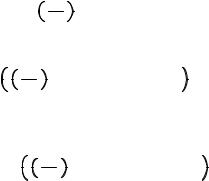
k, H 0.
Подставим H из (IX.2.1) в (IX.2.2) и раскроем двойное векторное произведение
2D k2E − k k, E , c
или в компонентах
2 |
− k |
2 |
k k |
E |
0. |
c |
|
Эта система уравнений имеет нетривиальные решения, если ее детерминант обращается в ноль:
det |
2 |
− k |
2 |
k k |
0. |
c |
|
(IX.2.4)
(IX.2.5)
(IX.2.6)
Аналогичная ситуация возникает в кристаллооптике. Там уравнение (IX.2.6) называют уравнением Френеля.
Вычислим в холодной магнитоактивной плазме, т.е. будем считать, что kvTe. В этом случае можно пренебречь такими кинетическими эффектами, как затухание Ландау, и производить вычисления в гидродинамическом приближении.
Разобьем поляризацию на электронную и ионную части, P Pe Pi. Из уравнения (IX.1.3) для каждой из них имеем:
− i Pj 4 jj 4 ZjnjVj, |
(IX.2.7) |
откуда находим вектор поляризации
196

P ∑Pj; |
Pj 4 i |
Zjenj |
Vj. |
(IX.2.8) |
|
j
Здесь индекс j означает сорт частиц, j e, i. Zj означает знак заряда частицы. Мы будем
рассматривать |
простую |
|
|
электрон-протонную |
||||||||||
плазму: Zi 1, Ze |
−1. Vj |
|
_ коллективная скорость |
|||||||||||
частиц. |
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем скорости из уравнений движения |
|
|
|
|||||||||||
|
∂Vj |
|
Zje |
1 |
|
|
|
|
||||||
|
|
|
|
|
|
mj |
E |
c |
Vj, H , |
|
|
(IX.2.9) |
||
|
∂t |
|
|
|
|
|||||||||
или, в фурье-представлении, |
|
|
|
|||||||||||
− i Vj |
|
|
Zje |
|
E Hj Vj, h . |
|
|
(IX.2.10) |
||||||
|
mj |
|
|
ZjeH |
||||||||||
Здесь введены ларморовские частоты Hj |
|
|
||||||||||||
mjc |
||||||||||||||
и единичный вектор h H/H, направленный вдоль магнитного поля.
Пусть система координат выбрана так, что ось z направлена вдоль магнитного поля. Тогда систему (IX.2.10) можно переписать в компонентах так:
i Vjx |
Zje |
Ex HjVjy, |
(IX.2.11) |
mj |
|||
i Vjy |
Zje |
Ey − HjVjx, |
(IX.2.12) |
mj |
197

i Vjz |
Zje |
Ez. |
(IX.2.13) |
mj |
Уравнение (IX.2.13) содержит только z-компоненту скорости, а (IX.2.11) и (IX.2.12),
напротив, ее не содержат. Таким образом, она отщепляется. Выразим скорости через электрическое поле с помощью (IX.2.11) _ (IX.2.13) и подставим (IX.2.8). Используя условие квазинейтральности ni ne ≡ n, получаем:
Px i ∑ |
pj |
|
i Ey HjEx |
, |
(IX.2.14) |
||||
|
|
|
|
2 |
2 |
||||
j |
|
|
|
|
|
− Hj |
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Py i ∑ |
pj |
|
HjEy i Ex |
, |
(IX.2.15) |
||||
|
|
|
|
2 |
2 |
||||
j |
|
|
|
|
|
− Hj |
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pz − ∑ |
pj |
|
|
2Ez. |
|
(IX.2.16) |
|||
|
|
|
|
||||||
|
|
|
|
j |
|
|
|
|
|
Пользуясь этими соотношениями и связью между P и E (IX.1.9), (IX.1.10), находим компоненты тензоров и :
хх хх − ∑ |
|
|
pj2 |
, |
xx yy |
(IX.2.17) |
|
2 |
2 |
||||
j |
|
− Hj |
|
|
||
|
|
|
|
|
|
|
198
1 −∑ |
|
|
|
pj2 |
|
|
, |
|
|
|
|
|
||||||||
|
|
2 |
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
j |
|
|
|
− Hj |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zz − ∑ |
|
pj2 |
; zz |
1 |
− |
|
∑ |
|
pj2 |
. |
(IX.2.18) |
|||||||||
|
2 |
|
|
2 |
||||||||||||||||
j |
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В этом выражении обычно можно пренебречь |
|
|||||||||||||||||||
членом, пропорциональным |
pi2 , |
|
и пользоваться |
|
||||||||||||||||
выражением zz 1 |
− |
|
p2е |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy − yx |
i |
∑ |
|
|
|
pj2 Hj |
|
, |
|
(IX.2.19) |
||||||||||
|
|
|
2 |
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
j |
|
|
|
− Hj |
|
|
|||||||
xy xy − yx, |
|
|
|
|
|
|
|
|||||||||||||
zx |
zx |
xz |
zx |
|
|
|
(IX.2.20) |
|||||||||||||
zy |
zy |
yz |
yz 0. |
|
|
|
|
|||||||||||||
Введя |
|
xy ≡ ig, |
|
|
|
|
|
|
обозначения |
|
||||||||||
xx ≡ , zz ≡ , |
|
|
|
|
запишем |
тензор |
|
|||||||||||||
диэлектрической проницаемости в виде
199

|
|
|
ig |
0 |
|
|
|
|
−ig |
|
0 |
. |
(IX.2.21) |
00
Влитературе иногда также встречаются обозначения: ≡ ; ≡ .
Заметим, что все компоненты этого тензора не
зависят от волнового вектора.
Итак, теперь мы можем выразить все коэффициенты в дисперсионном уравнении (IX.2.6) через и k. После простых, но громоздких вычислений можно получить:
A |
|
kc |
4 B |
|
kc |
2 C 0. |
(IX.2.22) |
|
|
|
|
||||
|
|
|
|
|
|||
Здесь |
sin2 cos2 , B − 1 cos |
||||||
A k−2 k k |
|||||||
|
|
|
|
|
угол |
между |
|
C 2 − g2 , kH0 |
− |
||||||
направлениями |
|
волнового |
вектора и магнитного |
||||
поля.
Так как функции A, B и C, так же, как и тензор, не зависят от волнового вектора, решение биквадратного уравнения (IX.2.22) позволяет найти зависимость фазовой скорости /k от частоты. Уравнение (IX.2.22) биквадратное, поэтому имеются два решения для квадрата фазовой скорости, т.е. два типа волн.
В общем случае выражение для фазовой скорости очень громоздко, поэтому рассмотрим некоторые частные случаи.
200
