Морозов Введение в теорию горячей плазмы Ч.1 2011

eс 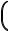r ∂∂r RA t ∂∂t RA 0.

Здесь Bp − полоидальное поле. Положим также,

что ∂∂t RA ≈ R ∂∂At .

Используя (III.30), (III.32) и (III.34), получаем:

Легко видеть, что банан под действием индукционного поля смещается к центру, причем скорость его смещения превышает в B/Bp 2 раз

91

скорость смещения пролетной частицы.

Таким образом, индукционное электрическе поле поджимает разряд к магнитной оси. Это явление по имени открывателя называется вейровским (иногда уэйровским) пинчем.

Глава IV. Плазма как сплошная среда. Кинетическое описание

IV.1. Заряд в плазме. Дебаевская экранировка

До сих пор мы рассматривали движение отдельных частиц в электрических и магнитных полях. Однако в большинстве случаев плазма ведёт себя как целый ансамбль частиц, которые взаимодействуют между собой посредством электрических и магнитных полей. Если характерный размер задачи много больше среднего расстояния м ежду частицами 1/n 3, то совокупность заряженных частиц следует рассматривать как некую сплошную среду, проявляющую свойства, которые трудно описать в приближении отдельных частиц. В этом случае пришлось бы рассматривать необозримое число

92

объектов. В то же время такая среда обладает некими усреднёнными характеристиками, которые возможно описать. С подобным описанием читатель уже сталкивался в статистической физике.

В качестве примера рассмотрим пробную частицу с зарядом Ze, помещенную внутрь смеси из электронов и ионов, т.е. в плазму, причем эта плазма в отсутствие пробного заряда является нейтральной. Это значит, что невозмущённые концентрации электронов и ионов равны, n0e n0i . Рассмотрим, какие поля возникают в плазме вокруг неподвижного пробного заряда в неподвижной плазме.

В этом случае электростатическое поле описывается уравнением

где e ni − ne − плотность электрического заряда, магнитное поле не возникает, а электрическое поле можно описать с помощью электростатического потенциала, E − . Тогда уравнение (IV.1.1) можно переписать в виде:

начала координат, куда мы помещаем пробный заряд Ze.

Для простоты будем считать, что заряд иона плазмы и заряд электрона по модулю равны. Каждый из них в электрическом поле будет иметь энергию e и − e соответственно. Тогда, согласно

93

Здесь мы использовали так называемое условие квазинейтральности, т.е. положили ni ne n.

Задача имеет сферическую симметрию. Следовательно, удобно воспользоваться сферической системой координат. Так как при сферической симметрии функция не зависит от углов, соответствующие производные в лапласиане выпадают, и уравнение (IV.1.4) принимает следующий вид:

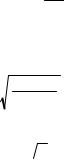
дополнить граничными условиями. В центре потенциал должен совпадать с потенциалом точечного заряда Ze. Следовательно,

94

На бесконечности же можно положить

0 при r → .

Решение такой краевой задачи хорошо известно:

где величина

называется радиусом Дебая. (Иногда радиусом Дебая называют величину в 2 раз меньшую.)

Таким образом, на расстоянии порядка rD потенциал, создаваемый пробным зарядом, экранируется.

IV.2. Кинетическое уравнение

Как известно, систему из многих частиц можно описать с помощью плотности частиц в фазовом пространстве f r, p . По-другому она называется функцией распределения. Плотность и ток частиц выражаются через функцию

95

распределения следующим образом:

Если не принимать во внимание процессы рождения-поглощения частиц, то можно сказать, что плотость частиц в фазовом пространстве должна сохраняться, т.е.

Это равенство известно как теорема Лиувилля. Полную производную по времени можно

раскрыть следующим образом:

действующие на частицу, с помощью уравнений движения:

Под электрическими и магнитными полями

96

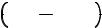
здесь подразумеваются поля, создаваемые как внешними источниками, так и всеми частицами плазмы в точке наблюдения (исключая, естественно, самодействие). Поля эти точно вычислить невозможно, поэтому их разбивают на две части: усреднённые поля и поля отдельных частиц, которые отличаются от усреднённых лишь на малых расстояниях от частицы. Тогда взаимодействие данной частицы с остальными можно разделить на движение в усреднённых полях и столкновения, т.е. мгновенный переброс частицы из данной области фазового пространства в какую-то другую, и этот переброс учитывается в виде так называемого интеграла столкновений, который обычно обозначается как St. Для рассматриваемых нами проблем с большой степенью точности можно ограничиться только парными столкновениями. С учётом сказанного выше уравнение (IV.2.5) можно переписать в виде:

Здесь под E и Н понимаются уже усредненные поля. Уравнение (IV.2.6) называют кинетическим. В горячей плазме во многих случаях характерные времена рассматриваемых процессов оказываются существенно меньше, чем времена между столкновениями, st −st1. Тогда столкновительным членом можно пренебречь. Такое уравнение называют бесстолкновительным кинетическим уравнением, или уравнением Власова.

97

Интеграл столкновений имеет весьма сложную форму. Поэтому, когда столкновения можно учесть лишь качественно, используют т.н. - приближение:

Здесь f0 − функция распределения, обращающая интеграл столкновений в ноль. Часто в качестве такой функции можно взять функцию Максвелла. К сожалению, такое приближение плохо тем, что не сохраняет числа частиц. Это легко видеть, проинтегрировав по dp уравнение (IV.2.5) с интегралом столкновений в форме (IV.2.7).

IV.3. Ленгмюровские волны

Рассмотрим распространение слабых электростатических возмущений в незамагниченной плазме. Для этого рассмотрим, как возмущается функция распределения под действием электрического поля. Мы здесь не будем конкретизировать вид частиц. Воспользуемся методом линеаризации кинетического уравнения. Это значит, что мы будем представлять функцию распределения в виде f0 f, где f f0 − малая

добавка к равновесной функции распределения f0. Пусть равновесная функция распределения не зависит от времени и однородна в пространстве, т.е. ∂f0/∂t 0, f0 0. В невозмущённом состоянии

98

положим E H 0. Положим также, что плазма в невозмущённом состоянии неподвижна. Столкновения будем считать слабыми и запишем столкновительный член в − приближении. Тогда уравнение в нулевом приближении удовлетворяется тождественно. В первом приближении (мы сохраняем только линейные по f, E и H члены, квадратичные члены типа E f выбрасываем) уравнение (IV.2.6) принимает вид:

Уравнение (IV.3.1) − линейное, поэтому его решение можно искать с помощью Фурье-анализа,

f fk. exp −i t ikr . Под величинами E и H мы

теперь будем пониматьфурье-образы полей. Фурье-образ уравнения (IV.3.1) имеет вид:

− fk, ,

откуда легко находим вид возмущённой части функции распределения:

Для решения нашей задачи кинетическое уравнение должно быть дополнено уравнениями

99

100