
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf
Подставляя (II.1.2) во второе уравнение (II.1.1),
с учетом (II.1.3), легко получаем: |
|
|
|
||||||
A − |
4 |
j. |
|
|
(II.1.4) |
||||
c |
|
|
|||||||
Решение этого уравнения хорошо известно: |
|
||||||||
A |
1 |
|
j r′ dV′ |
, |
(II.1.5) |
||||
с |
|
R |
|
||||||
и, как следствие, |
|
|
|
|
|
|
|
|
|
H |
1 |
|
j, R dV′ |
|
. |
(II.1.6) |
|||
с |
|
R3 |
|
||||||
Здесь R r − r′ − вектор, соединяющий точку внутри объёма интегрирования с точкой наблюдения, dV′ dx′dy′dz′ − элемент объёма.
Силовая линии - это линия, касательная к которой в каждой её точке совпадает по направлению с вектором H. Уравнения силовых линий в декартовой системе координат имеют вид:
dx |
|
dy |
|
dz |
. |
(II.1.7) |
Hx |
|
|
||||
|
Hy |
Hz |
|
|||
Уравнения силовых линий могут быть представлены в гамильтоновой форме. (Подробно об этом можно прочитать в книге А.А. Сковорода. Магнитные ловушки для удержания плазмы. Москва, Физматлит, 2009 г.) Проще всего это представление можно получить в случае
двумерного поля H Hx x, y ; Hy x, y , H0 , где H0 const. Векторный потенциал такого поля
51

имеет вид: |
|
A −H0y, 0, Az x, y . |
(II.1.8) |
Введем новую переменную t H0z. |
Тогда |
уравнения (II.1.9) можно представить в виде: |
|
|
(II.1.9) |
x Hx, |
|
|
|
y Hy. |
|
Если выразить поле через векторный потенциал (II.1.8) и ввести гамильтониан H Az, то эти уравнения преобразуются к гамильтоновой форме:
|
|
||
x |
∂∂Hy |
, |
(II.1.10) |
y − ∂∂Hx . |
|
||
|
|
||
Магнитный поток через поверхность S |
|
||
определяется следующим образом: |
|
||
H dS. |
(II.1.11) |
||
Полезно ввести понятие магнитной трубки. Это трубка, поперечный размер которой много меньше размера, на котором существенно меняется магнитное поле, а поверхность устроена так, что её не пересекают силовые линии. Можно также ввести удельный объём такой трубки:
U |
V |
. |
(II.1.12) |
|
|||
|
|
|
|
Здесь V − объём трубки, а - поток через её
52
сечение. Если l - координата вдоль силовой линии, то (II.1.12) можно переписать так:
|
U |
dS dl |
. |
|
|
(II.1.13) |
|||
|
|
|
|||||||
|
|
|
H dS |
|
|||||
Но внутри трубки H dS const, а векторы dS |
|
||||||||
и dl совпадают по направлению. Тогда выражение |
|
||||||||
(II.1.13) можно переписать так: |
|
||||||||
|
dSdl |
|
|||||||
U |
|
|
dl |
|
dl |
. |
(II.1.14) |
||
HdS |
H |
B |
|||||||
Нахождение магнитного поля и его силовых линий значительно упрощается в областях, где отсутствуют токи, в частности, в вакууме. В таких областях rotH 0, и можно ввести скалярный магнитный потенциал M, такой, что
B − M. |
(II.1.15) |
При этом область, в которой это представление
справедливо, должна иметь определенные свойства. Через поверхность, натянутую на произвольный замкнутый контур в этой области, не должен протекать ток. В противном случае она должна быть разрезана. Рассмотрим, например, поле тороидального соленоида. Любая силовая линия в таком соленоиде замкнута, и через поверхность, натянутую на круговую силовую линию, протекает ток, локализованный на обмотке. В этом случае объем тора должен быть рассечен плоскостью,
53

перпендикулярной силовым линиям, а скалярный потенциал будет иметь на разрезе скачок.
Задача
Вычислить скалярный потенциал магнитного диполя.
Решение
Векторный потенциал магнитного диполя (см. формулу (I.1.8)) имеет одну компоненту A sin . Компоненты магнитного поля
выражаются через A :
Hr |
1 |
|
|
∂ A sin |
|
|
cos , |
|||
r sin |
∂ |
|
2 r3 |
|||||||
|
|
|
|
|||||||
|
1 |
∂ |
|
|
|
|
||||
H − |
r |
|
rA |
|
|
sin . |
|
|||
∂r |
4 r3 |
|
||||||||
Легко видеть, что для того, чтобы эти уравнения приняли вид H − M или в компонентах
Hr − ∂∂rM , H − 1r ∂∂ M ,
функция M должна иметь вид: M 4 r2 cos .
Зная скалярный потенциал диполя, можно рассчитать вакуумное поле от любого контура с током. Натянем на такой контур поверхность,
54
плотно заполненную магнитными диполями, токи в каждом из которых равны току в контуре. Все токи таких диполей внутри поверхности взаимно уничтожатся. Нескомпенсированными останутся лишь токи на границе. Скалярный потенциал поля, создаваемого контуром, будет равен сумме потенциалов отдельных диполей:
M |
cos |
d |
J |
|
cos |
dS. |
(II.1.16) |
2 |
4 |
2 |
|||||
|
4 R |
|
R |
|
|||
Здесь J − ток в контуре. Взяв градиент от
(II.1.16), получаем H. Такое вычисление часто оказывается значительно проще, чем вычисление по формуле Био-Савара-Лапласа.
II.2. Магнитные поверхности, коэффициент запаса устойчивости, шир
Во многих случаях магнитные силовые линии не располагаются в некоторм трёхмерном объёме, а лежат на двумерных магнитных поверхностях. В качестве примера рассмотрим круговой цилиндр с током, распределённым по радиусу и текущим вдоль его оси, совпадающей с координатной осью z. В цилиндрической системе координат r , , z вектор плотности тока имеет компоненты: j 0, 0, jz r Пусть также во всем пространстве существует однородное магнитное поле H0, также направленное вдоль оси z (см. рис. 11)
55
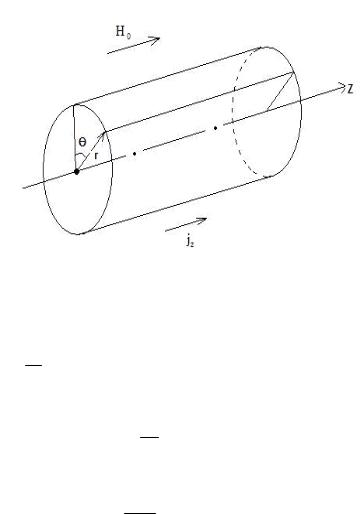
Рис. 11. Цилиндр с током
Cистема обладает цилиндрической симметрией. Поэтому, интегрируя уравнение rotH 4c j по поверхности, заключенной внутри окружности радиуса r с центром на оси системы, и используя теорему Стокса, имеем:
H |
2 |
jzdS. |
(II.2.1) |
cr |
Пусть весь ток сосредоточен на оси системы,
jz J |
r |
, |
jzdS J. |
(II.2.2) |
2 r |
Здесь J − полный ток в системе. Подставляя
56

(II.2.2) в (II.2.1), получаем:
H |
|
2J |
, |
(II.2.3) |
cr |
Пусть теперь ток равномерно распределен внутри цилиндра радиуса а и равен нулю вне его. В этом случае вместо (II.2.2) имеем:
H |
|
2Jr |
при r ≤ a, |
(II.2.4) |
|
ca2 |
|||||
|
|
|
|
||
H |
|
2J |
при r a. |
|
|
cr |
|
Здесь J jzdS − снова полный ток в системе.
Рассмотренная здесь модель является в ряде случаев хорошим приближением для токамака с малым отношением малого радиуса тора к большому, ≡ Ra . Величину называют
тороидальностью, а обратную величину − аспектным отношением. В таком торе можно положить R ≈ R0 const. Очевидно, что при обходе тора все физические величины должны быть периодичны. В частности, они должны совпадать на концах цилиндра при z 0 и z 2 R. Такое представление токамака называется цилиндром с отождествленными концами.
Введем очень важный и часто используемый параметр, который называется коэффициентом запаса устойчивости или коэффициентом Шафранова ( в зарубежной литературе он называется safety factor)
57
q |
r |
|
Hz |
. |
(II.2.5) |
R |
|
H |
|||
|
|
|
|
||
Впоследствии, когда |
|
будем |
рассматривать |
||
тороидальные эффекты, приводящие к нарушению цилиндрической симметрии, нам понадобится более общее определение.
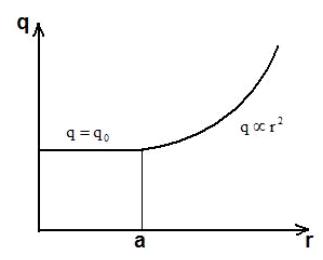
Рис. 12. Профиль q для равномерного распределения тока внитри цилиндра радиуса a.
Для случая тока, равномерно распределенного внутри цилиндра радиуса а, из (II.2.4) и (II.25) находим:
58

q |
ca2Hz |
q0 |
при r ≤ a, |
(II.2.6) |
||
2JR |
||||||
|
|
|
|
|||
q q0r2 |
при r a. |
|
||||
Этот профиль показан на рис. 12. Обычно в токамаке вблизи оси разряда величина q близка к единице и нарастает к периферии, но бывают случаи и немонотонного профиля q.
Задача
Найти профиль q при r a для следующего распределения тока:
jz j0 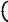 1 − ar
1 − ar 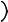 2.
2.
Решение
С помощью (II.1.17) находим:
|
2j0 |
|
|
r |
2 |
|
2 aj0 |
|
4 |
|
x2 |
||||||||||||
H |
cr |
2 rdr |
|
1 − |
a |
|
|
|
|
|
c |
x 1 − |
|
|
x |
|
. |
||||||
|
|
|
3 |
2 |
|||||||||||||||||||
Здесь |
x r/a. Подставляя |
|
это выражение в |
|
|
||||||||||||||||||
(II.1.21), получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
q |
cHz |
|
1 |
|
|
|
≡ q0 |
|
|
1 |
|
|
|
. |
|
|
|||||||
2 Rj0 |
|
1 − |
|
4 |
x |
x2 |
|
|
1 − |
4 |
x |
x2 |
|
|
|
||||||||
|
|
3 |
|
|
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
||||
Этот профиль показан на рис. 13 для q0 1.
59
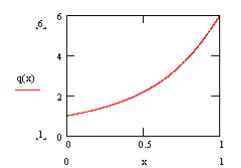
Рис. 13. Профиль q для q0 1. |
|
||||||
Найдем теперь форму силовых линий. |
|
||||||
Уравнения их в цилиндрической системе координат |
|
||||||
имеют вид: |
|
|
|
|
|
|
|
|
rd |
|
|
dz |
. |
(II.2.7) |
|
|
H |
|
|
||||
|
|
|
Hz |
|
|||
Решение этого уравнения имеет вид: |
|
||||||
0 |
|
H |
z − z0 . |
(II.2.8) |
|||
|
|
||||||
|
|
|
rHz |
|
|||
Очевидно, что силовые линии представляют
собой спирали, намотанных на цилиндрические поверхности. Такие поверхности называются магнитными поверхностями. Для описания тороидальной системы с малой тороидальностью
60
