Морозов Введение в теорию горячей плазмы Ч.1 2011

Это уравнение очень похоже на уравнение (VIII.1.2), описывающее пучок невзаимодействующих частиц.

Перейдем в систему отсчета, движущуюся со

скоростью v cs или v −cs; v′ v cs. Тогда вместо (VIII.2.8) имеем:

Теперь оно в точности совпадает с уравнением (VIII.1.2), описывающим поток невзаимодействующих частиц. Следовательно, на нелинейной стадии также должно происходить укручение фронта ионно-звуковой волны, переходящее в ударную волну при ∂∂vx → . На

фронте такой волны, как и на фронте всякой ударной волны, происходит диссипация механической энергии вследствие вязкости.

VIII.3. Нелинейные МГД-волны

Рассмотрим поперечную МГД-волну cos 0 , т.е. магнитный звук, в приближении 8H2P 1.

Уравнения, описывающие такую волну, имеют вид:

181

Из последних двух уравнений видно, что

Далее можно проделать все те же выкладки, что и для ионного звука. Следовательно, также должно наблюдаться укручение и "опрокидывание" фронта.

Что касается альфвеновской волны, для нее v k, поэтому v, v 0, и при больших может происходить распространение нелинейной альфвеновской волны без искажения. Однако при1 альфвеновская волна также опрокидывается из-за перекоса силовых линий.

VIII.4 Волны на мелкой воде

Рассмотрим еще один вид нелинейных волн, имеющих важное значение не только в физике плазмы, но и в геофизике – это волны на мелкой воде.

Пусть на твердую поверхность налит слой воды

182

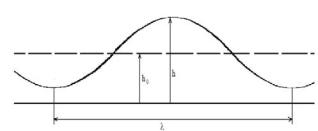
толщиной h0. Пусть также по этому слою воды распространяется одномерная волна в направлении x, причем длина волны много больше глубины слоя h0, h0 (см. рис.26)

Ввиду малой толщины слоя можно считать, что жидкость смещается только в направлениях x, а скорость этого смещения не зависит от высоты. Жидкость будем считать несжимаемой, const. Давление жидкости определяется гидростатическим законом:

Уравнения гидродинамики, описывающее такую волну, принимают вид:

Уравнение непрерывности теперь перепишется так:

Рис 26. Волна на мелкой воде

183

Будем считать, что высота слоя и скорость связаны однозначно: h h v . Тогда вместо уравнений (VIII.4.2) и (VIII.4.3) можно написать:

Умножая (VIII.4.5) на dhdv и вычитая из него

(VIII.4.4), получаем:

h ∂∂vx g dhdv 2 ∂∂vx ,

или

∂∂hv hg

и

Таким образом, и в этом случае получаем результат, аналогичный результату для ионного звука.

Полагая h h′ h0, где h′ h0, получаем:

184

cо всеми вытекающими из него следствиями. Заметим, что во всех рассмотренных случаях не

учитывалась дисперсия, т.е. ∂∂k const. Учет даже

слабой дисперсии приводит к важным физическим результатам.

VIII.5. Волны в средах со слабой дисперсией. Уравнение Кортевега-де Вриза. Солитоны

Учтем малую дисперсию при распространении ионного звука. В линейной задаче для этого типа волн был получен следующий закон дисперсии:

k2r2

2 2 De .

pi 1 k2r2De

При krDe 1 дисперсия отсутствовала:≈ pikrDe, и групповая скорость не зависела от k,

185

т.е. vqr pirDe mTei .

Однако учет следующего малого члена в разложении выражения (VIII.5.1) приводит к появлению дисперсии:

на которой изменение групповой скорости оказывается порядка ей самой.

Учтем малую дисперсию в нелинейном уравнении для простых волн. Для этого перейдем в

Выполняя обратное фурье-преобразование,

Но при конечной амплитуде возмущения

уравнение должно содержать член u ∂∂ux . Таким

образом, полное уравнение должно содержать и нелинейный член, и член, описывающий

186

Это уравнение носит название "Кортевега-де Вриза" и было получено в 1895 г.

Уравнение Кортевега-де Вриза допускает новый тип решений – уединенную волну (солитон).

Для того, чтобы найти такое решение, перейдем в систему отсчета, движущуюся с некоторой, пока неопределенной, скоростью c и введем новую

Здесь a – постоянная интегрирования. Прибавив к скорости u постоянную величину, можно добиться того, чтобы a обратилась в ноль.

Полученное уравнение в точности совпадает с уравнением, описывающим движение классической материальной точки в поле сил с потенциалом

187

Потенцитал представлен на рис.27.

Масса частицы при этом равна m

переменная соответствует времени, а переменная u – отклонению от точки положения равновесия. Точка u 2c соответствует положению равновесия, а малые колебания вблизи этого положения являются линейными:

Величина u0 здесь соответствует амплитуде колебаний, а решение (VIII.8.5) – периодической волне, распространяющейся со скоростью c. С ростом амплитуды колебания все более отличаются от гармонических. Если u0 достигает величины 3c, решение переходит в уединенную волну, показанную на рис. 28.

Решение при этом имеет вид:

Такое решение называется уединенной волной

(solitary wave), или солитоном.

188

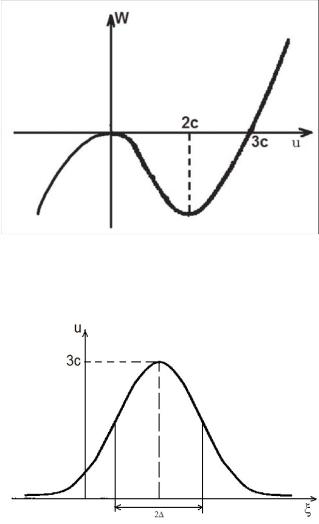
Рис. 27. Эффективный потенциал

Рис. 28. Солитон

Подставим решение (VIII.5.11) в уравнение

189

Выбрав амплитуду и параметр 2u0, можно найти ширину солитона.

В среде с отрицательной дисперсией групповая скорость vgr v0gr 1 − 2kk22 . Неопределенная ранее

0

скорость (в системе отсчета, двигающейся со скоростью c0) равна

т.е. солитон распространяется со скоростью больше скорости звука.

Полученные решения имеют интересные приложения в геофизике. С ними связывают иногда встречающиеся в океане одинокие "волны-убийцы", появляющиеся неожиданно и имеющие громадную высоту.

190