
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf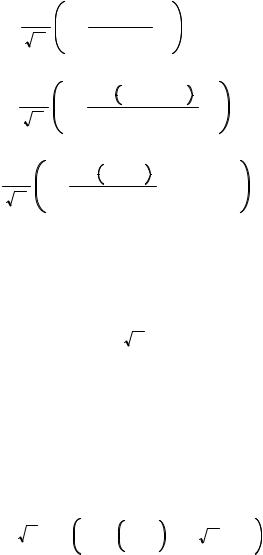
|
x |
|
|
exp −z2 |
|
|
|
|
|
|
|
z − x |
dz |
|
(IV.5.13) |
||
|
|
|
− |
|
|
VP |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
exp |
− u x 2 |
|
|
|
|
|
|
|
u |
|
du |
≈ |
|
|
|
|
− |
|
|
|
|
VP |
|
|
|
|
|
|
|
|
|
|
x |
|
exp − u 2 |
|
|
|
||
≈ |
|
|
u |
|
1 − 2ux du |
. |
||
|
|
− |
|
|
|
|
|
VP |
|
|
|
|
|
|
|
|
|
Здесь |
мы |
перешли |
к |
новой |
переменной |
|||
интегрирования u z − x. Первый член в скобках при интегрировании даёт ноль, и окончательно получаем:
F x −2x2 i |
x; x 1. |
(IV.5.14) |
Как мы уже видели, из уравнения div E 0
следует, что в однородной незамагниченной плазме для продольных электростатических волн дисперсионным уравнением является уравнение0. Очевидно, что затухание волны определяется мнимой частью . При x 1 она экспоненциально мала. В случае x 1
1 |
2 |
p |
1 − 2 |
|
2 |
i |
|
|
. |
(IV.5.15) |
|
kvT |
|
|
|||||||
|
|
kvT |
|
|
|
kvT |
|
|||
111

Здесь затухание пропорционально лишь первой
степени параметра |
p |
. Очевидно, что |
сильнее |
|||
kvT |
||||||
|
|
p |
|
|
||
всего волна затухает, |
когда |
1, т.е. |
в том |
|||
kvT |
||||||
случае, когда фазовая скорость волны совпадает с тепловой скоростью. Именно в этом месте максвелловская функция распределения имеет максимальную производную.
Заметим, что все предыдущие выводы сделаны в предположении ′ , а движение ионов не учитывалось.
IV.6. Учёт движения ионов
Для распространения волн с меньшими частотами, чем те, что исследовались в предыдущем разделе, необходимо учитывать движение ионов. При выводе возмущённой функции распределения вид частиц не конкретизировался, а в формулу (IV.3.4), из которой и получается дисперсионное уравнение, возмущённые плотности электронов и ионов входят аддитивно, можно не проводить вычислений для ионов, а просто добавить соответствующий член в выражение для (IV.5.10):
k, 1 |
4 nee2 |
1 F |
|
|
(IV.6.1) |
|
k2Te |
kvTe |
|||||
|
|
|
|
112

|
4 nie2 |
1 F |
|
. |
|
k2Ti |
kvTi |
||||
|
|
|
|||
Здесь индексы е и i относятся к электронам и |
|||||
ионам соответственно. Следует помнить также о квазинейтральности плазмы, ne ≈ ni. Заметим, что второй и третий член вошли с одинаковыми знаками, хотя возмущения плотности входят в уравнение (IV.3.4) с разными. Дело в том, что возмущения плотности электронов и ионов пропорциональны каждое своему заряду, т.е. имеют противоположные знаки.
Рассмотрим предельные случаи. Если ионная температура не слишком превосходит
электронную, то vTe |
vTi. Значит, если |
|
1, |
|||||
kvTe |
||||||||
|
|
|
|
|
|
|
||
то заведомо |
|
1, |
и такая волна на ионах не |
|||||
kvTi |
||||||||
затухает. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
Рассмотрим теперь случай |
|
|
||||||
|
|
|
|
|
|
|
||
|
|
vTi |
|
|
vTe, |
|
(IV.6.2) |
|
|
|
k |
|
|||||
т.е. фазовая скорость волны много больше ионной тепловой скорости, но много меньше электронной. Тогда в выражение (IV.6.1) можно
подставить разложение в ряд функции F |
|
|
и |
|
|
kvTe |
|||
ассимптотику вместо функции F |
|
|
|
|
|
. |
В |
||
kvTi |
||||
результате для получаем: |
|
|
|
|
113

|
|
1 − |
|
pi2 |
|
|
|
1 |
|
1 i |
|
. |
||||||
|
|
|
2 |
krDe |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
kvTe |
|||||
Здесь |
мы ввели |
|
|
ионную |
плазменную частоту |
|||||||||||||
pi |
|
4 nie2 |
(в |
|
|
отличие |
от |
электронной |
||||||||||
|
|
mi |
|
|
|
|
||||||||||||
плазменной pe |
|
|
4 nee2 |
). Напомним также, что |
||||||||||||||
|
|
|
me |
|
||||||||||||||
rDe,i |
|
|
|
Te,i |
. |
Пренебрежём |
мнимой частью в |
|||||||||||
|
|
2 |
||||||||||||||||
|
|
|
|
4 ne |
|
|
|
|
|
|
|
|
|
|
|
|||
(IV.6.3) и в коротковолновом пределе krD 1, находим действительную часть частоты:
2 k2 Te .
mi
Очевидно, что эта бесстолкновительная (!) волна имеет фазовую скорость, очень похожую на фазовую скорость обычного (столкновительного) звука. Поэтому этот тип волн называют ионным звуком. При этом в формулу входит электронная температура и ионная масса. Очевидно, что его фазовая скорость много меньше электронной тепловой, что соответствует предположению
(IV.6.2).
С другой стороны, фазовая скорость магнитного
звука должна быть много больше тепловой скорости ионов (см. (IV.6.1)). В противном случае волна будет сильно затухать на ионах.
(IV.6.3)
(IV.6.4)
114

|
vph |
Te |
|
Ti |
|
|
|
|
mi |
|
mi |
. |
|
(IV.6.5) |
|
Очевидно, что это неравенство может |
|||||||
выполняться только в случае |
|
|
|
|
|||
|
|
Te |
Ti. |
|
|
|
(IV.6.6) |
Таким |
образом, |
|
ионный |
звук |
может |
||
распространяться без сильного затухания только в |
|
|||||||||
плазме, для которой электронная температура |
|
|||||||||
существенно превышает ионную. Такой режим |
|
|||||||||
обычно осуществляется в плазме с редкими |
|
|||||||||
столкновениями, нагреваемой текущим по ней |
|
|||||||||
током, в частности, в токамаках с омическим |
|
|||||||||
нагревом. Декремент затухания ионного звука |
|
|||||||||
получим из (IV.6.3). В первом по |
|
|
приближении |
|
||||||
|
|
|
|
|||||||
находим: |
|
|
|
|
|
kvTe |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
2 |
|
|
|
|
||
|
|
pik |
|
rDe 1 − i |
|
|
. |
(IV.6.7) |
||
|
|
kvTe |
||||||||
Подставим сюда ′ i и отделим мнимую часть от действительной. При этом можно значение′ подставить из нулевого приближения. В результате находим :
− pikrDe |
me |
. |
(IV.6.8) |
|
|||
|
8mi |
|
|
Рассмотрим теперь |
длинноволновый |
предел |
|
115

1/rDe k 1/rDi. Легко видеть, |
что это условие |
может быть выполнено только при Te Ti. В этом |
|
случае приравнивая нулю, из (IV.6.3) получаем в |
|
нулевом приближении: |
|
2 pi2 . |
(IV.6.9) |
Затухание на электронах экспоненциально мало
и определяется только ионами. Из (IV.6.7) в этом пределе находим:
|
− |
|
|
pi2 |
|
− |
|
pi2 |
1 |
. |
(IV.6.10) |
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
k2rDevTe |
2 2 pe krDe |
|
|||||||
Очевидно, |
что условие |
слабого |
затухания |
|||||||||
/ pi |
1 |
может |
выполняться |
только |
при |
|||||||
krDe |
me/mi . |
|
|
|
|
|
|
|
|
|||
IV.7. Квазилинейная теория затухания Ландау
Линейное приближение позволяет установить сам факт неустойчивости и проследить ее развитие лишь на самой начальной стадии. Для того, чтобы понять, к чему развитие неустойчивости приведёт, надо учитывать следующие члены разложения в кинетическом уравнении. В большинстве случаев это удаётся сделать лишь численно. Однако, если возмущения остаются малыми и на нелинейной
116
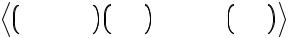
стадии (т.н. слабая турбулентность), существуют аналитические методы исследования. Это так называемая квазилинейная теория. Аналогичная задача возникает и при затухании слабой волны на нелинейной стадии.
При линейном анализе мы предполагали, что
функция распределения представляет собой сумму
f0 f, где f0 не зависит от времени. В квазилинейном приближении мы будем предполагать, что f0 сама медленно меняется под действием возмущения. Предположим также, что в плазме существуют быстрые мелкомасштабные осцилляции, характерные периоды которых существенно меньше характерного времени и масштаба изменения функции f0. Волной над буквой мы будем обозначать быстропеременные функции, а угловыми скобками − усреднение по отрезку времени , превосходящему периоды быстрых осцилляций, но много меньшему характерного времени изменения f0, и по отрезку L, превосходящему длину волны осцилляций. Кинетическое уравнение запишется тогда так:
∂ |
|
∂ |
|
|
∂ |
|
|
|
|
v |
f0 f |
e E |
f0 f |
0. |
(IV.7.1) |
||||
∂t |
∂x |
∂p |
|||||||
|
|
|
|
|
|
При усреднении члены, содержащие нечётные
степени быстро осциллирующих функций, обратятся в ноль. Поэтому усреднённое уравнение приобретает вид:
117

∂ |
|
∂ |
|
∂ |
|
|
|
v |
f0 e E |
f . |
(IV.7.2) |
||||
∂t |
∂x |
∂p |
|||||
|
|
|
|
Так как возмущение функции распределения мы считаем малым, то положим, что оно связано с электрическим полем так же, как и в линейном приближении. Для фурье-образа это соотношение (IV.3.3). Используя это, вычислим квадратичный по возмущениям член в уравнении (IV.7.2).
|
∂ |
|
|
|
|
ie |
dt dkd Ek, exp −i t |
|
|
|
||||
E |
f |
− |
ikx |
(IV.7.3) |
||||||||||
|
∂p |
|
|
L |
||||||||||
|
|
|
′ |
|
′ |
∂ |
|
Ek′ ′ exp −i ′t ik′x |
∂f0 |
|
||||
|
dk |
d |
|
|
|
|
|
|
|
|
. |
|
||
|
|
|
∂p |
′ − k′v i |
∂p |
|
||||||||
При достаточно больших и L можно |
|
|||||||||||||
приближённо считать, что: |
|
|
|
|||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp −i ′ t i k k′ x dtdx L, |
(IV.7.4) |
||||||||||||
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
если ′ 0; k k′ 0.
В других случаях этот интеграл равен нулю. Таким образом, усреднённое произведение (IV.7.3) сводится к следующему:
|
∂ |
|
−ie dkd |
∂ |
|
Ek, E−k,− ∂f0 |
|
||
E |
|
f |
|
|
|
|
|
. (IV.7.5) |
|
∂p |
∂p |
kv − i |
∂p |
||||||
118

Так как электрическое поле является действительной величиной, должно выполняться
соотношение |
E−k,− Ek, , |
и |
кинетическое |
|||||||||||
уравнение принимает вид: |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
∂ |
v |
|
|
∂ |
|
f0 |
|
|
|
(IV.7.6) |
|
|
|
|
∂t |
|
∂x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
−ie2 |
∂ |
dkd |
|
|
|
|E|k2, |
|
|
∂f0 |
|||||
|
|
|
|
|
. |
|||||||||
∂p |
|
|
kv − i |
∂p |
||||||||||
Снова воспользуемся соотношением (IV.4.2) и проинтегрируем по , а также будем считать, что f0 не зависит от x. Кроме того, в практически
интересных случаях спектр можно считать симметричным относительно точки kv , т.е. |E|2k, - чётная функция от − kv. В этом случае
интеграл в смысле главного значения выпадает. В результате имеем:
∂f0 |
e2 |
∂ |
dk|E|2 |
kv |
∂f0 |
. |
(IV.7.7) |
∂t |
∂p |
|
|||||
|
|
|
∂p |
|
|||
Для того, чтобы вычислить обе неизвестные функции, f0 и |E|2, необходимо иметь второе
уравнение.
В линейном приближении |
|
Ek, Ek, exp −i t t ikx . |
(IV.7.8) |
Здесь под мы понимаем действительную часть
119
частоты. Комплексно сопряжённое значение этой функции имеет вид:
Ek, Ek, exp i t t − ikx , |
(IV.7.9) |
откуда получаем: |
|
EE Ek, Ek, exp 2 t , |
|
т.е. |
|
|
d |
|
|E|2 2 |E|2. |
|
|
||||
|
dt |
|
|
||||||
|
|
|
|
|
|
|
|||
Величину можно подставить из линейного |
|||||||||
приближения, |
|
|
|
|
|
|
|
||
|
|
4 2e2 peme ∂f0 |
, |
(IV.7.10) |
|||||
|
|
k2 |
|
|
∂p |
||||
|
|
|
|
|
|
|
|
||
где под f0 |
следует |
понимать |
медленно |
||||||
меняющуюся со временем искомую функцию. Таким образом, уравнения (IV.7.7) и
(IV.7.10) составляют полную систему уравнений для исследования эволюции волны и функции распределения электронов при распространении волны в бесстолкновительной плазме. Пример эволюции функции f0 приведён на рис. 22.
120
