Морозов Введение в теорию горячей плазмы Ч.1 2011

u0 u3 us – ослабляется.

VII.3. Ударные волны в слабых полях

Рассмотрим случай, когда давление плазмы много больше магнитного

В остальном скачки всех величин считаем произвольными. В уравнении адиабаты пренебрежем в первом приближении членом, связанным с магнитным полем

171

Эти соотношения такие же, как в обычной газодинамике. Найдем скачок тангенциальной составляющей поля. Выражая vt из (VI.2.14) и подставляя в (VI.2.13), получаем:

Правая часть (VII.6.4) квадратична п о Hn, и ею можно пренебречь, т.е.

Уравнения (VI.2.1 − 1 14) представляют и другую возможность: скачок плотности мал, а поток вещества через фронт – малая величина второго порядка

С другой стороны, при 1 ≈ 2 ударная адиабата превращается в том же приближении в

172

уравнение

Условие 2 2 – это условие несжимаемости, т.е. уравнение (VII.6.9) - это ударная адиабата для несжимаемой жидкости. Тангенциальная составляющая магнитного поля не изменяется по направлению, но совершает скачок по величине. Скорость распространения разрыва, иначе фронта волны определяется так:

то есть равна альфвеновской скорости, вычисленной по нормальной составляющей поля. Так как в такой волне P2 P1, ослабляется тангенциальная составляющая магнитного поля:

Рассмотрим теперь два частных случая волн произвольной магнитуды в произвольных полях.

Пусть перед фронтом волны магнитное поле перпендикулярно фронту, Ht1 0 . Тогда уравнение (VII.6.4) переходит в следующее:

Пусть Ht2 ≠ 0 и произвольно. Тогда

173

распространение волны поперек поля, Hn 0. Для этого случая u2 u3. Имеется только один тип волн.

Из уравнения

Выбором системы координат можно добиться vt 0. В этой системе вещество течет перпендикулярно фронту. Тогда из уравнения

(VII.6.4) находим:

174

написать:

что и является ударной адиабатой для перпендикулярной волны.

VII.4. Генерация магнитного поля при турбулентном движении

Многие астрофизические объекты, такие, как галактика, звезды, планеты, межзвездные облака, обладают собственными магнитными полями. Образование этих полей в настоящее время связывают с самопроизвольной генерацией магнитного поля при турбулентном движении проводящей жидкости. Такая генерация наблюдается и в экспериментальных установках, в частности, в пинчах с обращенным полем.

В проводящей жидкости всегда существуют спонтанные поля, не связанные с движением жидкости. Покажем, что в зависимости от свойств этой жидкости (в частности, плазмы) такие поля могут либо затухать, либо усиливаться. С одной стороны, магнитные поля затухают за счет омической диссипации. С другой стороны, магнитное поле в силу вмороженности может нарастать из-за "растяжения" в среднем линий тока жидкости и, соответственно, силовых линий поля.

Пусть вначале магнитное поле достаточно

175

слабое и не влияет на движение жидкости. Для простоты будем считать жидкость несжимаемой,const, divv 0. Движение тогда описывается уравнением Навье Стокса:

Если величина v задана, то оно полностью описывает эволюцию магнитного поля.

Функции и H удовлетворяют одному и тому же уравнению, если 4c2 . В этом случае может существовать решение

При стационарной (в среднем) турбулентности стационарно (в среднем) и магнитное поле H, т.е. в

176

среднем генерация и затухание уравновешены. Если4c2 , диссипативные потери будут меньше, чем

возрастание (в среднем) магнитного поля за счет растяжения силовых линий, и будет наблюдаться спонтанная генерация магнитного поля.

Эта аргументация не применима для двумерной турбулентности, например, в токамаках.

Условие генерации может выполняться в звездных атмосферах и межпланетной плазме.

Глава VIII. Нелинейные волны в плазм

VIII.1. Простые волны

В предыдущем разделе мы уже рассмотрели ряд нелинейных явлений в плазме, в частности, распространение разрывных решений. Однако структура разрывов при этом не рассматривалась. В настоящей главе мы более подробно рассмотрим нелинейные явления в плазме.

Для начала рассмотрим простейшую модель: пусть вдоль оси x движется неограниченный в пространстве пучок невзаимодействующих частиц с одинаковыми скоростями v. Уравнение, описывающее такой поток, имеет вид:

177

Очевидно, что частицы, для которых u 0, будут догонять более медленные, движущиеся вправо. Вблизи точек, для которых sin kx 0, частицы будут скапливаться. Аналогичная картина будет и для частиц, у которых u 0. В результате профиль волн будет становиться все круче, а точки kx l l 0, 1, 2. . . будут точками сгущения плотности (см. рис.25). В дальнейшем это приводит к "опрокидыванию фронта".

Это называется "бунчировкой" частиц.

При изменении формы волны возникают высшие гармоники ряда Фурье. В нулевом приближении u 0 sin kx. Считая квадратичные члены малыми, в первом приближении получаем:

становится масштаба нулевой, и метод теории возмущения перестает быть применимым.

178

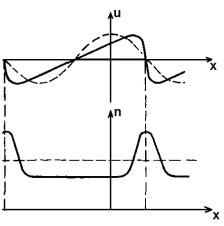
Рис.25. Укручение фронта волны

VIII.2. Нелинейное распространение ионного звука

Рассмотрим теперь нелинейное распространение ионного звука. Для простоты будем считать Ti 0, а электронную теплопроводность устремим к бесконечности, т.е. положим Te const. Тогда в отсутствие магнитного поля уравнения, описывающие плазму, принимают вид:

179

уравнения (VIII.2.1) и (VIII.2.2) перепишем так:

Подставляем это выражение в последний член уравнения (VIII.2.4):

180