
Морозов Введение в теорию горячей плазмы Ч.1 2011
.pdf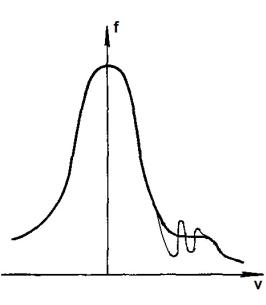
Рис. 22. Эволюция функции распределения электронов при распространении волны в бесстолкновительной плазме
Из рисунка видно, что функция, которая была первоначально максвелловской, начинает уплощаться в точке, соответствующей скорости частиц, равной фазовой скорости волны, образуя постепенно "столик" вблизи этой точки. Конечно, редкие столкновения, которые мы здесь не учитывали, постепенно разрушают столик, а волна затухает до нуля.
121
Глава V. Уравнения магнитной гидродинамики. Метод моментов
Сплошные среды часто описываются уравнениями гидродинамики (см. напр. [10])
Уравнения эти обычно получаются из рассмотрения баланса сил, действующих на единичный объём жидкости. Тем же способом можно описывать и газы в том случае, когда длина свободного пробега частиц много меньше характерного размера задачи. В случае замагниченной плазмы пределом применимости является условие малости ларморовского радиуса по сравнению с характерным размером (подробнее об этом см. [11]). Однако при этом остаётся открытым вопрос: как связана гидродинамика с кинетикой и можно ли получить из кинетики предельным переходом уравнения гидродинамики. Мы попытаемся ответить на этот вопрос в настоящем разделе. Для этого рассмотрим метод моментов.
Моментом функции распределения с номером n являются интегралы вида
Mn v nfdp. |
(V.0) |
122
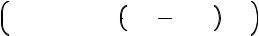
Для того, чтобы получать уравнения для
моментов, будем умножать кинетическое уравнение на соответствующую степень скорости и интегрировать по импульсному пространству.
V.1. Нулевой момент (уравнение непрерывности)
Для того, чтобы получить нулевой момент, просто проинтегрируем кинетическое уравнение по пространству импульсов.
dp |
∂f |
v f Ze |
E |
1 |
v, H |
∂f |
(V.1.1) |
dt |
c |
dp |
Stdp.
Впервом члене можно поменять порядок
интегрирования и дифференцирования. По определению fdp n, где n − плотность. Тогда
имеем: |
|
|
|
|
|
|
|
dp |
∂f |
∂n |
|
||
|
|
|
|
. |
(V.1.2) |
|
|
dt |
∂t |
||||
Во втором члене также меняем порядок |
||||||
интегрирования |
и |
дифференцирования. |
По |
|||
123
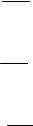
определению dpvf nV, где V − средняя скорость. Таким образом,
dp v f divnV. |
(V.1.3) |
Член, пропорциональный электрическому полю,
обращается в ноль. Действительно, в компонентах его можно переписать так:
Ze E |
∂f |
dpxdpydpz |
(V.1.4) |
|
∂p |
||||
|
|
|
Ze 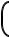 Ex ∂∂pfx dpx
Ex ∂∂pfx dpx  dpydpz
dpydpz
Ze  Ey ∂∂pfy dpy
Ey ∂∂pfy dpy  dpxdpz
dpxdpz
Ze 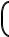 Ez ∂∂pfz dpz
Ez ∂∂pfz dpz  dpydpx
dpydpx
Так как функция распределения обращается в ноль при бесконечных импульсах, каждый из этих интегралов обращается в ноль.
Член, пропорциональный магнитному полю, также обращается в ноль (см. задачу к этому разделу).
Интеграл от столкновительного члена также должен обращаться в ноль, т.к. если мы не учитываем процессов рождения-поглощения частиц, он не должен менять число частиц.
124
Покажем это. Мы будем учитывать только парные столкновения. Мгновенный уход частиц из объёма фазового пространства вблизи импульса p происходит вследствие столкновения с другой частицей с произвольным импульсом p′. Скорость ухода пропорциональна фазовой плотности таких частиц (т.е функции распределения f , где индекс означает сорт частицы) и вероятности w p, p′, p′′ того, что частица после столкновения будет иметь импульс p′′. Очевидно, что импульс второй частицы после столкновения однозначно определяется законом сохранения импульса. В результате столкновений частицы не только уходят из данного фазового объёма, но и приходят в него. Если частица пришла в него в результате столкновения частиц с импульсами p′ и p′′, то скорость прихода
пропорциональна обеим фазовым плотностям и вероятности w p′, p′′, p . В результате столкновительный член, определяемый балансом прихода и ухода частиц, принимает вид:
St ∑ dp′dp′′f p′ f p′′ w p′, p′′, p − |
(V.1.5) |
|
|
− f p f p′ w p, p′, p′′ .
Так как частица сталкивается с частицами всех
сортов, присутствующих в плазме и имеющих всевозможные импульсы, здесь проведено суммирование по всем сортам частиц и интегрирование по p′ и p′′. Проинтегрируем это
125
соотношение по dp и переобозначим в первом члене
немые переменные p′ → p, p′′→ p′. |
После такого |
переобозначения этот член просто совпадает со |
|
вторым. Таким образом, |
|
Stdp 0, |
(V.1.6) |
что и требовалось доказать. Следовательно,
уравнение для первого момента является уравнением непрерывности
∂n |
divnV 0. |
(V.1.7) |
|
∂t |
|||
|
|
Если в плазме имеют место процессы ионизации и рекомбинации, в правую часть должны быть добавлены члены, описывающие рождение и поглощение частиц.
Мы видим, что уравнение (V.1.7) содержит скорость, для определения которой требуется написать уравнение для следующего момента.
Задача
Доказать, что
|
v, H |
∂f |
dp 0. |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
∂p |
|
|
|
|
|
|
||
Решение |
|
|
|
|
|
|
|
|
|
|
Скалярное произведение |
под |
интегралом |
||||||||
содержит |
только члены вида viHj |
∂f |
, |
где |
все |
|||||
∂xk |
||||||||||
|
|
|
|
|
|
vxHy |
∂f |
|
||
индексы не равны друг другу, |
например, |
. |
||||||||
|
||||||||||
Интегрируя |
это выражение |
сначала |
по |
|
∂z |
|||||
dpz, а |
||||||||||
126

потом по dpx и dpy, видим, что первый интеграл − это интеграл от производной по pz, который равен разности f на бесконечных пределах, т.е. нулю. Аналогичным образом обращаются в ноль и интегралы от других членов.
V.2. Первый момент (аналог уравнения Навье-Стокса)
Умножим кинетическое уравнение почленно на i − компоненту скорости и проинтегрируем по импульсу
dpvi 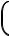 ∂dtf v f Ze
∂dtf v f Ze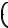 E 1c v, H
E 1c v, H  d∂pf
d∂pf 
viStdp.
Меняя в первом члене порядок интегрирования
и дифференцирования, легко получаем:
vi ∂dtf dp ∂∂t nVi.
Поступая таким же образом со вторым членом,
получаем:
vivj |
∂f |
dp |
∂ |
n vivj . |
|
|
|||
|
dxj |
∂xj |
||
(V.2.1)
(V.2.2)
(V.2.3)
127

К вычислению этого среднего мы вернёмся
позже.
Член, пропорциональный электрическому полю, содержит множитель
vi |
∂f |
dp dp dp |
1 |
pi |
∂f |
dp dp dp . |
(V.2.4) |
∂pj |
m |
∂pj |
Рассмотрим сначала случай, когда i не равно j.
Снова интегрируем сначала по pj и видим, что этот интеграл обращается в ноль.
Рассмотрим теперь случай i j. Интегралы типа
pi ∂∂pfi dp dp dp берём по частям, например,
px |
∂f |
dpxdpydpz |
(V.2.5) |
|
|||
|
∂px |
|
|
pxf dp dp − fdp dp dp .
−
Первый интеграл в (V.2.5) равен нулю, а второй
есть не что иное, как плотность. Таким образом, имеем:
vi |
∂f |
|
|
|
ij |
|
|
||
|
dp dp dp |
− |
m |
n, |
(V.2.6) |
||||
∂pj |
|||||||||
и, соответственно, |
|
|
|
|
|
|
|||
ZeEj vi |
∂f |
dp − |
Zen |
Ei. |
(V.2.7) |
||||
∂pj |
|
m |
|||||||
128

Здесь ij символ Кронекера.
Аналогичным образом можно показать, что |
|
||||||
Ze |
v |
v, H |
∂f |
dp |
Zen |
V, H . |
(V.2.8) |
c |
∂p |
c |
|||||
Вернёмся теперь ко второму члену, включающему среднее vivj . Чтобы вычислить это среднее, разобьём скорость частицы на две составляющие, одна из котрых, V, совпадает со средней упорядоченной скоростью плазмы, а другая, u − хаотическая скорость, среднее от которой равно нулю.
vi Vi ui; vivj Vi ui Vj uj |
(V.2.9) |
Члены, содержащие нечётные степени u, выпадают, т.е.
vivj ViVj uiuj |
(V.2.10) |
Исследуем теперь тензор uiuj ≡ ij, который
называют тензором напряжений. Если функция распределения изотропна в системе координат, движущейся вместе с потоком, то он становится диагональным. Для максвелловской функции распределения
2 |
|
T |
2 |
|
T |
|
∑ uiuj 3 ui |
3 |
m |
; ui |
|
m |
(V.2.11) |
i
в том случае, если температура частиц, движущихся параллельно, равна температуре
129
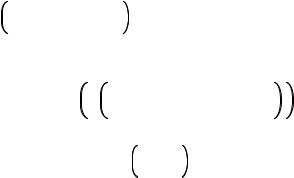
частиц, движущихся в перпендикулярном направлении. Однако в плазме эти температуры бывают разными. Тогда приходится вводить для них T и Т . Таким образом, второй член в уравнении (V.2.1) принимает вид:
∂ |
n uiuj nVj |
∂ |
Vi Vi |
∂ |
nVj |
∂ |
nT. |
(V.2.12) |
|
|
|
|
|||||
∂xj |
∂xj |
∂xj |
∂xi |
|
||||
Произведение nT равно давлению данного сорта
частиц P (соответственно, P и P для разных температур), а второй член в правой части (V.2.12) можно выразить из уравнения непрерывности так:
Vi |
∂ |
nVj |
−Vi |
∂n |
. |
(V.2.13) |
∂xj |
|
|||||
|
|
|
∂t |
|
||
Недиагональные компоненты тензора ij описывают вязкость плазмы. В незамагниченной плазме соответствующий член
2 |
∂ |
|
n uiuj − |
u′ 2 |
|
|
ij |
≡ |
|
∂ |
ij |
имеет |
вид |
(см. |
||||||||||||
∂xj |
3 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xj |
|
|
|
|
|
|
|
||||||
напр. [13]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∂ |
n uiuj |
|
|
∂ |
|
|
|
|
∂Vi |
|
|
∂Vj |
− |
2 ∂Vl |
ij |
(V.2.14) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∂xj |
|
∂xj |
|
|
|
∂xj |
|
∂xi |
3 ∂xl |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
∂Vl |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
∂xi |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂xl |
|
|
|
|
|
|
|
|||||||
|
Здесь |
|
|
и |
|
− коэффициенты |
вязкости. |
|||||||||||||||||||
Напомним, что подразумевается суммирование по
130
