Физика [РТФ, Браже & Долгов, 1 семестр] / Шизика

Таким образом,

Поток вектора индукции электрического поля через произвольную замкнутую поверхность равен заряду, охватываемому этой поверхностью.

Выражение (4.9), представляющее собой математическую за-

пись третьего уравнения Максвелла, называют также теоремой

Гаусса – Остроградского.

§ 5. Четвертое уравнение Максвелла

Теорема Гаусса – Остроградского (4.9) показывает, что элек-

трическое поле создается электрическими зарядами. Так как маг-

нитное поле, согласно (4.6), создается токами проводимости (движущимися электрическими зарядами) и токами смещения (изменяющимися во времени электрическими полями), то отдельных магнитных зарядов нет. Поэтому

Поток вектора индукции магнитного поля через произвольную замкнутую поверхность равен нулю:

Это утверждение составляет содержание четвертого уравнения Максвелла.

§ 6. Полная система уравнений Максвелла

Сведем теперь выражения (4.4), (6.6), (4.9), (4.10) в единую систему уравнений, называемых уравнениями Максвелла в честь этого создателя теории электромагнитного поля (первые уравнения такого поля были им записаны в 1855–1856 гг.):

72

S

Уравнения Максвелла обычно дополняют тремя уравнениями, связывающими входящие в них векторные функции коэффициентами, зависящими от свойств среды:

С первыми двумя уравнениями мы уже знакомы: это связь индукции и напряженности электрического и магнитного полей. Третье выражение представляет собой закон Ома в дифференциальной форме. Здесь σ – удельная электропроводность среды (величина, обратная ее удельному электрическому сопротивлению). Действительно, в однородном электрическом поле отрезка прямого провода напряженность поля E =U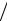I , где U – падение напряжения на участке длиной l, сила тока, согласно (4.12),

где R – сопротивление провода. Полученное выражение представляет собой обычную, интегральную форму записи закона Ома для однородного участка цепи.

73

Лекция 5

2.2. Электростатика и магнитостатика

§ 1. Уравнения электростатики и магнитостатики

Электростатикой называется часть теории электричества, занимающаяся изучением электрических полей неподвижных электрических зарядов.

Магнитостатикой называется часть теории магнетизма, занимающаяся изучением магнитных полей постоянных электрических токов.

В обоих случаях мы имеем дело со стационарной ситуацией, когда состояние источников полей и сами поля не зависят от времени. В этом случае система уравнений Максвелла (4.11) с учетом уравнений связи (4.12) распадается на две независимые системы уравнений:

− уравнения электростатики

∫ DdS = ∫ρdV ,

74

К этим уравнениям следует добавить выражения, определяющие характеристики модельных источников полей. К уравнениям (5.1) –

вытекающее из закона Кулона выражение для электрического поля точечного заряда:

а к уравнениям (5.2) – закон Био – Савара – Лапласа для магнитного поля элемента тока:

Данное уравнение аналогично по своему смыслу (5.3). Из него следует, что индукция магнитного поля, создаваемого элементом тока, как и напряженность электрического поля точечного заряда, обратно пропорциональна квадрату расстояния до него. Правда, вектор индукции магнитного поля является аксиальным вектором в отличие от вектора напряженности электрического поля, который является полярным вектором.

Кроме того, к уравнениям электростатики (5.1), (3.3) следует добавить условие безвихревого (потенциального) характера электростатического поля:

где скалярная функция ϕ является потенциалом электростатического поля, введенным в прошлой лекции. Здесь gradϕ − градиент потенциала, обозначающий его векторную производную следующего вида:

gradϕ = i ∂∂ϕx + j ∂∂ϕy + k ∂∂ϕz .

75

Формула (5.5) выражает тот факт, что разность потенциалов ка- ких-либо двух точек в электростатическом поле равна работе кулоновских сил по перемещению единичного положительного заряда из одной точки в другую:

Знак «минус» в (5.5) показывает, что с увеличением расстояния до заряда его электрическое поле ослабевает.

§ 2. Электроемкость. Конденсаторы

Электроемкостью проводника называется физическая ве-

личина, равная отношению накопленного на нем заряда к потенциалу электрического поля на его поверхности:

C = Qϕ .

Если рядом с заряженным проводником находится другой проводник, то на нем индуцируется заряд противоположного знака, а между проводниками возникает разность потенциалов ∆ϕ . Электрическое поле в такой системе проводников локализуется, в основном, между проводниками, а ее электроемкость выше, чем электроемкость уединенного проводника. Системы из двух разноименно заряженных проводников называются конденсаторами. Они служат для накопления электрического заряда и его передачи в другие участки электрической цепи. Емкость конденсатора находится по формуле

76

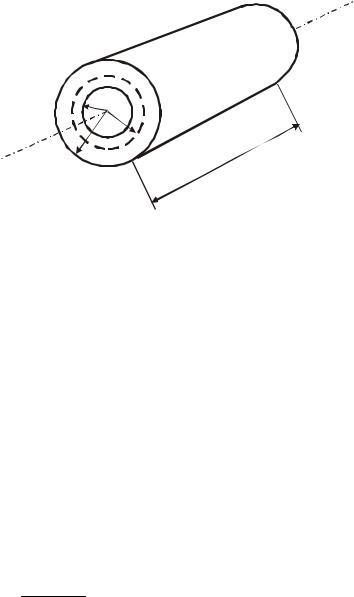
Рассмотрим в качестве примера цилиндрический конденсатор длиной l с радиусами проводников (обкладок) R1 и R2 > R1 , заполненный однородным изотропным диэлектриком с относительной диэлек-

∫DndS = Q.

S

Интегрирование в этом выражении проводится только по боковой поверхности цилиндра текущего радиуса R1 ≤ r ≤ R2 , так как через торцевые поверхности потоки вектора индукции электрического поля равны нулю. Поэтому, с учетом того, что Dn = D = ε0εE , данное выражение сводится к виду ε0εE 2πrl = Q , откуда напряженность электрического поля в конденсаторе

E = Q . 2πε0εrl

В аксиально-симметричном электростатическом поле связь напряженности и потенциала (5.5) принимает вид E = −dϕdr , следовательно, разность потенциалов между обкладками цилиндрического конденсатора

77

Подставляя полученное выражение в формулу (5.7), находим емкость цилиндрического конденсатора

В радиотехнике часто используется понятие погонной емкости, т. е. емкости, приходящейся на единицу длины линии передачи. Для коаксиального кабеля из формулы (5.8) получается следующее выражение для погонной емкости:

§ 3. Индуктивность. Соленоиды

Индуктивностью проводника называется физическая ве-

личина, равная отношению сцепленного с ним магнитного потока к силе протекающего в нем электрического тока:

L = ΦI .

Потокосцепление проводника с собственным магнитным полем будет больше, если он образует замкнутый контур, пронизываемый этим магнитным полем. Еще больше будет величина потокосцепления многовиткового контура – катушки индуктивности. Однослойную катушку индуктивности с плотно, виток к витку, намотанным

78

изолированным проводом называют соленоидом. Индуктивность соленоида можно вычислить по формуле

где Ψ = NΦ – потокосцепление соленоида из N витков с его собственным магнитным полем, созданным в результате протекания по нему тока силой I.

где n = Nl – число витков на единицу длины соленоида. Интеграл в левой части уравнения равен H 2πR . Следовательно, напряженность магнитного поля в соленоиде

Потокосцепление соленоида Ψ = ΦN = BS nl = µ0µIn2V , где V – внутренний объем соленоида. Подставляя последнее выражение в (5.10), найдем индуктивность тороидального соленоида:

79

Отметим, что формулы (5.11)–(5.13) справедливы также для прямого бесконечно длинного соленоида.

Выше предполагалось, что среда внутри соленоида (его сердечник) является однородным изотропным магнетиком, магнитная проницаемость которого постоянна и не зависит от силы тока, протекающего через соленоид. В некоторых случаях, например, при использовании ферромагнитных сердечников, магнитная проницаемость, а значит и индуктивность, зависят от величины магнитного поля, т. е. являются функцией силы тока в соленоиде.

§ 4. Энергия и силы в электростатике

Как было показано в школьном курсе физики, энергия заряженного конденсатора (пусть, для простоты, это будет плоский конденсатор емкости С, находящийся под напряжением U )

где S и d – соответственно площадь обкладок конденсатора и расстояние между ними, смысл остальных величин ясен из контекста. Поделив последнее выражение на объем конденсатора V, найдем объемную плотность энергии электрического поля в конденсаторе:

80