Физика [РТФ, Браже & Долгов, 1 семестр] / Шизика

Тангенс начальной фазы результирующих колебаний также легко определить из рис. 8.1, суммируя соответствующие проекции векторов:

рующих колебаний может принимать значения в интервале

A2 − A1 ≤ A ≤ A2 + A1.

Максимальное значение амплитуды Amax = A2 + A1 достигается при ∆ϕ = 2mπ , где m = 0,1,2,3,… Такие колебания называются синфазными. Синфазные колебания максимально усиливают друг друга. Минимальное значение амплитуды Amin = A2 − A1 становится возможным при ∆ϕ = (2m +1)π . Такие колебания называются противофазными. Противофазные колебания максимально ослабляют друг друга. При равенстве амплитуд складываемых противофазных колебаний наблюдается их полное взаимное гашение.

§ 2. Биения

Под биениями понимают результат наложения колебаний одинакового направления с близкими значениями частоты.

Пусть складываемые колебания описываются уравнениями

101

где ω2 =ω1 + ∆ω , причем ∆ω ω1 . Амплитуды обоих колебаний для простоты анализа приняты одинаковыми, а значения начальных фаз – нулевыми. Результат суммирования (8.6), (7.7) имеет вид

перепишем (8.8) в следующем виде:

Уравнение (8.10) описывает амплитудно-модулированные колебания, при этом амплитуда модуляции

График таких колебаний показан на рис. 8.2.

ψ Tb

2A

2A

t

T мод

Рис. 8.2. Картина биений в случае наложения колебаний одинаковой амплитуды

102

Рассмотренный случай представляет собой простейший пример модуляции амплитуды высокочастотных колебаний более низкочастотными гармоническими колебаниями. В представляющих интерес для практического использования в радиотехнике, телекоммуникационных системах и т. п. используются более сложные законы модуляции. При этом может модулироваться не только амплитуда, но также и частота, и фаза колебаний. Заметим, что периодические биения возникают только при наложений колебаний вида (8.6), (7.7). Как видно из рис. 8.2, период биений равен половине периода модуляции:

b 2 ∆ω

§ 3. Сложение взаимно перпендикулярных колебаний

Рассмотрим прямоугольную рамку, в центре которой находится шарик массой m, удерживаемый четырьмя одинаковыми пружинами жесткостью k (рис. 8.3).

Рис. 8.3. К сложению взаимно перпендикулярных колебаний

103

Такой шарик может совершать механические колебания как в горизонтальном (x), так и в вертикальном (y) направлении с частотой ω0 = k / m. Пусть уравнения этих колебаний имеют вид

т. е. начальные фазы колебаний подобраны таким образом, что их разность равна начальной фазе вторых колебаний.

Из уравнения (8.13) можем найти

Из уравнения (8.14) с учетом (8.15) получаем

Последнее выражение легко привести к виду

Проанализируем возникающие здесь частные случаи.

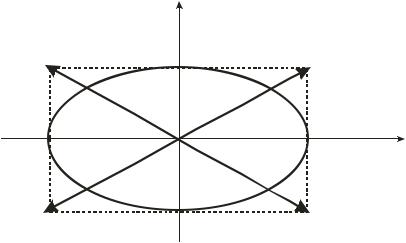
1. ∆ϕ = 0. В этом случае (8.16) сводится к уравнению прямой, проходящей через I и III квадранты (см. рис. 8.4):

104

x

Рис. 8.4. Результат сложения взаимно перпендикулярных колебаний

одинаковой частоты

2. ∆ϕ = ±π. Теперь из (8.16) получается уравнение прямой, проходящей через II и IV квадранты:

3. ∆ϕ = ±π / 2. При такой разности фаз складываемых колебаний (14.16) дает уравнение эллипса, приведенного к координатным осям:

На рис. 8.4 представлены все рассмотренные выше частные случаи движения шарика, участвующего в двух взаимно перпендикулярных колебаниях одинаковой частоты. В общем случае, если

105

∆ϕ ≠ 0, ±π ±,π шарик будет двигаться по эллипсу, уравнение которого задается формулой (8.16) для конкретного значения ∆ϕ . Направление вращения (по часовой стрелке или против часовой стрелки) определяется начальными условиями задачи.

§ 4. Фигуры Лиссажу

Французский ученый Ж. А. Лиссажу исследовал сложение взаимно перпендикулярных колебаний, отношения частот которых являются рациональными числами, т. е. ω1 / ω2 = p / q , где p и q – целые числа. Иначе говоря, вместо (8.13), (8.14) складываются взаимно перпендикулярные колебания следующего вида:

Не вдаваясь в детали, отметим, что при ∆ϕ =π / 2 в этом случае получаются замкнутые периодические движения с периодом T0 , равным наименьшему кратному из периодов T1 = 2π / ( pω) и T2 = 2π / (qω) складываемых колебаний. На рис. 8.5 показаны некоторые из таких кривых, называемых фигурами Лиссажу. При их п о- строении придерживаются следующего правила: отношение частот складываемых колебаний обратно отношению чисел пересечений кривой с осями координат, т. е.

p = Ny . q Nx

106

x

A2

в

Рис. 8.5. Примеры фигур Лиссажу

Для случаев, изображенных на рис. 8.5, p / q = 4 / 2 = 2 /1 (a), p / q = 2 / 6 =1/ 3 (б), p / q = 6 / 8 = 3 / 4 (в) соответственно.

Отметим, что чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. При p / q =1 мы возвращаемся к рассмотренному в § 3 частному случаю фигур Лиссажу – результату сложения взаимно перпендикулярных колебаний одинаковой частоты.

107

Лекция 9

3.3. Затухающие и вынужденные колебания

§ 1. Затухающие колебания

Рассмотрим примеры возникновения затухающих колебаний в колебательных системах различной физической природы.

Упругий маятник. Пусть тело массы m, прикрепленное к пружине жесткости k, будучи выведенным из равновесного положения, совершает малые колебания в направлении x (рис. 9.1). Кроме силы упругости Fe = −kx на тело действует также сила сопротивления среды, пропорциональная скорости движения и направленная противоположно вектору скорости: Fr = −rx , где r – коэффициент сопротив-

ления. Вес тела скомпенсирован силой реакции опоры: mg = −N .

N

Fe Fr

m g

Рис. 9.1. Упругий маятник в условиях сопротивления среды

108

Уравнение движения такого упругого маятника можно записать в виде

mx = −kx −rx.

Собрав все члены в левой части уравнения и поделив на коэффициент при старшей производной, получаем

та затухающих колебаний.

Колебательный контур. Пусть колебательный контур, рассмотренный в § 3 лекции 7, содержит кроме конденсатора и катушки индуктивности последовательно включенный с ними резистор, вносящий активное сопротивление R (рис. 9.2).

C L

Рис. 9.2. Колебательный контур, содержащий активное сопротивление

109

Тогда, в соответствии со вторым правилом Кирхгофа, сумма падений напряжения на конденсаторе и резисторе должна равняться ЭДС самоиндукции в катушке:

где β = R / (2L) , а ω0 =1/ 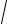LC, как и выше, обозначают соответственно коэффициент затухания и циклическую частоту незатухающих колебаний (теперь уже заряда на обкладках конденсатора). По аналогии с (9.2) уравнение затухающих колебаний в рассматриваемом колебательном контуре имеет вид

где Qm0 теперь обозначает начальную амплитуду, а ω = ω02 − β2 , как и прежде, циклическую частоту затухающих колебаний ( β <ω0 ).

Уравнения (9.1) и (9.3), равно как и их решения (9.2) и (9.4), математически эквивалентны. Между ними существует глубокая физическая аналогия, отраженная в табл. 9.1, что позволяет представить дифференциальное уравнение затухающих колебаний в обобщенной форме:

110