Физика [РТФ, Браже & Долгов, 1 семестр] / Шизика

правления векторов углового ускорения и угловой скорости противоположны друг другу: ε ↑↓ω.

Из рис. 1.2 следует, что перемещение рассматриваемой материальной точки за время dt по дуге окружности радиуса ri

dli = rdi ϕ .

Тогда линейная скорость этой материальной точки

(см. рис. 1.2), выражение (1.14) в векторной записи должно быть представлено в виде

Кинетическая энергия нашей материальной точки с учетом выражения (1.14) может быть записана в виде

Ki = m2ivi2 = mir2i2ω2 .

Величина

называется моментом инерции материальной точки относительно оси вращения. Тогда выражение для кинетической энергии вращения материальной точки принимает вид

31

По аналогии с моментом силы, известным вам из школьного курса физики как произведение силы на плечо, или, в векторной запи-

си, как M = rF , введем понятие момента импульса материальной точки

Здесь, согласно (1.3), pi = mivi – импульс этой материальной точки. По аналогии импульсом момент импульса (1.18) может быть записан в виде

Продифференцируем выражение (1.18) по времени:

Дифференцируя по времени выражение (1.19), в предположении Ii = const,c учетом (1.13) получаем

32

Сравнивая (1.20) и (2.21), можем записать

Выражение (1.21) является аналогом второго закона Ньютона (1.5) для вращательного движения материальной точки, а (1.22) представляет собой частный случай этого закона, когда ее момент инерции не изменяется в процессе вращения.

Вращение твердого тела. Обобщим теперь выражения (1.18)– (1.20), (1.22) на случай сплошного твердого тела. Для этого мы должны взять пределы сумм соответствующих величин по всем материальным точкам, устремляя их число в бесконечность:

т. е. момент инерции твердого тела

33

так как

по аналогии с векторной суммой всех внутренних сил в системе. Полученное выражение

носит название основного уравнения динамики вращательного движения твердого тела. Его частный случай для постоянного момента инерции тела легко получается суммированием (1.22) и имеет следующий вид:

Пример. Рассмотрим применение формулы (1.23) к задаче отыскания момента инерции тонкого длинного стержня, вращающегося относительно оси, проходящей через один из его концов под произвольным углом (рис. 1.3).

z

r = l sin α

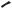dl

α l L

0

Рис. 1.3. К выводу момента инерции стержня

34

Объем элемента стержня длиной dl dV = Sdl , где S – площадь его поперечного сечения. Тогда момент инерции всего стержня относительно выбранной оси

Если ось вращения перпендикулярна стержню (α =π / 2) , то

Чтобы найти момент инерции тела относительно другой оси, следует воспользоваться теоремой Штейнера:

Момент инерции тела относительно некоторой оси вращения равен моменту инерции этого тела относительно оси, проходящей параллельно данной оси через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями:

I = I0 + mb2.

Таким образом, на практике достаточно знать, как вычисляется момент инерции тела относительно оси, проходящей через его центр масс. Для рассмотренного выше стержня момент инерции относительно оси, проходящей через его середину (центр масс) перпендикулярно стержню, воспользовавшись теоремой Штейнера, можно найти как

35

В табл. 1.2 приведена аналогия межу соответствующими кинематическими и динамическими характеристиками поступательного и вращательного движений.

Таблица 1.2

Характеристики поступательного и вращательного движений

36

Лекция 2

1.2. Законы сохранения

§ 1. Теорема Нётер

Немецкий математик Эмми Нётер в 1918 г. доказала теорему, оказавшую большое влияние на понимание природы законов сохранения ряда физических величин, увязав их со свойствами симметрии пространства и времени. Вот ее формулировка:

Если система сохраняет свои свойства при каком-либо преобразовании переменных, то в ней действует закон сохранения некоторой физической величины, связанной с данным преобразованием.

Иначе говоря, если система инвариантна относительно какихлибо преобразований пространственных координат и/или времени, то в ней обязательно должен действовать закон сохранения той физической величины, которая имеет отношение к данному преобразованию. Мы не будем здесь доказывать эту теорему. Наш предмет – физика, и перед нами стоят другие задачи. Прежде всего, попытаемся выяснить, сколько именно и каких физических величин должно сохраняться в классической механике.

Как было отмечено в лекции 1, в классической механике пространство считается трехмерным, однородным и изотропным. Оно также евклидово (не искривлено) и континуально (сплошное). Это позволяет ввести в рассмотрение некоторую систему отсчета, с которой связана декартова система из трех пространственных координат. Ее можно преобразовывать следующим образом: или транслировать

37

(осуществлять пространственный перенос начала координат в какомлибо направлении), или поворачивать вокруг начала координат. В первом случае свойства системы не должны изменяться вследствие однородности пространства. Во втором – вследствие его изотропности.

Время в классической механике полагается одномерным и однородным. Оно евклидово, необратимо и континуально. Следовательно, можно ввести понятие «стрелы времени», направленной из начала его отсчета в будущее. Единственным преобразованием такой временнóй координаты является перенос начала отсчета времени (временнáя трансляция).

Таким образом, постулируемые в классической механике

свойства симметрии пространства и времени допускают существование в ней законов сохранения трех физических величин. Рискнем предположить, что это импульс, момент импульса и энергия.

Обратите внимание: в действительности существует еще одно преобразование пространственных координат – зеркальное отражение в плоскости, переводящее правовинтовую тройку координатных осей в левовинтовую. Ему соответствует закон сохранения четности: зеркальное изображение процесса физически реализуемо с той же вероятностью, что и сам процесс. Например, если некоторое тело падает сверху вниз, на землю, то в зеркальном изображении данного процесса мы наблюдаем то же самое, а не противоположное явление – отрыв тела от земли.

Однако в макромире это настолько привычное явление, что закон сохранения четности выглядит тривиально и в классической механике обычно не упоминается.

§ 2. Закон сохранения импульса

Рассмотрим замкнутую систему из N взаимодействующих между собой тел (рис. 2.1). Это означает, что в системе действуют только внутренние силы Fi , а внешние силы отсутствуют или их действие

38

скомпенсировано: Fi(e) = 0 (i =1,2,3,...,N ). Используя свойство однородности пространства, переместим систему из первоначального положения 1 в некоторое новое положение 2 путем трансляции на произвольный вектор r.

Рис. 2.1. Трансляция замкнутой системы тел не изменяет их взаимного распо-

ложения в пространстве, а также мгновенных значений скоростей движения ( vi = const ) и кинетической энергии системы в силу однородности пространства

Работа внутренних сил по перемещению системы

A12 = ∑N Fi r = 0,

i=1

так как приращения кинетической энергии системы при этом не происходит. Поскольку вектор трансляции r произвольный, то из записанного выражения следует, что

i=1

т. е. векторная сумма всех внутренних сил в замкнутой системе равна нулю. Как было показано в лекции 1, это утверждение эквивалентно третьему закону Ньютона. Таким образом, третий закон Нью-

39

тона, который мы ранее рассматривали как постулат классической механики, фактически является следствием однородности пространства.

Запишем теперь второй закон Ньютона для i-го тела, имея в виду его центр масс:

dpdti = Fi .

Просуммируем это выражение по всем i от 1 до N с учетом (2.1):

где P – полный импульс системы. Отсюда следует, что

Полный импульс замкнутой системы тел с течением времени не изменяется.

Данное утверждение называется законом сохранения импульса. Как видим, этот закон обусловлен инвариантностью системы относительно пространственных трансляций или, что одно и то же, является следствием однородности пространства.

§ 3. Закон сохранения момента импульса

Вернемся к рассмотрению описанной в предыдущем параграфе замкнутой системы тел, полагая теперь, что действующие на них внутренние силы Fi создают моменты сил Mi = ri Fi , где ri – ради-

40