Физика [РТФ, Браже & Долгов, 1 семестр] / Шизика

Таблица 9.1

Аналогия в описании механических и электромагнитных колебаний

111

Как видно из табл. 9.1, индуктивность в электромагнитных процессах играет ту же роль, что и масса в механических явлениях – это мера инерции системы: согласно правилу Ленца, ЭДС самоиндукции (тем бóльшая, чем больше индуктивность) всегда действует таким образом, чтобы препятствовать причине, ее вызывающей. Величина, обратная емкости конденсатора, аналогична жесткости пружины или коэффициенту квазиупругой силы, возвращающей систему к положению равновесия. Активное сопротивление аналогично коэффициенту сопротивления среды.

На рис. 9.3 представлены графики затухающих механических колебаний (для случая β <ω0 ) и апериодического затухания (для случая β ≥ω0 ).

Рис. 9.3. Графики затухающих колебаний (а) и апериодического затухания (б).

Случаи 1 и 2 отличаются величиной затухания: в первом случае система может совершить однократный переход через положение равновесия, а во втором – затухание настолько велико, что система не успевает совершить даже одного полупериода колебаний.

§ 2. Характеристики затухающих колебаний

Наряду с коэффициентом затухания β для количественного описания величины затухания в теории колебаний используется ряд других характеристик.

112

Как следует из (9.2), (9.4), (9.6), отношение двух последовательных амплитуд, отличающихся по времени на один период колебаний,

Эта величина называется декрементом колебаний (от лат. decrementum – уменьшение), а ее логарифм – логарифмическим декрементом колебаний:

уменьшается в «e» раз. Такое время принято называть временем релаксации колебательной системы. Используя время релаксации, выражение (9.8) можно переписать в виде

где Ne – число колебаний, за которое амплитуда убывает в «e» раз. Часто пользуются также понятием добротность колебательной

системы. Эта величина представляет собой умноженное на 2π отношение энергии, запасенной в системе, к средней энергии потерь за период колебаний (т. е. к средней рассеиваемой мощности, умноженной на период колебаний):

113

Средняя мощность рассеяния, с учетом сделанного в § 1 допущения о пропорциональности силы сопротивления скорости (на примере механических колебаний),

PS = −FS x = r x2 = 2βmω2 A02 e−2βt sin2 (ω0t +ϕ0 ) .

Вслучае слабого затухания показательная функция изменяется значительно медленнее, чем квадрат синуса, что позволяет вывести ее за знак усреднения, а среднее за период значение квадрата синуса равно 1/2. Поэтому

PS = 2βmω2 A02e−2βt 12 = 2β 12 kA2 (t) = 2βE.

Тогда выражение (9.10) можно представить в виде

т. е. в случае слабо затухающих колебаний добротность колебательной системы пропорциональна числу колебаний, совершаемых системой за время, в течение которого их амплитуда убывает в «е» раз.

Типичные значения добротности некоторых колебательных систем представлены в табл. 9.2.

Таблица 9.2

Добротность некоторых колебательных систем

114

§ 3. Вынужденные колебания

Вынужденными колебаниями называют такие колебания,

которые происходят под действием внешней периодически изменяющейся вынуждающей силы.

Если вынуждающая сила изменяется во времени по гармоническому закону:

F = F0 cosωst ,

где ωs – частота вынуждающей (стимулирующей) силы, то в случае слабого затухания уравнение динамики для механической колебательной системы можно записать в виде

mx = −kx −rx + F0 cosωst

или, после деления на коэффициент при старшей производной,

где β = r / (2m) , ω0 = k / m , f0 = Fm0 .

Общее решение неоднородного дифференциального уравнения (9.12), как доказывается в математике, складывается из общего решения соответствующего однородного уравнения (когда правая часть равна нулю) и частного решения данного неоднородного уравнения. Общее решение однородного уравнения, как было показано в § 1, представляет собой затухающие колебания вида (9.2). Его вклад играет заметную роль лишь на начальной стадии процесса, когда колебания еще не установились. С течением времени, вследствие затухания, роль этого слагаемого все более уменьшается,

115

и установившиеся колебания описываются лишь частным решением уравнения (9.12). Как доказывается в математике, оно имет вид

§ 4. Резонанс

Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний системы.

Для того чтобы определить точное значение резонансной частоты, нужно найти условие максимума амплитуды в уравнении вынужденных колебаний (9.13) или, что одно и то же, условие минимума выражения, стоящего под знаком корня в ее знаменателе. Продифференцировав его по переменной ωs и приравняв результат нулю, получаем

−4(ω02 −ωs2 )ωS +8β2ωs = 0.

Данное уравнение имеет три корня:

ωs = 0 и ωs = ±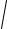ω02 − 2β2 ,

первый из которых является условием максимума, а не минимума, а отрицательный корень, как не имеющий физического смысла, должен быть отброшен. Таким образом, частота, на которой имеет место резонанс величины x ,

116

Подставляя (9.14) в амплитуду вынужденных колебаний, описываемых уравнением (9.13), получаем выражение для резонансной амплитуды:

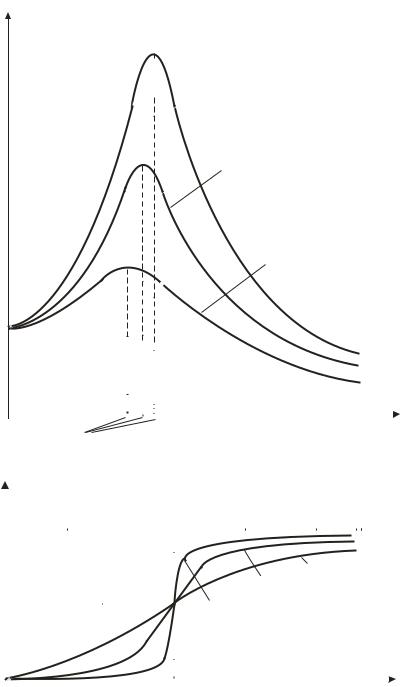
отсутствии затухания (β = 0) резонансная частота совпадает с частотой собственных колебаний системы, а резонансная амплитуда обращается в бесконечность. Графики зависимости амплитуды вынужденных колебаний A и сдвига фаз ϕ смещения x относительно вынуждающей силы F от ее частоты ωs представлены на рис. 9.4.

При ωs → 0 все резонансные кривые стремятся к предельному значению A = f0 / ω02 = F0 / k . При ωs → ∞ они асимптотически стремятся к нулю (система не успевает отклониться от положения равновесия). Наконец, чем меньше затухание и выше добротность колебательной системы, тем больше значение резонансной амплитуды Ares .

Как следует из (9.13), смещение отстоит по фазе от вынуждаю-

щей силы в пределах от 0 до π (рис. 94, б). При резонансе (ωs =ωres ) этот фазовый сдвиг ϕ ≤π / 2 достигает значения π / 2 при β = 0).

Обратите внимание: мы исследовали здесь лишь случай резонанса смещений для механических колебаний. Похожим образом возникает резонанс заряда и напряжений в колебательном контуре, как можно догадаться, рассматривая табл. 9.1. Однако, поскольку вынужденные колебания присущи также производной смещения по времени (скорости) и производной заряда по времени (току), то существуют и резонанс скоростей, и резонанс токов. Они наблюдаются на других частотах, чем резонансы смещений и напряжений.

117

β1

β2

β3

f0 /ω20