еме dV пропорциональна величине этого объема и интенсивности I дебройлевской волны частицы, которая, в свою очередь, пропорциональна квадрату амплитуды этой волны:
dP(r,t) IdV ; I A2 = ΨΨ* = |
|
Ψ |
|
2 . |
(16.16) |
|
|
Отсюда следует, что квадрат модуля волновой функции частицы равен плотности вероятности ее обнаружения в данной точке пространства в данный момент времени:
|
|
|
2 |
|
dP(r,t) |
|
|
|
|
|
|
|
Ψ(r,t) |
|
|
= |
|
= w(r,t). |
(16.17) |
|
|
|
dV |
|
|
|
|
|
|
|
Вероятность обнаружить частицу во всем объеме V ее возможной локализации, естественно, равна единице:
V∫w(r,t)dV =1.
Следовательно,
Выражение (16.18) называется условием нормировки волновой функции.
Из структуры уравнения Шредингера и вышеприведенных рассуждений ясно, что волновая функция должна обладать следующими свойствами:
–однозначность,
–непрерывность,
–непрерывная диффренцируемость (гладкость),
–нормируемость.
Таким образом, относительно природы волн де Бройля и описывающей их волновой функции можно сделать вывод, что это волны вероятности: в них колеблется вероятность обнаружения микрочастицы в рассматриваемом месте.
Обратите внимание: как и законы Ньютона, уравнение Шредингера ниоткуда не выводится. Оно просто подобрано таким образом, чтобы ему удовлетворяло уравнение бегущей волны де Бройля. Поскольку существование волн де Бройля подтверждается опытным путем, то уравнение Шредингера, таким образом, не противоречит опыту и может быть постулировано как основополагающее уравнение квантовой механики.
§ 4. Прохождение частицы через потенциальный барьер
Рассмотрим прямоугольный потенциальный барьер высотой U0 и шириной a (рис. 16.2а), на который налетает микрочастица с энергией E <U0 .
U U0
U0
Е< U0
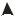 Re ψ( ) x
Re ψ( ) x
Рис. 16.2. Прохождение частицы через прямоугольный потенциальный барьер:
а – вид барьера, б – вид волновой функции частицы вне и внутри барьера
По законам классической физики такая частица не может преодолеть барьер и проникнуть из области I через область II в область III, так как в области II ее импульс является мнимой величиной:
p= 
 2mK =
2mK = 
 2m(E −U0 ) =i
2m(E −U0 ) =i
 2m(U0 −E).
2m(U0 −E).
Вквантовой механике следует рассматривать волны де Бройля
ψ (x)= Aei px,
причем в областях I–III эти волны, соответственно, имеют вид
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
ψ |
|
|
(x) = A e |
|
|
|
2mE x , |
|
(16.19) |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
|
|
|
|
|
x |
|
|
ψ |
|
(x) = A e |
|
2m(U0 −E ) |
, |
(16.20) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
ψ |
|
|
(x) = A e |
|
|
2mE x . |
|
(16.21) |
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Графики этих волн представлены на рис. 16.2б.
Выражение (16.20) показывает, что внутри барьера амплитуда дебройлевской волны частицы экспоненциально уменьшается, но для барьера конечной ширины вероятность обнаружить частицу за барьером отлична от нуля. Такое проникновение частицы через барьер на-
зывается туннельным эффектом.
Коэффициент прозрачности барьера можно найти как отношение вероятности нахождения частицы за барьером к вероятности ее нахождения перед барьером:
|
|
ψ |
|
(a) |
|
|
2 |
|
−2 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
D = |
|
2 |
|
|
|
≈e |
2m(U |
−E) |
. |
(16.22) |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ψ2 |
(0) |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначив 2mE / 2 =k2 , сведем выражение (16.23) к уравнению Гельмгольца
d2ψ |
2 |
|
|
+k ψ =0, |
(16 .25) |
dx2 |
решение которого имеет вид
Из граничных условий (16.24) следует, что
α = 0, k = ±nπ / a ( n =1, 2, 3, ...). |
(16.27) |
Подставляя в ( 16.27) обозначение для k , находим величины разрешенных значений энергии частицы:
|
E |
= |
π2 2 |
n2. |
(16.28) |
|
2ma2 |
|
n |
|
|
|
C учетом (16.27) для стационарных состояний частицы в яме решение уравнения Шредингера (16.26) принимает вид
ψn (x)= Asin nπ x. |
(16.29) |
a |
|
Амплитуду A волновой функции можно найти из условия нормировки (16.18), записав его для одномерного случая:
2 a |
2 nπ |
|
1 |
|
|
|
2 |
A = |
2 |
|
A |
∫sin |
a |
xdx =1; A |
2 a =1; |
a. |
|
0 |
|
|
|
|
|
|
Таким образом, n-е стационарное состояние частицы описывается решением
n x |
2 sin n x. |
(16.30) |
|
a |
a |
|
Соответствующее ему частное решение временного уравнения Шредингера можно записать в виде
|
i |
2 sin n x e |
i |
|
Ψn x,t n x,t e |
|
Ent |
|
Ent. |
(16.31) |
|
|
|
|
|
a |
a |
|
|
|
|
Общее решение, описывающее переход между n-м и m-м стационарными состояниями, представляется в виде линейной комбинации соответствующих частных решений:
Ψnm x,t |
a |
Ψn x,t Ψm x,t . |
(16.32) |
|
2 |
|
|
|
Плотность вероятности обнаружения частицы в точке x в момент времени t, согласно (16.17), (16.32),
|
|
|
wnm |
|
Ψnm x,t |
|
2 |
|
i |
|
|
|
|
|
|
|
|
|
sin2 |
n x sin2 |
m x 2sin n xsin m x e |
(En Em)t |
|
|
|
|
a |
a |
|
|
a |
a |
|
|
|
колеблется с частотой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En Em |
. |
|
|
(16.33) |
|
|
|
|
|
|
|
|
|
nm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
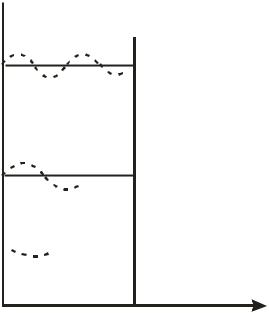
Из (16.31) и рис. 16.3 видно, что стационарным состояниям частицы соответствуют стоячие волны де Бройля. При переходе из одного стационарного состояния в другое происходит излучение или поглощение кванта энергии частотой nm , определяемой выражением
(16.33).
206
§ 6. Линейный гармонический осциллятор
Рассмотрим теперь частицу, находящуюся в параболической потенциальной яме (рис. 16.4) вида
 U, En
U, En
n = 5 n = 4 n = 3 n = 2
n = 1
n = 0
Рис. 16.4. Схема энергетических уровней частицы в параболической потен-
циальной яме
Из теории колебаний (см. § 1 лекции 7) следует, что в этом случае частица будет совершать гармонические колебания с частотой ω =
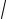 k / m . По аналогии с прямоугольной потенциальной ямой можно предположить, что из-за локализации частицы в ограниченной области пространства снова будут иметь место дискретные по энергии состояния частицы в яме.
k / m . По аналогии с прямоугольной потенциальной ямой можно предположить, что из-за локализации частицы в ограниченной области пространства снова будут иметь место дискретные по энергии состояния частицы в яме.
Уравнение Шредингера в данном случае имеет вид
d2ψ |
|
2m |
mω2x2 |
|
|
|
+ |
|
|
E − |
|
ψ =0. |
(16.35) |
dt |
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Для параболических граничных условий оно приводит к стационарным энергетическим состояниям с энергией
En = n + |
1 |
ω |
(n =0, 1, 2, 3, …). |
(16.36) |
|
2 |
|
|
|
При n =0 E0 = ω / 2. Это так называемая энергия нулевых колебаний одномерного (линейного) гармонического осциллятора. Существование таких колебаний связано с волновой природой микрочастиц и может быть обосновано с помощью соотношения неопределенностей Гейзенберга (16.5).
В данном случае
x = 
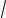 2x, p =
2x, p = 
 2 p,
2 p,
где x и p – соответственно средние по времени (действующие) значения координаты и импульса частицы. Таким образом,
x2 p2 ≥ 42 .
С другой стороны,
|
|
E = K +U = |
p2 |
+ mω2 |
x2 ≥ |
p2 |
+ mω2 2 . |
|
|
|
|
|
|
|
|
2m |
|
2 |
|
2m |
|
|
8p2 |
|
|
Найдем Emin : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂E |
=0; |
|
1 |
|
− mω2 22 |
=0; |
(p2 )2 = |
m2ω2 2 |
; |
p2 = mω ; |
|
|
|
|
|
∂(p2 ) |
|
2m |
|
|
|
|
8(p2 ) |
|
|
|
|
|
4 |
|
2 |
|
|
|
E |
= E = 1 |
ω+ 1 ω = 1 |
ω. |
|
|
|
|
|
|
min |
0 |
4 |
|
4 |
|
2 |
|
|
|
Обратите внимание: в отличие от прямоугольной потенциальной ямы, где энергия стационарных состояний увеличивается с ростом n по квадратичному закону, в параболической потенциальной яме энергетические уровни расположены эквидистантно.
Лекция 17
5.2. Физика атомов и молекул
§ 1. Атом водорода
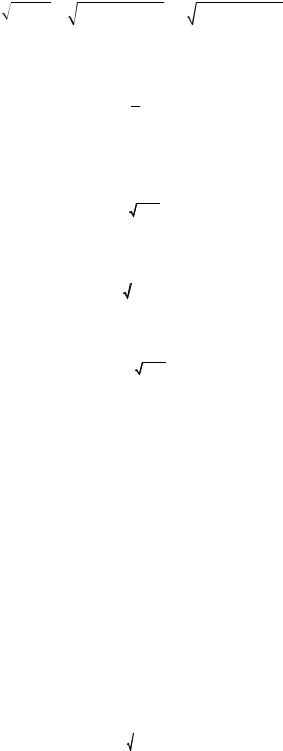
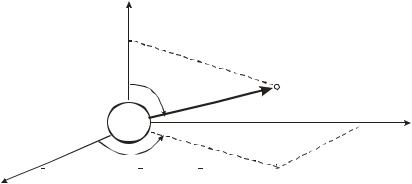
Атом водорода (Н), а также водородоподобные ионы (Не+, Li2+ и др.) являются наиболее простыми атомными системами. В них единственный электрон удерживается вблизи ядра с зарядом Ze, где Z – порядковый номер соответствующего химического элемента (рис. 24.1). По сути дела, электрон удерживается в некоторой бесконечно глубокой сферической потенциальной яме. Следовательно, как и в §§ 5, 6 прошлой лекции, мы можем ожидать, что электрон в таких системах будет иметь дискретный набор возможных значений энергии.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rcosθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ |
|
r |
|
|
|
|
|
|
|
|
|
|
|
Ze |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rsinθsinϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rsinθcosϕ |
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 17.1. Сферические координаты электрона в водородоподобной системе
Стационарное уравнение Шредингера (16.14) для рассматриваемой системы имеет вид
∆ψ + 2m |
E −U ψ =0, |
(17.1) |
2 ( |
) |
|
где
U = − 1 Ze2
4πε0 r
−потенциальная энергия электрона в электрическом поле ядра.
Вуравнении (17.1) следует перейти к сферическим координатам и решить его в предположении, что кинетическая энергия электрона
меньше, чем потенциальная энергия, взятая по модулю: K < U , ина-
че электрон не будет удерживаться ядром. Ввиду возникающих при этом математических трудностей, мы опустим сам процесс решения, а обсудим лишь получающиеся результаты.
Полная энергия электрона, находящегося в атоме (ионе),
E = 12 mv2 − 4πε1 0 Zer 2 ,
естественно, отрицательна. Шредингер показал, что она может принимать лишь дискретные значения:
En = − |
me4 |
|
Z 2 |
(n =1, 2, 3, …). |
(17.2) |
|
2 |
|
2 |
2 |
n |
|
|
|
8h ε0 |
|
|
|
Из сферической симметрии задачи следует, что ее решение |
можно представить в виде |
|
|
|
|
|
ψnlm (r,θ,ϕ)=Rn (r)Ylm (θ,ϕ), |
(17.3) |
где Rn (r)  радиальная компонента решения, выражаемая через полиномы Лагерра; Ylm (θ,ϕ) – угловая компонента решения, выражае-
радиальная компонента решения, выражаемая через полиномы Лагерра; Ylm (θ,ϕ) – угловая компонента решения, выражае-





 U
U






 U, E
U, E n =
n = 



 n =
n = 







 n =
n = 










 n =
n =  U, E
U, E

 2
2
 2
2  радиальная компонента решения, выражаемая через полиномы Лагерра; Y
радиальная компонента решения, выражаемая через полиномы Лагерра; Y