Физика [РТФ, Браже & Долгов, 1 семестр] / Шизика

где коэффициент электропроводности

Уравнение (20.14) – это не что иное, как известный нам закон Ома в дифференциальной форме (см. § 6 лекции 4). Действительно, dq / dt = I – сила тока, I / S = j – плотность тока, −dϕ / dx = E – напряженность электрического поля. Следовательно, (20.14) эквивалентно выражению

j =σ E .

Завершая данный параграф, заметим, что величина, переносимая через некоторую площадку в единицу времени, называется потоком этой величины, а поток, приходящийся на единицу площади, называется плотностью потока. Таким образом, jΨ = dΨ / (Sdt) – это плот-

ность потока переносимой величины Ψ . Тогда из обобщенного уравнения явлений переноса (20.6) следует, что плотность потока дина-

мического параметра системы (массы, импульса, теплоты, заряда и т. п.) пропорциональна взятому со знаком «минус» градиенту некоторого обобщенного потенциала этой системы (плотности, скорости, температуры, электрического потенциала и т.п.):

jΨ = −λ ddxΦ ,

где λ – некоторый коэффициент пропорциональности (кинетический коэффициент). Это так называемый принцип линейности, сформулированный в 1931 г. американским химиком и физиком норвежского происхождения Л. Онсагером.

261

Лекция 21

6.3. Начала термодинамики

§ 1. Первое начало термодинамики

Термодинамика – это раздел физики, изучающий связи и взаимопревращения различных видов энергии, теплоты и работы в макроскопических системах.

Термодинамика основывается на установленных опытным пу-

тем законах, называемых началами термодинамики.

Первое начало термодинамики представляет собой обобщение закона сохранения энергии, первоначально сформулированного для механических систем, на тепловые процессы:

Количество теплоты, сообщенное системе, расходуется на изменение ее внутренней энергии и работу, совершаемую системой против внешних сил.

В дифференциальной форме первое начало термодинамики можно записать следующим образом:

где δQ – количество теплоты, сообщенное системе, dU – изменение

внутренней энергии, δ A – работа, совершаемая системой. Здесь нами учтено, что внутренняя энергия является функцией состояния системы. Поэтому ее бесконечно малое изменение описывается полным дифференциалом ( d ). Количество теплоты и совершаемая работа зависят от вида термодинамического процесса, т. е. являются функция-

262

ми процесса. Поэтому и бесконечно малое количество сообщаемой теплоты, и бесконечно малая величина совершаемой при этом работы обозначаются как неполные дифференциалы или функционалы (δ ).

Обратите внимание: количество теплоты нельзя рассматривать как количество какой-то энергии, содержащейся в системе. Это динамическое понятие, которое проявляется лишь в процессе. Говорить о количестве содержащегося в теле тепла столь же бессмысленно, как и говорить о содержании в нем работы.

О возможности превращения теплоты в работу впервые заявил немецкий врач Ю. Р. Майер в 1841 г. В 1843 г. английский физик Дж. Джоуль экспериментально доказал, что теплоту можно получить за счет механической работы, и вычислил механический эквивалент теплоты. Наконец, в 1847 г. немецкий естествоиспытатель Г. Гельмгольц сформулировал и математически обосновал закон сохранения энергии и отметил его всеобщий характер, показав, что ему подчиняются не только механические, но и тепловые, электрические, физиологические и другие процессы.

Функционал количества теплоты δQ в (21.1) можно связать с изменением температуры, введя понятие теплоемкости системы:

Теплоемкостью термодинамической системы называется физическая величина, равная отношению количества теплоты, сообщенного системе, к вызванному этой теплотой изменению ее температуры:

C = δdTQ .

Различают удельную теплоемкость или теплоемкость, приходящуюся на единицу массы вещества:

c = 1 δQ m dT

и молярную теплоемкость или теплоемкость, приходящуюся на один моль вещества:

Cµ =ν1 δdTQ .

263

(V = const ), как следует из (21.3), работа не совершается: A = 0 . Изобарический процесс. В условиях изобарического процесса

( p = const ) (21.3) приводит к следующему выражению для совершае-

Дифференциал внутренней энергии в (21.1), согласно формуле (20.2) из прошлой лекции, dU = (i / 2)ν RdT , откуда

Используя (21.2)–(21.4), первое начало термодинамики можно записать в интегральной форме:

264

§ 2. Классическая теория теплоемкостей

Перепишем первое начало термодинамики (21.1) в виде

Первое слагаемое в правой части (21.6) соответствует изменению внутренней энергии идеального газа, поэтому все выводы, сделанные на основе этого выражения, также будут относиться к идеаль-

Изобарический процесс. При p = const из уравнения Клапей-

рона – Менделеева следует, что pdV =ν RdT , и (21.6) приводится к виду

откуда молярная теплоемкость идеального газа при постоянном давлении

Из (21.8) также следует формула Майера, связывающая молярные теплоемкости идеального газа при постоянном объеме и при постоянном давлении:

265

Поделив (21.9) на (21.7), найдем так называемый показатель адиабаты, входящий в уравнение адиабатического процесса (см. ниже):

Изотермический процесс. В соответствии с определением молярной теплоемкости, при T = const

Адиабатический процесс. В отсутствие теплообмена с окружающей средой δQ = 0, как следует из того же определения,

Молярную теплоемкость для адиабатического процесса мы обозначили как теплоемкость при постоянной энтропии, так как в этом процессе dS =δQ / T (см. § 4 лекции 19).

Теплоемкость твердых тел. В сравнении с газами твердые тела обладают очень малой сжимаемостью, поэтому работой расширения можно пренебречь, положив в (21.6) pdV = 0. Каждый атом в кр и- сталлической решетке твердого тела обладает i = 2nкол = 3 3 = 6 степенями свободы. Тогда из ( 21.6) следует, что молярная теплоемкость твердого тела вычисляется по формуле

Это так называемый закон Дюлонга и Пти, открытый экспериментально французскими учеными П. Л. Дюлонгом и А. Пти в 1819 г. и хорошо описывающий теплоемкости твердых тел при достаточно высоких температурах. Ввиду зависимости числа степеней свободы от температуры (см. § 1 лекции 20) формула (21.17) приводит к не-

266

верным (завышенным) значениям теплоемкости твердых тел в области низких температур. Строгая теория теплоемкости твердых тел может быть построена лишь на основе квантовых представлений о колебаниях кристаллической решетки.

§ 3. Теорема Карно

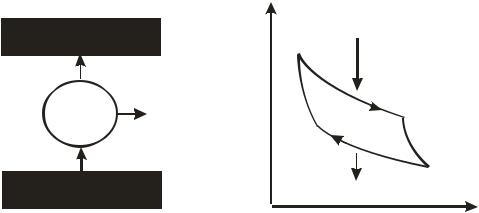
Любой тепловой двигатель, работающий по повторяющемуся циклу, состоит из трех основных элементов: нагревателя, рабочего тела и холодильника (рис. 21.1а).

Рис. 21.1. Схема работы тепловой машины (а) и цикл Карно (б) для

идеальной тепловой машины

В каждом цикле рабочее тело (например, пары какого-нибудь топлива) получает от нагревателя количество теплоты Q1 и отдает холодильнику количество теплоты Q2 < Q1 . За счет разности этих количеств теплоты совершается работа. Коэффициент полезного действия (КПД) любой тепловой машины, таким образом, определяется следующим выражением:

267

Q1

Возникает вопрос: каков предельно достижимый КПД произвольной тепловой машины? Ответ на этот вопрос был дан в 18 24 г. французским инженером Н. Карно. Карно показал, что КПД идеальной тепловой машины, т. е. теплового двигателя, в котором отсутствуют потери на трение, излучение и другие процессы, связанные с необратимостью превращения энергии, независимо от природы рабочего тела, определяется исключительно температурой нагревателя (Т1) и температурой холодильника (Т2).

В качестве идеального рабочего цикла Карно предложил цикл (рис. 21.1б), состоящий из двух изотерм (1–1, 3–4) и двух адиабат (2–3, 4–1). Изотермический процесс является обратимым, так как должен быть бесконечно медленным процессом, чтобы в системе не успевали возникать градиенты температуры. Адиабатический процесс обратим, наоборот, в силу требования своей бесконечной быстроты, чтобы в системе не успевал произойти теплообмен.

Количество теплоты, переданной от нагревателя рабочему телу на участке его изотермического расширения

Q1 = A12 =ν RT1 ln V2 .

V1

В свою очередь, количество теплоты, отданное рабочим телом холодильнику на участке изотермического сжатия

Q2 = A34 =ν RT2 ln V4 .

V3

268

Уравнения адиабат для участков расширения и сжатия рабочего тела, соответственно, имеют вид

Из четырех последних уравнений несложно получить формулу для КПД тепловой машины, работающей по циклу Карно:

Математически теорему Карно можно записать в виде

где знак равенства соответствует обратимым циклам, а знак неравенства – необратимым циклам.

§ 4. Второе начало термодинамики

Если первое начало термодинамики представляет собой распространение закона сохранения энергии на тепловые процессы (см. §1 настоящей лекции), то второе начало термодинамики устанавливает направление протекания тепловых явлений. Исторически было дано несколько качественных формулировок этого начала. Р. Клаузиус дал следующую формулировку: «Теплота не может самостоятельно переходить от менее нагретого тела к более нагретому телу». М. Планк связал второе начало термодинамики с принципиальными особенно-

269

стями протекания циклических процессов: «Невозможен такой периодический процесс, единственным результатом которого было бы превращение теплоты в работу». Теорема Карно позволяет придать этим формулировкам количественный характер.

Запишем неравенство (21.20) в виде

Q1 ≤ Q2 .

T1 T2

Поскольку Q2 – теплота, которая отнимается от рабочего тела, то, с учетом знака этой величины, последнее выражение можно записать следующим образом:

Q1 + Q2 ≤ 0

T1 T2

или

∑N Qi ≤ 0.

i=1 Ti

При непрерывном изменении состояния рабочего тела по произвольному циклу сумма перейдет в интеграл по замкнутому контуру:

Выражение (21.18) называется неравенством Клаузиуса.

Клаузиус назвал отношение количества сообщенного телу теплоты к температуре приведенной теплотой. Из ( 21.21) вытекает, что можно ввести некоторую функцию состояния термодинамической системы, изменение которой связно с изменением полученной системой приведенной теплоты следующим образом:

270