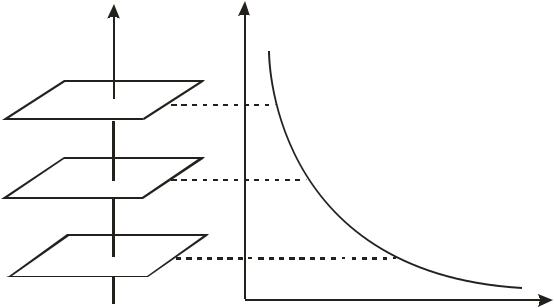
Рис. 20.1. Возможные степени свободы молекул
Из рис. 20.1 ясно, что двухатомные молекулы могут иметь три поступательные, две вращательные (вращение вокруг третьей координатной оси ничего нового не вносит) и одну колебательную степень свободы.
Таким образом, максимальное число степеней свободы двухатомной молекулы, согласно вышеприведенной формуле, равно семи. Трех- и более атомные молекулы могут иметь три поступательные, три вращательные (если атомы не расположены на одной прямой) и несколько колебательных степеней свободы, число которых зависит от количества атомов в молекуле, их взаимного расположения и возможных типов колебаний.
Обратите внимание: число степеней свободы молекул газа зависит от его температуры. При низких температурах молекулы газа могут совершать лишь поступательное движение. С увеличением температуры газа молекулы постепенно вовлекаются во вращательное движение. При дальнейшем увеличении температуры в молекулах, также постепенно, начинают проявляться колебательные движения. Однако до температур порядка 1000 К молекулы большинства газов еще можно считать жесткими. Тогда для двухатомных газов i = 5, а для трех- и более атомных
i = 6 .
251
Вернемся к средней энергии молекул. Из вышеприведенных рассуждений ясно, что в общем случае средняя энергия одной молекулы определяется выражением
Внутренняя энергия идеального газа складывается из энергии всех его молекул:
U = ε N = 2i kTNAν ,
где NA – число молекул в одном моле (число Авогадро), а ν – число молей газа. Поскольку kNA = R , где R – универсальная газовая постоянная, то окончательно выражение для внутренней энергии идеального газа можно представить в виде
|
U =ν |
i |
RT . |
(20.2) |
|
2 |
|
|
|
|
|
В случае, если идеальный газ состоит из смеси |
m различных |
компонентов,
U= 1 RT ∑m ikνk , 2 k=1
где ik и νk соответственно число степеней свободы и число молей k-го компонента.
§ 2. Основное уравнение молекулярно-кинетической теории
Пусть имеется сосуд сферической формы, в котором находится N молекул идеального газа (рис. 20.2). Пусть одна из них, i-я, упруго ударяется в точке А о стенку сосуда под углом α к нормали.

Поскольку тангенциальная составляющая |
|
|
скорости молекулы при этом не изменя- |
В |
i |
ется, а нормальная составляющая изменя- |
ет свой знак на противоположный, то из- |
О |
vi |
|
менение импульса молекулы при одно- |
α α |
кратном столкновении со стенкой сосуда |
|
|
pi = mvi cosα −(−mvi cosα) = |
А |
|
Рис. 20.2. К выводу основно- |
= 2mvi cosα . |
го уравнения молекулярно- |
|
кинетической теории |
Расстояние, проходимое молекулой до следующего столкновения со стенкой сосуда,
AB = 2R cosα ,
где R – радиус сосуда. Конечно, между двумя столкновениями со стенкой сосуда наша i-я молекула могла неоднократно столкнуться с другими молекулами и изменить траекторию своего движения, но мы всегда можем считать, что в точке В оказалась именно она, так как молекулы не различимы между собой.
Число столкновений молекулы со стенкой сосуда в единицу времени
Сила, с которой i-я молекула действует на стенку сосуда, согласно второму закону Ньютона, равна изменению ее импульса в единицу времени:
Fi = piν = mvRi2 ,
а сила, действующая со стороны всех молекул,
F = 1 ∑N mvi2 .
R i=1
Чтобы найти давление газа, нужно эту силу поделить на площадь внутренней поверхности сосуда:
|
|
F |
|
1 |
N |
2 |
|
N |
2 |
|
|
1 |
N |
2 |
|
2 N |
|
|
|
|
|
|
|
|
|
|
|
|
p = |
= |
∑i=1mv2 i |
= |
(1 3)∑i=1mv3 i |
= |
|
2 ∑mvi |
= |
Eк . |
|
|
|
|
|
|
|
|
|
|
3 V |
|
|
S R 4πR |
|
|
(4 3)πR |
|
|
V 3 i=1 |
2 |
|
|
|
Так как |
N /V = n – число молекул в единице объема (концен- |
трация молекул), то последнее выражение можно переписать в виде
Формула (20.3) описывает основное уравнение молекулярнокинетической теории идеального газа, согласно которому
Давление идеального газа равно двум третьим от средней кинетической энергии поступательного движения всех молекул этого газа, находящихся в единице его объема.
Поскольку в соответствии (20.1)  Eк
Eк  = 3 / 2(kT ) , то (20.3) можно записать в более простом виде:
= 3 / 2(kT ) , то (20.3) можно записать в более простом виде:
Из выражения (20.4) следует, что
pV = nVkT = NkT =ν NAkT =ν RT ,
что нам известно как уравнение Клапейрона – Менделеева:
§3. Кинетическая теория явлений переноса в газах
Кявлениям переноса относят большую группу процессов, в которых на молекулярном уровне происходит перенос в пространстве через вещество каких-либо макровеличин. Мы остановимся здесь лишь на одномерных процессах, при которых указанный перенос
происходит в |
одном направлении, например, в направлении x |
(рис. 20.3). |
|
ψ |
x |
dx
<λ>{
<λ>{
dψ1/ dx
ψ1
Рис. 20.3. К выводу обобщенного уравнения явлений переноса
255
Пусть Ψ1 – физическая величина (масса, импульс, энергия и т. п.), переносимая каждой отдельной молекулой за счет столкновений с другими молекулами. Перенос этой величины Ψ всеми сталкивающимися молекулами за время dt через площадку площади S , перпендикулярную x , в направлении убывания Ψ1 и возрастания x
(dΨ1 / dx < 0)
dΨ↑ |
= |
1 |
|
Ψ1 |
− λ |
dΨ |
|
|
, |
6 |
nS v dt |
|
1 |
|
|
|
|
|
|
dx |
|
|
а в направлении возрастания Ψ1 и убывания x
|
|
|
1 |
|
|
|
dΨ |
1 |
|
|
dΨ↓ |
= |
|
nS v dt |
Ψ1 |
+ λ |
|
. |
|
6 |
dx |
|
|
|
|
|
|
|
Здесь n – концентрация молекул, а v – их средняя арифметическая скорость. Кроме того, сделано предположение, что в однонаправленном процессе вдоль одной из трех независимых координат участвует лишь 1/6 часть всех молекул из объема nS v dt (поровну в положительном и отрицательном направлениях оси).
Результирующий перенос величины Ψ составляет
dΨ = dΨ↑ − dΨ↓ = −13 v λ n ddxΨ1 Sdt .
Обобщенное уравнение явлений переноса можно представить в
виде
dΨ = −a dΨ1 |
Sdt , |
(20.6) |
dx |
|
|
где
− коэффициент переноса. Знак «минус» в уравнении (20.6) выражает тот факт, что перенос происходит в направлении, противоположном градиенту величины Ψ1
Диффузия. В этом случае переносимой величиной является масса: Ψ = M , причем каждая молекула переносит массу, равную массе самой молекулы: Ψ1 = m = ρ / n, где ρ – плотность газа. Тогда уравнение (20.6) принимает вид
dM = −D d ρ |
Sdt , |
(20.8) |
|
|
dx |
|
|
где |
|
|
|
|
D = |
1 |
v λ |
(20.9) |
|
3 |
|
|
|
обозначает коэффициент диффузии.
Выражение (20.8) известно как закон Фика, так как в форме
M = −D ρx S t ,
т. е. для конечных приращений параметров, оно было экспериментально установлено немецким ученым А. Фиком еще в 1855 г. Здесь мы его вывели из чисто кинетических представлений.
Обратите внимание: уравнение диффузии (20.8) описывает так называемую самодиффузию – явление переноса частиц какой-либо среды (молекул, атомов, электронов и т. п.), стремящегося выровнять имеющуюся в среде неоднородность их концентрации. Кроме этого простейшего случая диффузии могут наблюдаться и более сложные виды переноса массы: взаимная диффузия в системе из частиц разного сорта, термодиффузия (при наличии градиента температуры), электродиффузия (при наличии электрического поля) и др.

Вязкость. Переносимой величиной является импульс: Ψ = P , причем каждая молекула переносит импульс Ψ1 = p = mv , где v – скорость течения газа. Уравнение (20.6) в данном случае принимает вид
dP = − |
1 nm v λ dv |
Sdt = − |
1 |
ρ v λ dv |
Sdt |
|
3 |
dx |
|
3 |
dx |
|
или |
|
|
|
|
|
|
|
|
dP = −η dv Sdt , |
(20.10) |
|
|
|
dx |
|
|
|
где коэффициент вязкости
Выражение (20.10) фактически представляет собой закон Ньютона для внутреннего (вязкого) трения в газах и жидкостях, опубликованный им еще в 1687 г. в знаменитых «Математических началах натуральной философии». Действительно, dP / dt , согласно второму закону Ньютона, соответствует силе вязкого трения, возникающего между двумя параллельными слоями жидкости (газа) площади S при наличии градиента скорости dv / dx . Мы вывели этот закон из кинетических представлений.
Теплопроводность. Это перенос тепла: Ψ = Q, причем каждая молекула переносит количество теплоты, равное средней энергии молекул газа, т. е. Ψ1 = (i / 2)kT , где i – число степеней свободы молекулы, а k – постоянная Больцмана. Тогда (20.6) сводится к виду
dQ = −13 n 2i k v λ dTdx Sdt .

Поскольку n =N /V , а общее число молекул N в объеме V газа
может быть выражено через число молей ν |
и число Авогадро NA : |
n =ν NA /V , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
i |
k = |
i |
|
νkNA |
= |
i |
|
R |
M = |
i |
|
R |
ρ = c ρ, |
|
|
|
|
|
|
|
2 |
|
2 V |
|
|
2 µ V 2 µ |
V |
|
|
|
|
где R – универсальная газовая постоянная, µ – молярная масса газа, |
M – его фактическая масса, |
ρ – плотность, |
cV – удельная теплоем- |
кость газа при постоянном объеме. С учетом сделанных выкладок уравнение теплопроводности принимает вид
dQ = −κ dT |
Sdt , |
(20.12) |
dx |
|
|
где коэффициент теплопроводности
Уравнение (20.12) было получено французским математиком и физиком Ж. Б. Фурье в его работе «Аналитическая теория тепла», опубликованной в 1822 г., и называется законом Фурье для теплопроводности. Мы его получили из кинетических представлений как частный случай явлений переноса.
Электропроводность. В данном явлении переносится электрический заряд: Ψ = q , причем каждая частица переносит от столкновения к столкновению лишь долю заряда, участвующего в дрейфе под действием электрического поля, т. е.
Ψ1 = e We = e eϕ / 2 = e2ϕ ,
WT kT 2kT
где e – элементарный заряд, We – энергия заряда, приобретаемая им при движении в электрическом поле с текущим значением потенциала ϕ , WT = kT – энергия хаотического теплового движения заряда. Подставляя полученное выражение в (20.6), получаем
|
dq = − |
1 |
n v λ |
e2 dϕ |
Sdt . |
|
|
|
|
|
3 |
2kT dx |
|
|
|
|
Так как каждый заряд обладает тремя степенями свободы, то его средняя энергия
23 kT = m 2v2 .
Следовательно,
|
1 |
n v λ |
e2 |
= |
ne2 < λ > |
=σ , |
|
3 |
2kT |
2m < v > |
|
|
|
|
где σ – известная из классической теории электропроводности металлов (см. § 3 лекции 6) удельная электропроводность среды. Справедливости ради, следует отметить, что мы здесь допустили некоторую неточность, приравняв v2 = 3kT / m и v 2 = 8kT / (πm) . В данном случае это не является грубой ошибкой, так как сама величина σ , полученная из классической теории электропроводности, не дает точного значения удельной электропроводности.
Таким образом, уравнение электропроводности можно записать в следующем виде:
dq = −σ |
dϕ |
Sdt , |
(20.14) |
|
|
dx |
|