
Физика [РТФ, Браже & Долгов, 1 семестр] / Шизика
.pdf
Используя (10.1), найдем частные производные смещения u по времени и координатам:
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
∂u |
= −ωAsin (ωt −kr ); |
∂ |
|
u2 = −ω2 Acos(ωt −kr )= −ω2u; |
|||||||||||||
∂t |
|
|
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂u |
|
|
∂ |
2 |
u2 = −kx2 Acos |
|
|
|
|
|
||||||
|
= kx sin (ωt −kr ); |
(ωt −kr )= −kx2u; |
|||||||||||||||
|
|
||||||||||||||||
|
∂x |
|
|
∂x |
|
|
|
|
|
|
|
|
|||||
|
|
∂2u |
= −k |
2 |
u; |
∂2u |
= −k |
2 |
u. |
|
|
|
|||||
|
|
∂y2 |
y |
∂z2 |
z |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Вводя оператор Лапласа ∆ = ∂2 |
∂ x2 +∂2 |
|
∂y2 +∂2 ∂z2 , записан- |
||||||||||||||
ные выражения можно свести к виду |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
2 |
u2 , |
|
|
u = −(kx2 + ky2 + kz2 )u = −k |
2u = −ω2 |
u = |
∂ |
||||||||||||
|
|
2 |
∂t |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
v |
|
|
|
|
|
∆u = |
1 ∂2u |
. |
|
|
|
|
|
(10.4) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
v2 ∂t2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение (10.4) называется волновым уравнением для плоских упругих волн в однородной, изотропной среде.
§ 2. Электромагнитные волны
Если в упругих волнах колеблются частицы среды, то в электромагнитных волнах колеблются электрическое и магнитное поля. Следовательно, в отличие от упругих волн, электромагнитные волны могут распространяться даже в вакууме.
Рассмотрим для простоты случай однородной, изотропной среды, когда относительные диэлектрическая и магнитная проницаемо-
121
сти являются постоянными величинами (ε, µ = const). Будем предполагать также, что среда не заряжена (т. е объемная плотность заряда ρ = 0 ) и не проводит электрический ток (т. е. удельная электропроводность среды σ = 0). Частным случаем такой среды является ваку-
ум (ε, µ =1).
Из уравнений Максвелла (см. лекцию 4) для рассматриваемой среды после довольно громоздких преобразований, которые мы здесь опускаем, можно получить следующие два уравнения, описывающие распространение в ней электромагнитных волн:
|
1 ∂2 E |
|
|
|
|
|
|
1 ∂2 H |
|
|
|||||||||||||
∆E = |
|
|
|
|
|
|
|
|
, |
|
∆H = |
|
|
|
|
|
|
, |
(10.5) |
||||
v2 |
|
∂t2 |
|
v2 |
|
∂t2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v = |
|
1 |
|
|
|
|
1 |
|
|
= |
|
c |
|
= |
c |
. |
|
(10.6) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ε |
0 |
µ |
0 |
|
|
|
εµ |
|
|
|
εµ |
|
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
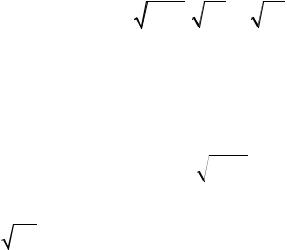
Здесь v обозначает скорость распространения электромагнитных волн в среде с относительными диэлектрической и магнитной проницаемостями ε и µ , c =1/ 
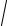 ε0µ0 – скорость распространения электромагнитных волн в вакууме (электродинамическая постоянная), а n =
ε0µ0 – скорость распространения электромагнитных волн в вакууме (электродинамическая постоянная), а n = 
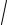 εµ – показатель преломления среды, показывающий, во сколько раз уменьшается скорость волны в данной среде по сравнению с вакуумом.
εµ – показатель преломления среды, показывающий, во сколько раз уменьшается скорость волны в данной среде по сравнению с вакуумом.
Решения уравнений (10.5) для плоских электромагнитных волн, бегущих вдоль оси x в рассматриваемой нами среде, имеют вид, математически эквивалентный выражению (10.2), являющемуся решением аналогичного уравнения (10.4):
122

E = Em cos(ωt ± kx), H = Hm cos(ωt ± kx), |
(10.7) |
где Em и Hm – соответственно амплитуды колебаний напряженности электрического и магнитного полей, а знаки «плюс» и «минус» соответственно относятся к волнам, бегущим вдоль отрицательного и положительного направлений оси x. Электрическое поле здесь обусловлено изменением во времени магнитного поля, а магнитное поле, в свою очередь, обусловлено изменением во времени электрического поля. Оба поля вихревые, поэтому их силовые линии перпендикулярны друг другу. График такой волны представлен на рис. 10.3.
y |
v |
Em |
0 |
x |
Hm
z
Рис. 10.3. График плоской бегущей электромагнитной волны в неограниченной,
однородной, изотропной, незаряженной диэлектрической среде
§ 3. Энергия бегущей волны
Пусть за время dt через площадку площадью S , перпендикулярную направлению распространения бегущей волны любой природы, будет перенесена энергия dE , запасенная в объеме dV цилиндра с площадью оcнования dS и длиной vdt (рис. 10.4). Если w = dE / dV – объемная плотность энергии в волне, то dE = wvS dt .
123

v
vdt
Рис. 10.4. К выводу выражения для вектора плотности потока энергии волны
Потоком энергии волны называется физическая величина, равная энергии, переносимой волной в единицу времени через некоторую площадку, перпендикулярную направлению распространения волны:
Φ = dEdt .
Плотностью потока энергии волны называется физиче-
ская величина, равная потоку ее энергии через перпендикулярную к направлению распространения волны площадку единичной площади:
S = Φ = 1 dE = wv.
S S dt
Поскольку скорость распространения волны v является векторной величиной, то имеет смысл ввести вектор плотности потока энергии
S = wv. |
(10.8) |
124

Понятие о потоке энергии бегущей волны было впервые введено русским физиком Н. А. Умовым (уроженцем г. Симбирска) в 1874 г. Вектор плотности потока энергии применительно к электромагнитным волнам ввел в 1884 г. английский физик Дж. Пойнтинг.
Интенсивностью волны называется среднее по времени значение плотности потока энергии бегущей волны:
I =  S
S 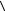 =
= 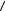 w
w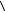 v.
v.
Упругие волны. Средняя плотность энергии в упругой волне может быть найдена как энергия гармонических колебаний элемента упругой среды единичного объема:
|
dE |
|
(1/ 2)ρdVω2 A2 |
|
1 |
|
2 2 |
w = |
dV |
= |
dV |
= |
2 |
ρω |
A , |
где ρ – средняя плотность среды, ω и А – соответственно частота и амплитуда волны. Отсюда, согласно определению, интенсивность упругой волны
I = |
1 |
ρω2 A2v. |
(10.9) |
|
2 |
|
|
Электромагнитные волны. Объемная плотность энергии электромагнитного поля складывается из соответствующих слагаемых для электрической и магнитной составляющих этого поля:
w = 12 (ε0εE2 + µ0 µH 2 ).
125

В рассматриваемой нами однородной, изотропной, незаряженной и непроводящей среде оба этих слагаемых равны по величине, откуда 
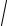 ε0ε E =
ε0ε E = 
 µ0µH и, согласно (10.5),
µ0µH и, согласно (10.5),
w= 
 ε0εµ0µEH = EH
ε0εµ0µEH = EH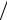 v.
v.
Всоответствии с (10.8) вектор Пойнтинга S = EHv / v или
|
|
(10.10) |
S = EH . |
||
Тогда интенсивность электромагнитной волны
|
|
S |
|
|
|
|
|
|
1 |
|
|
|
|
|
I = |
|
|
= ε εE2v = |
ε0ε |
|
E2 = |
ε0ε |
|
E2 |
, |
(10.11) |
|||
|
|
|||||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
µ0µ |
|
|
2 |
µ0µ |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
так как среднее значение квадрата косинуса равно 1/2. Здесь имеется в виду усреднение за время, превышающее период колебаний.
Обратите внимание: интенсивность как упругих, так и электромагнитных волн пропорциональна квадрату амплитуды, однако, в отличие от упругих волн, в случае электромагнитных волн она не зависит от часто-
ты колебаний. Дело здесь в том, что ρω2 – это коэффициент упругости
единичного объема колеблющейся среды, определяющий объемную плотность энергии в упругих волнах. Влияние среды на объемную плотность энергии в электромагнитных волнах проявляется через значения ее относительных диэлектрической и магнитной проницаемостей.
§ 4. Скорости распространения упругих волн
Прежде всего, отметим, что распространение упругих волн в твердых телах существенно отличается от их распространения в жидкостях и газах. В твердых телах упругими являются как продольные
126
деформации растяжения-сжатия, так и поперечные деформации сдвига. Поэтому в изотропных твердых телах могут распространяться как продольные волны, в которых частицы среды колеблются в направлении распространения волны, так и поперечные волны, в которых частицы колеблются перпендикулярно этому направлению. В кристаллах наличие анизотропии упругих свойств приводит к тому, что чисто продольные и чисто поперечные упругие волны могут распространяться лишь в направлениях так называемых акустических нормалей, а в прочих направлениях распространяются квазипродольные и квазипоперечные упругие волны.
В жидкостях и газах сдвиговые деформации не являются упругими. По этой причине в них могут распространяться лишь продольные упругие волны. Разумеется, здесь мы имеем в виду лишь обычные, не слишком вязкие жидкости.
Твердые тела. Пусть вследствие распространения упругой волны в некотором стержне с площадью поперечного сечения S за время dt деформируется масса dm = ρSvdt, где ρ – плотность материала стержня, v – скорость распространения волны. Уравнение движения
деформируемой части стержня имеет вид |
|
|||||
|
d (mx) |
= |
dm |
x |
= F =σS, |
(10.12) |
|
dt |
dt |
||||
|
|
|
|
|
||
где x – колебательная скорость частиц среды в области деформации (в силу малости величины dm ее можно считать одинаковой для всех частиц и не зависящей от времени в течение деформации), F – сила упругой деформации и σ – упругое напряжение в среде.
Согласно закону Гука, для деформаций растяжения-сжатия σ = Eε , а для деформаций сдвига σ = Gε , где E – модуль Юнга, G –
127

модуль сдвига, а ε = l / l – относительная деформация. Тогда уравнение (10.12) можно переписать в виде
ρvx = Eε |
(10.13) |
для продольных волн или в виде
ρvx = Gε |
(10.14) |
для сдвиговых волн.
Поскольку l = xt , а l = vt , то из (1 0.13), (10.14) получаем выражения для скоростей распространения продольных и поперечных упругих волн в стержне:
vL = |
|
E |
|
, |
(10.15) |
||
ρ |
|||||||
|
|
|
|
|
|
||
|
|
. |
|
||||
v = |
G |
(10.16) |
|||||
T |
ρ |
|
|
|
|
||
|
|
|
|
|
|
||
Здесь для скоростей распространения продольных (longitudinal – англ.) и поперечных (transverse – англ.) волн введены соответственно обозначения vL и vT .
Газы. В случае газов в (10.15) можно подставить выражение для плотности среды, полученное из уравнения Клапейрона – Менделеева: ρ = µ p / (RT ), где p – давление газа в области деформации. Оно совпадает с упругим напряжением: p =σ = Eε ≈ E , поскольку газы обладают хорошей сжимаемостью (ε ≈1). Тогда для скорости распространения упругих волн в газах получаем
v = |
RT |
. |
(10.17) |
|
µ |
|
|
128

Снова воспользовавшись уравнением Клапейрона – Менделеева, можно переписать (10.17) в виде
v = |
|
p |
|
. |
(10.18) |
|
|||||
|
|
ρ |
|
||
Следует отметить, что и температура Т в (10.17), и давление p , и плотность газа ρ в (10.18) соответствуют своим значениям в области сжатия (разрежения). Считая, что процесс распространения упругих волн в газе является изотермическим (T = const) и используя закон Бойля – Мариотта
pV = mµ RT = const
в виде
ρp = RTµ = const,
Ньютон записал выражение для скорости упругих волн (10.18) в виде
vN = |
|
p0 |
|
, |
(10.19) |
|
ρ0 |
||||||
|
|
|
|
|
где p0 и ρ0 – соответственно равновесные значения давления и плотности газа. Применительно к упругим волнам звукового диапазона формула (10.19) определят так называемую ньютоновскую или изо-
термическую скорость звука.
Она дает заниженный результат по сравнению с экспериментально найденными значениями скорости звука в газах, так как в действительности процесс распространения упругих волн в них, как правило, не является изотермическим. Тепловой поток не успевает вы-
129

ровнять температуры в областях сжатия и разрежения. Более строгое рассмотрение вопроса о скорости звука в условиях адиабатического распространения (без теплообмена) приводит к формуле
v = |
γ |
p0 |
|
, |
(10.20) |
|
ρ0 |
||||||
|
|
|
|
|
где γ – показатель адиабаты, равный отношению теплоемкостей газа при постоянном давлении и постоянном объеме.
Заметим, однако, что формула (10.19) дает правильный результат в случае весьма коротких упругих волн, когда длина свободного пробега молекул газа оказывается больше половины длины волны. Тогда, не успевая столкнуться друг с другом, молекулы могут переносить тепло из области сжатия в область разрежения и выравнивать температуру газа.
Жидкости. Свойства жидкостей сочетают в себе свойства твердых тел и газов. Их сжимаемость хуже, чем у газов, но выше, чем у твердых тел.
Сжимаемостью называется физическая величина, равная отношению относительного уменьшения объема тела к вызвавшему его увеличению давления:
β = − ∆1p ∆VV .
Сжимаемость, соответствующая условиям адиабатического процесса, называется адиабатической сжимаемостью. Величина, обратная сжимаемости, называется модулем объемной упругости. Тогда по аналогии с формулами (10.15), (10.16), с учетом сказанного выше относительно трудностей выравнивания температуры в облас-
130
