Физика [РТФ, Браже & Долгов, 1 семестр] / Шизика

чала системы S′, проведенный из начала системы S , которую мы условно считаем неподвижной.

Рис. 1.1. К выводу преобразований Галилея

Разложим обозначенные на рис. 1.1 радиус-векторы по координатам:

r′ = ix′+ jy′+ k′, r = ix + jy + kz, r0 = ix0 + iVt,

Формулы (1.4) носят название преобразований Галилея. Естественно, если скорость переноса V системы S′ относительно системы S имеет другое направление, то выражения (1.4) имеют иной вид.

21

Обратите внимание: одинаковость хода времени в обеих рассматриваемых ИСО не следует из рис. 1.1. Этот факт постулируется нами, исходя из нашего повседневного опыта. Нам кажется логичным, что часы, отсчитывающие время в данной аудитории, показывают такое же время, как и часы наблюдателя, проезжающего на автомобиле мимо университета (при условии, что и те, и другие часы были предварительно сверены по сигналам точного времени).

Пусть, например, мы наблюдаем некоторое тело в виде длинного тонкого стержня, лежащего на оси x в системе S. Его длина, равная разности координат конца x2 и начала x1, может быть найдена как

L = x2 − x1 .

Из (1.4) следует, что длина этого же тела, измеренная наблюдателем, находящимся в системе S′, равна

L′ = x2′ − x1′ = (x2 −Vt2 ) −(x1 −Vt1).

Поскольку измерения координат конца и начала стержня должны проводиться одновременно, то t2 = t1 и L′ = x2 − x1 = L .

Аналогично, из (1.4) следует, что длительность какого-либо события, измеренная по часам наблюдателя, находящегося в системе S,

τ = t2 −t1

равна длительности этого же события, измеренной по часам наблюдателя, находящегося в системе S′:

τ′ = t2′ −t1′ = t2 −t1 =τ.

22

Величины, остающиеся неизменными при каких-либо преобразованиях, например, не зависящие от выбора системы отсчета, называются инвариантами (от лат. invarians – неизменяющийся). Таким образом, в классической механике имеется два инварианта: длина тела и длительность события.

§3. Законы Ньютона

Воснове классической механики лежат три закона динамики, сформулированные Ньютоном в 1687 г. Они ниоткуда не выводятся, а являются обобщением результатов наблюдения за движением и взаимодействием тел в природе, т. е. постулатами теории. Приведем эти законы в современной формулировке.

Первый закон Ньютона

Если на тело не действуют никакие силы или их равнодействующая равна нулю, то оно сохраняет состояние покоя или прямолинейного равномерного движения.

На языке математики это выглядит так:

∑Fi = 0 a = 0.

i

Второй закон Ньютона

Производная импульса тела по времени равна результирующей силе, действующей на это тело.

Математически это можно записать в следующем виде:

23

(m = const), принимая во внимание (1.2), (1.3), получаем известную из школьного курса физики форму записи второго закона Ньютона: ma = F.

Третий закон Ньютона

При взаимодействии двух тел сила, с которой первое тело действует на второе, равна по величине и противоположна по направлению силе, с которой второе тело действует на первое.

В математической записи это выглядит так:

Законы Ньютоны выполняются лишь в ИСО. Поскольку это математическая абстракция, то применение законов Ньютона к реальным системам отсчета приводит к погрешностям, связанным с действием в них сил инерции. В ряде случаев это обстоятельство необходимо учитывать.

§ 4. Сложение скоростей

Вернемся к рис. 1.1 и допустим, что система S′ участвует как в поступательном (с постоянной скоростью V ), так и во вращательном (с постоянной угловой скоростью ω ) движении относительно ИСО S. Таким образом, в общем случае система S′может быть НИСО. Тогда

24

выполняется следующий закон нахождения скорости материальной точки P в неподвижной ИСО S:

где vабс = dr / dt − ее абсолютная скорость, vотн = dr′/ dt − относи-

тельная скорость, т. е. скорость движения относительно системы S′, vпост =V − скорость поступательного движения НИСО относительно ИСО, а vвр = [ωr′] − скорость вращения материальной точки относи-

тельно оси, проходящей через начало системы координат, связанной с НИСО.

Ради простоты изложения мы опустили здесь подробности вывода выражения (1.7), однако последнее слагаемое в нем требует некоторых пояснений, так как содержит векторное произведение векторов ω и r′.

тройку векторов, модуль которого c = a b sinα (см. рисунок).

Правовинтовая тройка векторов соответствует правилу буравчика или

штопора: если рукоятку штопора поворачивать в направлении от

первого вектора ко второму по наиболее короткому расстоянию, то направление его ввинчивания указывает, как направлен вектор векторного произведения данных векторов.

c

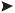α b

a

25

§ 5. Сложение ускорений

Чтобы найти абсолютное ускорение материальной точки, продифференцируем по времени выражение (1.7). Вновь опуская подробности вывода, можно получить следующее выражение:

званное так в честь французского физика Г. Кориолиса (1792–1843), занимавшегося изучением влияния вращения системы отсчета на относительное движение материальной точи, и aцб = − ω[ωr′] − цен-

тробежное ускорение. Вам оно больше известно в виде, приводимом в школьных учебниках физики: aцб =ω2r или aцб = v2 / r . Приведенное здесь векторное выражение является более общим, так как определяет не только численное значение центробежного ускорения, но и его направление.

§ 6. Центр масс

Под центром масс (центром инерции) системы материаль-

ных точек понимают точку, радиус-вектор которой

где mi и ri – соответственно масса и радиус-вектор i-й материальной точки, а m – масса всей системы.

26

Обратите внимание: понятие центра масс не тождественно понятию центра тяжести. Последний имеет смысл только для твердого тела, находящегося в однородном поле тяжести.

Умножим на массу всей системы производную по времени ра- диус-вектора ее центра масс:

т. е.

mvC = P,

где vC – скорость движения центра масс, а P – полный импульс системы.

Продифференцируем теперь полученное выражение по времени:

где a C – ускорение, с которым движется центр масс системы. С другой стороны,

где верхние индексы в круглых скобках относятся соответственно к внутренним (англ. internal) и внешним (англ. external) силам, действующим на i-ю материальную точку. Суммируя внутренние и внешние силы по отдельности, можем записать

27

Первая сумма представляет собой сумму сил парных взаимодействий всех материальных точек, образующих систему, между собой. Она равна нулю по третьему закону Ньютона. Вторая сумма равна результирующей всех внешних сил, действующих на систему. Объеди-

няя (1.9), (1.10), получаем

Выражение (1.11) является записью теоремы о движении цен-

тра масс системы:

Центр масс системы движется так, как двигалась бы материальная точка с массой, равной массе всей системы, под действием всех внешних сил, приложенных к данной системе.

§ 7. Поступательное движение твердого тела

Рассмотрим наиболее простой случай системы материальных точек – так называемое абсолютно твердое тело.

Под абсолютно твердым телом в механике понимают такое тело, взаимное расположение точек которого не изменяется со временем, а также в процессе движения.

Модель абсолютно твердого тела позволяет решать большой круг задач, связанных с движением реальных тел. В дальнейшем, говоря о твердом теле, мы будем иметь в виду именно такое тело.

28

При поступательном движении твердого тела все его точки в любой момент времени будут двигаться параллельно друг другу с одинаковой скоростью vi = vC и с одинаковым ускорением ai = aC .

Отсюда следует, что поступательное движение твердого тела однозначно характеризуется движением его центра масс и подчиняется теореме о движении центра масс системы (1.11).

В частности, если на твердое тело не действует никакая сила или их равнодействующая равна нулю (F (e) = 0), то оно сохраняет состояние покоя или прямолинейного равномерного движения.

§ 8. Вращательное движение твердого тела

Вращение материальной точки. Рассмотрим вращение твердо-

го тела вокруг неподвижной оси z, проходящей через его центр инерции О. Вначале, для удобства, проанализируем характеристики вращения произвольной материальной точки массой mi из массива этого тела, имеющей радиус-вектор ri (рис. 1.2). В общем случае это вращение ускоренное и происходит за счет действия силы Fi = mia со скоростью vi .

vi

Рис. 1.2. Вращение материальной точки вокруг неподвижной оси

29

Определим угловую скорость материальной точки как угол ее поворота в единицу времени:

где k − единичный вектор направления оси z.

Угловая скорость – векторная величина. Ее направление определяется правилом буравчика (см. выше): если рукоятку буравчика поворачивать в направлении вращения материальной точки, то направление его ввинчивания указывает направление вектора угловой скорости.

Обратите внимание: в отличие от вектора линейной скорости, вектор угловой скорости направлен не в сторону движения материальной точки, а вдоль оси ее вращения. В связи с этим отметим, что векторы делятся на полярные (обычные) и аксиальные (псевдовекторы). Первые не связаны с вращением, а вторые описывают вращение вокруг некоторой оси. Вектор угловой скорости является аксиальным вектором.

Угловое ускорение материальной точки рассматривается как быстрота изменения ее угловой скорости или, с математической точки зрения, как векторная величина, равная производной по времени ее угловой скорости:

(dω > 0), то вектор углового ускорения сонаправлен с вектором угловой скорости: ε ↑↑ω. Если вращение замедляется (dω < 0) , то н а-

30