
- •ВВЕДЕНИЕ
- •1. ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ ТВЕРДОГО ТЕЛА
- •1.1. Основные понятия и определения
- •1.2. Аксиомы статики
- •1.3. Основные типы реакций связей
- •1.3.1. Свободное опирание тела о связь
- •1.3.3. Стержневая связь
- •1.3.4. Шарнирно-подвижная опора
- •1.3.5. Шарнирно-неподвижная опора
- •1.4. Система сходящихся сил
- •1.5. Момент силы относительно точки и оси
- •2. ПЛОСКАЯ СИСТЕМА СИЛ
- •2.1. Различные формы условий равновесия плоской системы сил
- •2.2. Центр параллельных сил
- •3. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- •3.1. Способы задания движения точки
- •3.1.1. Естественный способ задания движения точки
- •3.1.2. Координатный способ задания движения точки
- •3.2. Простейшие движения твердого тела
- •3.2.1. Поступательное движение
- •3.2.2. Вращательное движение
- •4. СЛОЖНОЕ ДВИЖЕНИЕ
- •4.1. Сложное движение точки
- •4.1.1. Относительное, переносное и абсолютное движение
- •4.1.2. Теорема о скорости точки в сложном движении
- •4.1.3. Плоскопараллельное движение твердого тела
- •4.1.4. Разложение плоскопараллельного движения на поступательное и вращательное
- •4.1.5. Скорость точки плоской фигуры
- •5. ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- •5.1. Основные положения динамики. Аксиомы динамики
- •5.2. Дифференциальные уравнения движения материальной точки
- •5.3. Две основные задачи динамики точки
- •6. ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
- •6.1. Динамические дифференциальные уравнения относительного движения материальной точки
- •6.2. Частные случаи динамической теоремы Кориолиса
- •7. ДИНАМИКА ТВЕРДОГО ТЕЛА
- •7.1. Понятие о механической системе
- •7.2. Принцип Даламбера
- •7.3. Уравнение динамики вращающегося тела
- •7.4. Моменты инерции простейших однородных тел
- •8. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
- •8.1. Обобщенные координаты
- •8.2. Возможные перемещения
- •8.3. Принцип возможных перемещений
- •9. ОСНОВЫ ТЕОРИИ КОЛЕБАНИЙ, ТЕОРИИ УДАРА
- •9.1. Устойчивость положения равновесия
- •9.2. Колебания системы с одной степенью свободы
- •9.3. Общие положения теории удара
- •10. ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
- •10.1. Основные допущения
- •10.2. Напряжения
- •10.3. Перемещения и деформации. Закон Гука
- •11. Растяжение и сжатие
- •11.1. Диаграмма растяжения
- •11.2. Методы расчета строительных конструкций
- •12. Геометрические характеристики плоских сечений
- •12.1. Моменты инерции сечения
- •12.2. Момент инерции при параллельном переносе осей
- •13. ИЗГИБ И КРУЧЕНИЕ СТЕРЖНЕЙ
- •13.1. Расчеты на прочность при кручении стержней. Крутящий момент. Построение эпюр
- •13.2. Расчеты на прочность при изгибе стержней
- •14. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
- •14.1. Основные понятия
- •14.2. Формула Эйлера для критической силы
- •14.3. Влияние способа закрепления концов стержня на значение критической силы
- •14.4. Практический расчет сжатых стержней
- •15. ТЕОРИЯ ТОНКИХ ПЛАСТИН
- •15.1. Основные понятия и гипотезы
- •15.2. Соотношения между деформациями и перемещениями
- •15.3. Напряжения и усилия в пластинке
- •15.4. Усилия в пластинке
- •15.5. Дифференциальное уравнение изогнутой поверхности пластинки
- •16. Динамическое нагружение
- •16.1. Динамические расчеты элементов конструкций. Ударная нагрузка, коэффициент динамичности
- •16.2. Вычисление напряжений при равноускоренном движении
- •16.3. Определение перемещений и напряжений при ударе
- •16.4. Частные случаи
- •17. ПРОЧНОСТЬ МАТЕРИАЛОВ ПРИ ЦИКЛИЧЕСКИ МЕНЯЮЩИХСЯ НАПРЯЖЕНИЯХ
- •17.1. Усталостное разрушение материала
- •17.2. Характеристики циклов напряжений
- •17.3. Предел выносливости
- •17.4. Факторы, влияющие на усталостную прочность материала
- •18. ПРОБЛЕМЫ ТЕОРИИ МЕХАНИЗМОВ И МАШИН
- •18.1. Классификация кинематических пар
- •18.2. Структура и кинематика плоских механизмов
- •18.3. Структурная формула кинематической цепи общего вида
- •18.4. Структурная формула плоских механизмов
- •18.5. Пассивные связи и лишние степени свободы
- •18.6. Замена в плоских механизмах высших кинематических пар низшими
- •18.7. Классификация плоских механизмов
- •18.8. Структурные группы пространственных механизмов
- •19. Анализ механизмов
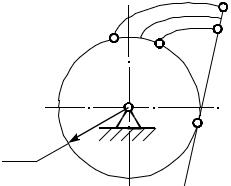
- •19.1. Кинематический анализ механизмов
- •19.1.1. Графическое определение положений звеньев механизма и построение траектории
- •19.1.2. Определение скоростей и ускорений точек звеньев методом планов
- •19.1.3. Свойство планов скоростей
- •19.1.4. Свойства плана ускорений
- •19.1.5. Построение плана скоростей и ускорений кулисного механизма (рис. 19.5)
- •19.2. Силовой анализ механизмов
- •19.2.1. Условие статической определимости кинематических цепей
- •19.2.2. Силы, действующие на звенья механизма
- •19.2.3. Силы инерции звена, совершающего возвратно-поступательное движение
- •19.2.4. Силы инерции звена, совершающего вращательное движение вокруг неподвижной оси
- •19.2.5. Силы инерции звена, совершающего плоское движение (рис. 19.14)
- •19.3.1. Силовой расчет начального звена (рис. 19.15, а)
- •20. Общие сведения о проектировании машин
- •20.1. Стадии проектирования
- •20.2. Основные термины и определения
- •21. Передачи. общие вопросы
- •21.1. Назначение и классификация передач
- •21.2. Классификация передач
- •21.3. Основные кинематические характеристики передач
- •21.4. Передачи с постоянным передаточным числом
- •21.5. Передачи с переменным передаточным числом
- •22. Зубчатые передачи
- •22.1. Общие сведения
- •22.2. Механизмы с высшими парами
- •22.2.1. Зубчатые передачи
- •22.2.2. Геометрические элементы зубчатых колес
- •22.3. Зубчатые механизмы с подвижными осями
- •22.4. Расчет основных геометрических параметров цилиндрических прямозубых колес
- •22.5. Расчет основных геометрических параметров конических прямозубых колес
- •23. Зубчатые редукторы. Общие сведения
- •23.1. Классификация редукторов
- •23.2. Принципиальная конструкция цилиндрического редуктора
- •23.3. Расчет основных конструктивных параметров редукторов
- •24. Ременные передачи
- •24.1. Общие сведения
- •24.1.1. Классификация
- •24.2. Кинематические и силовые зависимости
- •24.2.1. Напряжения в ремне
- •24.2.2. Относительное скольжение ремня
- •25. Цепные передачи
- •25.1. Общие вопросы
- •25.2. Классификация цепных передач
- •25.3. Достоинства и недостатки цепных передач
- •25.4. Детали цепных передач
- •25.5. Основные параметры цепных передач
- •26. ОСИ И ВАЛЫ
- •26.1. Общие сведения
- •26.2. Проектный расчет валов и осей
- •26.2.1. Составление расчетных схем
- •26.2.2. Расчёт опасного сечения
- •26.3. Проверочные расчеты валов и осей
- •26.3.1. Расчет на выносливость валов и осей
- •26.3.2. Расчет валов и неподвижных осей на статическую прочность
- •26.4. Проверочный расчет валов и осей на жесткость
- •27. ПОДШИПНИКИ, МУФТЫ
- •27.1. Подшипники
- •27.1.1. Подшипники скольжения
- •27.1.2. Подшипники качения
- •27.2. Муфты
- •27.2.1. Волновые передачи
- •заключение
- •Библиографический список
8) возможность использования широкой номенклатуры материалов.
Недостатки передач:
1)сложность изготовления;
2)наличие шума во время работы;
3)не предохраняют детали машины от поломок во время перегрузок.
Зубчатая передача состоит из 2-х колес, имеющих чередующие зубья и впадины. Меньшее из двух сцепляющихся колес называется шестерней, а большее – колесом. Параметры шестер-
ни сопровождаются индексом “1”, а колеса– “2”. Наиболее распространенными являются передачи с эвольвентным профилем зуба. Эвольвентное зацепление обладает технологическими достоинствами. Зубчатые передачи находят широкое применение в различных отраслях промышленности: автотракторостроении, станкостроении, самолетостроении, энергетическом машиностроении и др. для передачи усилий от весьма малых значений до 100 000 кВт. Размеры зубчатого колеса могут быть от нескольких миллиметров до нескольких метров (12 м и более).
22.2. Механизмы с высшими парами
22.2.1. Зубчатые передачи
Для того чтобы исключить проскальзывание и увеличить передаваемую мощность, используют зубчатые передачи. Они очень широко применяются в технике, их изучает наука, называемая теорией зубчатого зацепления.
Для того чтобы передаточное отношение было постоянным, необходимо, чтобы профили зубьев удовлетворяли некоторым условиям.
Пусть два звена, вращающиеся вокруг осей О1 и О2, образуют в точкеК высшую кинематическую пару (рис. 22.1).
Очевидно, что относительная скорость должна лежать на ка-
сательной τ-τ к сопряженным профилям, т.к. в противном случае нормальная составляющая относительной скорости привела бы
154
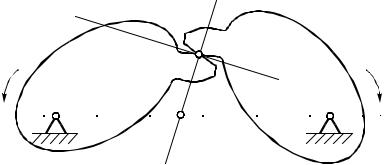
либо к отрыву звеньев друг от друга, либо к внедрению одного звена в другое. Из этого следует, что мгновенный центр скоростей в относительном движении лежит на нормалиn-n, проведенной в точке контакта к сопряженным профилям. В то же время мгновенный центр скоростей должен лежать на прямойО1О2, соединяющей оси вращения звеньев 1 и 2. Следовательно, мгновенным центром скоростей в относительном движении является точка Р, лежащая на пересечении нормалиn-n и линии О1О2. В теории зубчатого зацепления эту точку называютполюсом зацепления.
|
|
|
|
|
τ |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
. |
|
|||||||
q. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
||
|
|
|
|
|
|
|
|
|
|
|
|
τ |
||||||||
|
|
|
O |
|
|
|
|
|
|
|
|
|
O2 |
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
||
n
Рис. 22.1
Из определения мгновенного центра скоростей следует, что относительная скорость в точке Р равна нулю, т.е.
VP1 = VP2.
Следовательно,
q O1P = ϕ O2 P . |
(22.1) |
|
|
|
|
Отсюда передаточное отношение i12:
|
|
|
|
|
|
i |
= |
q |
= O2 P . |
(22.2) |
|
|
|||||
12 |
|
O1P |
|
||
|
|
ϕ |
|
Иными словами, нормаль, проведенная в точке контакта к сопряженным профилям, делит межосевое расстояние в отношении, обратно пропорциональном отношению угловых скоро-
стей. Это – основная теорема зацепления. Для того чтобы пере-
155
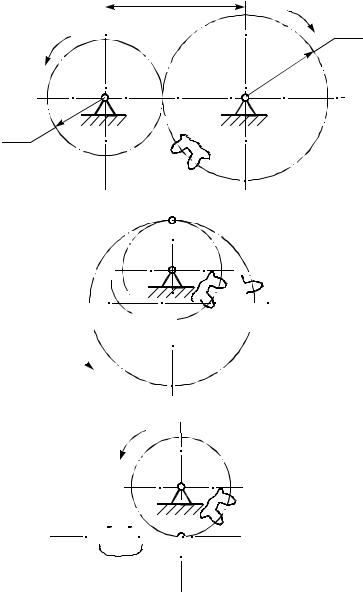
даточное отношение i12 было постоянным, необходимо, чтобы полюс зацепления занимал постоянное положение. В этом случае центроидами в относительном движении будут являться окружности, которые в теории зубчатого зацепления называются начальными окружностями. Все размеры, относящиеся к начальным окружностям, помечают индексомw, например: rw1, rw2
– радиусы начальных окружностей (рис. 22.2, а).
Радиусу начальной окружности rw пропорциональна длина начальной окружности и, следовательно, число зубьев z, которое может на ней разместиться. Поэтому для передаточного отношения справедливо выражение
|
|
|
|
|
|
|
i |
= |
q |
= − |
z2 |
. |
(22.3) |
|
|
|||||
12 |
|
|
z1 |
|
||
|
|
ϕ |
|
|
||
Знак «минус», стоящий перед отношением чисел зубьев ведомого и ведущего колеса, показывает, что в передачевнешнего зацепления ведущее и ведомое колеса вращаются в противоположные стороны, а передаточное отношение –отрицательное.
Расстояние между осями вращения зубчатых колес называют межосевым расстоянием и обозначают аw. В случае внешнего зацепления
аw = rw1 + rw2. |
(22.4) |
Учитывая, что rw1 = O1P, rw2 = O2P, из (22.2) и (22.4) получим
r |
= |
|
aw |
|
,r |
= |
awi12 |
. |
(22.5) |
|
|
|
|
||||||||
w1 |
|
i |
|
+1 |
w2 |
|
i +1 |
|
||
|
|
12 |
|
|
|
|
12 |
|
|
|
Для того чтобы уменьшить габариты передачи, используют колеса внутреннего зацепления: одно колесо вставляется внутрь другого (рис. 22.2, б). В этом случае направление вращения ведущего и ведомого колес совпадает, поэтому передаточное отношение – положительное:
|
|
|
|
z2 |
|
|
i |
= |
q |
= |
. |
(22.6) |
|
|
|
|||||
12 |
|
|
z1 |
|
||
|
|
ϕ |
|
|
||
|
|
|
156 |
|
||
a |
w |
. |
q. |
ϕ |
|
|
rw2 |
O1 |
O2 |
rw1 |
|
a
 P
P
O1
ϕ. 
 q.
q. 

 O2
O2

q. б
O1
_ 


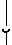 P V
P V
Q
в
Рис. 22.2
157
Межосевое расстояние равно разности радиусов начальных окружностей:
аw = rw2 – rw1.
Тогда радиусы начальных окружностей равны
r |
= |
aw |
, |
r |
= |
awi12 |
. |
|
|
||||||
w1 |
|
i12 −1 |
w2 |
|
i12 −1 |
||
|
|
|
|
||||
(22.7)
(22.8)
Если rw2 → ∞, то начальная окружность превращается в начальную прямую, а зубчатое колесо – в зубчатую рейку. В
этом случае получают зубчато-реечную передачу (рис. 22.2, в).
Поскольку в полюсе зацепления относительная скорость равна 0, то VP1 = VP2, тогда
|
|
|
|
1 |
|
|
i |
= |
q |
= |
. |
(22.9) |
|
|
|
|||||
12 |
V |
|
r1 |
|
||
|
|
|
||||
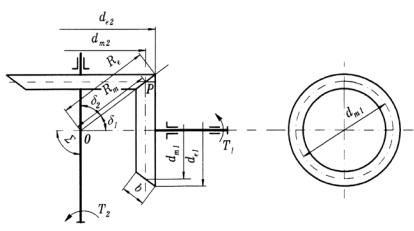
Для передачи вращения между валами с пересекающимися осями используют конические колеса (рис. 22.3). Чаще всего
угол между осями δ1 + δ2 = 900 (такие передачи называют ортогональными), но возможны и другие углы.
Рис. 22.3
158
В передачах с коническими колесами существует мгновенная ось (OP) – геометрическое место точек тел, имеющих в данный момент нулевую относительную скорость. Если мгновенную ось ОР, наклоненную к оси вращения шестерни под
углом δ1, вращать вокруг оси 1, получится коническая поверхность – подвижная аксоида (поверхность, образованная мгновенной осью в локальной системе координат, связанной со звеном 1 или 2, называют подвижной аксоидой). Аналогично при вращении мгновенной оси ОР вокруг оси 2 получим кониче-
скую поверхность с половиной угла при вершине равной δ2 (вторая подвижная аксоида). Подвижные аксоиды в теории зубчатых зацеплений называются начальными конусами. Зубья колес располагают вблизи начальных конусов, а поверхности вершин и впадин имеют ту же форму, что и начальные конусы.
В качестве главного профиля зубьев цилиндрических зубчатых колес, применяемых в машиностроении, наибольшее распространение получил эвольвентный профиль. Плоская эвольвента окружности представляет собой траекторию любой точки прямой линии, перекатываемой без скольжения по эволюте, т.е. по основной окружности радиуса rb (рис. 22.4).
Прямая линия, перекатываемая по основной окружности,
называется производящей прямой.
q. K |
K |
0 |
D |
O |
D0 |
|
|
rb |
C |
|
Рис. 22.4
159
