5) долговечность и значимость проектируемого сооружения или машины.
Величины допускаемых напряжений или коэффициентов запаса прочности устанавливаются нормами проектирования и техническими условиями. Для строительных сталей коэффициента запаса прочности принимается n = 1,4…1,6; для хрупких материалов n = 2,5…3,5; для древесины n = 3,5…6.
12. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
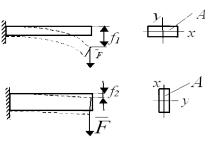
При расчетах на прочность конструкций используются различные геометрические характеристики. Так, например, при растяжении – сжатии использовалась площадь поперечного сечения стержня. Однако при других деформациях эта геометрическая характеристика не является достаточной. При изгибе стержня прямоугольного сечения существенным является направление плоскости действия силы по отношению к ориентации осей симметрии сечения (рис. 12.1).
Рис. 12.1
Следовательно, при одной и той же площади поперечного сечения стержня, но при разном расположении его стержень сопротивляется изгибу по-разному. При изгибе важной геометрической характеристикой является статический момент площади сечения.
Статическим моментом сечения относительно данной оси называется сумма произведений элементарных площадей dA на
63
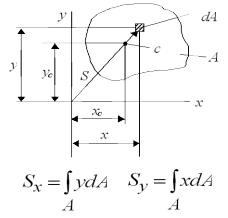
их расстояния до данной оси, которая распространяется на всю площадь (рис. 12.2).
Рис. 12.2
На основании теоремы Вариньона следует, что
Sx = ∫ydA = Ayc = ∑Ai yci ;
A
Sy = ∫xdA = Axc = ∑Ai xci .
A
Статический момент площади А относительно какойлибо оси равен произведению всей площади на расстояние от ее центра тяжести до этой оси. На основании последних выражений получим формулы для определения координат центра сечения:
ус = |
Sx |
= |
∑Ai yc |
; |
|||
A |
∑Ai |
||||||
|
|
|
|
||||
x = |
Sy |
|
= ∑Ai xci . |
||||
|
|||||||
c |
A |
|
∑Ai |
|
|||
|
|
|
|
||||
64
12.1. Моменты инерции сечения
Осевым моментом инерции сечения относительно данной оси называется сумма произведений элементарных площадей dA на квадрат их расстояний до данной оси, которая распространяется на всю площадь:
Jx = ∫y2dA,
A
J y = ∫x2dA.
A
Полярный момент инерции Jp равен сумме осевых моментов инерции Jx и Jy относительно любых двух взаимно перпендикулярных осей х и у, проходящих через полюс О:
J p = Jx + J y .
Центробежным моментом инерции сечения относительно осей координат называется сумма произведений элементарных площадей DA на их расстояния до этих осей, которая распространяется на всю площадь сечения А:
Jxy = ∫xy dA.
Примеры:
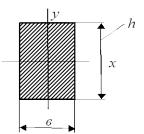
Прямоугольное сечение (рис. 12.3):
Рис. 12.3
65
Jx = вh3 ; 12
J y = h12в3 ;
Jxy = 0.
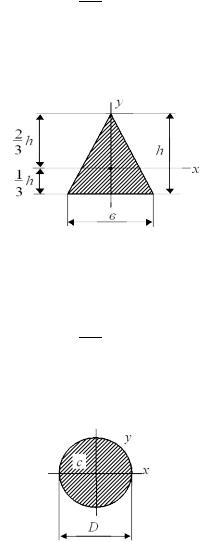
Треугольное сечение (рис. 12.4):
Рис. 12.4
Jx = вh3 ; 36
J y = h48в3 ;
Jxy = 0.
Круглое сечение (рис. 12.5):
Рис. 12.5 66