Условие прочности балки из пластичного материала имеет вид
σmax = Mz/Wz≤[σ].
Момент сопротивления для прямоугольного сечения, размеры которого b-h: WZ = bh2/6.
Момент сопротивления для балки круглого поперечного сечения Wz=πd 3/32.
14. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
14.1. Основные понятия
Выполнение условий прочности и жесткости по сравнению с допускаемыми нормами еще не обеспечивает способность конструкций выполнять предназначенные им функции.
Наряду с анализом прочности и жесткости необходим анализ устойчивости конструкций.
Исходное состояние равновесия тела назовем невозмущенным, отклонения его от состояния равновесия – возмущениями, а новое состояние равновесия – возмущенным.
Равновесие называется устойчивым, если при действии малых возмущений тело отклоняется от своего невозмущенного состояния равновесия незначительно. Если же состояние равновесия тела не обладает этим свойством, то оно называется неустойчивым.
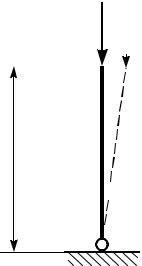
Рассмотрим абсолютно жесткий стержень, сжатый силой F и шарнирно закрепленный нижним концом. В вертикальном положении стержень удерживается пружиной, имеющей жесткость c (рис. 14.1). При повороте стержня на единичный угол в упругом шарнире возникает момент, равный c.
Стержень получил отклонение от вертикального положения (повернулся на угол ϕ), при этом если новое положение
стержня является равновесным, то уравнение Σm0=0 позволит получить следующее выражение:
Flsinϕ=cϕ. (14.1) 75
_ |
|
|
_ |
|
|||
|
|||
|
|||
F |
|
F |
|
|
|||
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
l
ϕ
0
Рис. 14.1
В этом случае рассматриваемая задача является нелинейной (нелинейность обусловлена конечным перемещением стержня).
Если угол ϕ достаточно мал, то можно положить sinϕ≈ϕ. В результате уравнение (14.1) заменяется линеаризованным:
(Fl – c)ϕ=0.
Первое из возможных решений, при ϕ = 0, означает, что при любом значении силы F соблюдается вертикальное положение равновесия стержня.
Второе решение (ϕ ≠ 0) возможно в том случае, когда обращается в нуль множитель Fl-c=0. Отсюда следует, что отклоненное положение равновесия имеет место только при
F=c/l=F*.
Таким образом, при F=F*, наряду с вертикальным положением равновесия стержня, возможно другое положение равновесия, как угодно близкое к первому. Силу F* называют критической силой.
76
При F<F* стержень имеет только одно вертикальное положение равновесия. При F=F* стержень начинает отклоняться от вертикального положения равновесия. При F>F* стержень отклонится от вертикального положения еще больше.
Таким образом, при F<F* вертикальное положение равновесия стержня является устойчивым, а при F>F* – неустойчивым. При F>F* происходит переход стержня от исходного вертикального (устойчивого) положения равновесия к отклоненному (неустойчивому) положению равновесия. Данный переход называют потерей устойчивости исходного положения равновесия стержня.
Потеря устойчивости может произойти при напряжениях, значительно меньше тех, которые допустимы с точки зрения прочности конструкции.
14.2. Формула Эйлера для критической силы
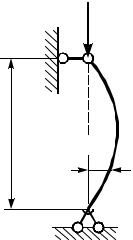
Рассмотрим сжатый стержень, шарнирно опертый по концам (рис. 14.2). Предположим, что стержень искривился, вследствие чего в нем появился изгибающий момент M=Fv.
_
F
l
z
V
0
Рис. 14.2
77
Равенство EIν |
= −M справедливо при малых прогибах и |
|
|
|
|
его можно представить в виде |
|
|
|
V + k2ν = 0 , |
(14.2) |
где k2=F/EI.
Однородное дифференциальное уравнение (14.2) имеет решение
V(z)=B cos kz + C sin kz.
Произвольные постоянные B и C определяются из граничных условий:
при z=0 v=0; при z=l v=0.
Из условия z=0 следует, что B=0. Таким образом, уравнение оси изогнутого стержня записывается так:
v=Csinkz.
Второе граничное условие позволяет получить
Csinkl=0.
Если предположить, что C≠0, то sinkl=0, и тогда получим kl=nπ, n=1,2,3,… .
В результате имеем F=n2π2EI/l2, при этом криволинейная форма равновесия стержня возможна только при фиксированных значениях сжимающей силы. При n=1 стержень изгибается с образованием одной полуволны синусоиды (рис. 14.3), при всех последующих n число полуволн соответственно равно n.
Наименьшее значение сила F принимает при n=1:
Fкр=π2EI/l2. (14.3)
Эта сила называетсякритической силой. Формула (14.3) была впервые получена в 1744 г. математиком Леонардом Эйлером.
Таким образом, Fкр представляет собой наименьшую сжимающую силу, при которой наряду с прямолинейной формой равновесия становится возможной другая (изгибная) форма равновесия.
78