9.3. Общие положения теории удара

Силы, действующие на тела, подразделяют на конечные силы, т.е. силы, изменяющие скорости точек в течение некоторого конечного промежутка времени, и силы мгновенные, или ударные, изменяющие скорости точек в течение весьма малого промежутка времени (0.1–0.01 с).

Силу, действующую в течение весьма малого промежутка времени, но достигающую при этом таких больших значений, что ее импульс за это время становится конечной величиной, называют мгновенной (ударной) силой.

Пусть F – ударная сила, τ – время действия этой силы, то-

τ

гда импульс за промежуток времени τ: S = ∫Fdt . Здесь S – ко-

0

нечная величина. Это возможно в случае, если величина силы

порядка 1/τ, где τ – малая величина. Импульс S называют ударным. Явление, при котором возникают мгновенные, или ударные, силы называютударом.

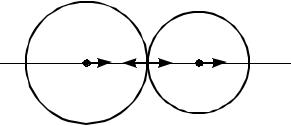
Рассмотрим на примере соударения двух тел А и В (рис. 9.3) процесс удара. Считаем, что контакт происходит в одной точке.

Рис. 9.3

Тело А в момент соприкосновения имеет скорость V1, а тело В – скорость V2 (допустим, что V1> V2). Общую нормаль к поверхности соударяющихся тел в точке их контакта назовем линией удара.

53

Если центры масс соударяющихся тел лежат на линии удара, то удар называют центральным. Центральный удар называют прямым, если скорости центров масс соударяющихся тел в начале удара направлены по линии удара. Тела считаются абсолютно гладкими. После момента соприкосновения оба тела деформируются, при этом скорость тела А уменьшается, а скорость тела В увеличивается. Процесс деформации заканчивается тогда, когда скорости тел станут равными [27]. Эту

часть явления удара называют фазой деформации τ1. Ударный

τ1

импульс силы F за фазу деформации S1 = ∫Fdt .

0

Импульс силы F (F = −F ) за эту же фазу обозначим

S1 : S1 = −S1 . Если тела упруги, то после деформации они вос-

станавливают свою форму целиком и полностью. Эту часть явления удара называют фазой восстановления (продолжи-

тельность этой фазы τ2). Импульс ударной силы, действующей на тело А, за эту фазу восстановления

τ

S2 = ∫Fdt ,

τ1

где τ=τ1+τ2 (время продолжительности удара).

Эффект действия ударной силы оценивается по ее импульсу – конечной величине. Теоремы, применяемые к удару, формулируют так, чтобы в них входили не ударные силы, а ударные импульсы.

По коэффициенту восстановления k=S2/S1 оценивают упругость соударяющихся тел.

При k=0 величина S2=0, т.е. фаза восстановления отсутствует – абсолютно неупругий удар.

В случае k=1 величина S2=S1, можно считать, что тела полностью восстанавливают свою форму (абсолютно упругий удар) – это фаза восстановления.

Удар называют упругим при 0<k<1, при этом происходит удар тел средней упругости.

54