6. ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

6.1. Динамические дифференциальные уравнения относительного движения материальной точки

Если к материальной точке приложены некоторые силы, то движение точки под их действием представляется различным образом при наблюдении с неподвижной системы отсчета и с системы отсчета, имеющей некоторое переносное движение относительно неподвижной системы. Все кинематические параметры точки, в частности и ускорения, различны в этих системах отсчета. Уравнение динамики материальной точки, отнесенное к «неподвижной» системе отсчета, имеет вид:

где m–масса точки; a–ускорение точки; Fk – силы, приложенные к точке.

Если воспользоваться кинематической теоремой Кориолиса о сложении ускорений для точки, можно представить вектор абсолютного ускорения точки в виде геометрической суммы векторов относительного, переносного ускорений и ускорения Кориолиса:

a=ar+ae+ak . (6.2)

Подставляя это выражение вместо a в (6.1), имеем:

Здесь введено F=∑Fk – равнодействующая всех непосредственно приложенных к рассматриваемой материальной точке сил.

Выражая из (6.3) m ar через остальные члены, получаем:

Из правой части равенства (6.4) можно видеть, что сила, действующая на точку и создающая ее относительное ускоре-

33

ние, состоит из трех слагаемых: непосредственно приложенной к точке силы F и двух дополнительных сил, наблюдаемых только в подвижной системе отсчета. Одну из этих сил называют переносной силой инерции и обозначают Фe:

Переносная сила инерции точки в ее относительном движении направлена противоположно вектору переносного ускорения точки и численно равна произведению массы точки на величину (модуль) переносного ускорения точки.

Другую силу называют силой инерции Кориолиса, векторное выражение которой имеет следующий вид:

Сила инерции Кориолиса направлена прямо противоположно ускорению Кориолиса точки и численно равна произведению массы точки на величину ускорения Кориолиса

[ak=2(ωe×Vr)].

Пользуясь равенствами (6.5) и (6.6), соотношение (6.4) можно представить в виде

Выражая относительное ускорение через вторую производную от вектора R, можно получить уравнение:

Уравнение (6.7′) выражает динамическую теорему Кориолиса: относительное движение точки происходит под действием не только непосредственно приложенной силы F, но и под действием переносной силы инерции Фe и силы инерции Кориолиса Фk.

34

6.2. Частные случаи динамической теоремы Кориолиса

Если переносное движение подвижной системы координат поступательное, то ωe=0, тогда ak=2(ωe×Vr)≡0 и Фk=-

mak≡0, а поэтому

Mar=F+Фe, т.е. относительное движение точки происходит под действием только двух сил: непосредственно приложенной и переносной силы инерции.

Если предположить дополнительно, что оси подвижной системы координат движутся равномерно, прямолинейно и параллельно осям неподвижной системы координат, то проекции силы F на оси каждой системы координат одинаковы.

Системы, по отношению к которым материальное тело может получать ускорение только вследствие реального воздействия на него других тел, но не вследствие движения системы координат, называются инерциальными системами координат.

Выясним, при каких условиях движение точки в подвижной системе координат является прямолинейным и равномерным с постоянной относительной скоростью Vr=const. Положим ar=0 в уравнении (6.7):

F+Фe+Фk=0 . (6.8)

Уравнение (6.8) выражает условие прямолинейного и равномерного движения точки в подвижной системе координат, имеющей переносное движение. Если в уравнении (6.8) положить Vr=0, что определяет условие собственно относительного равновесия точки (материальная точка, помещенная без начальной скорости в некоторое положение по отношению к подвижной системе координат, останется в этом положении равновесия), тогда ak=0 и сила инерции Кориолиса также равна нулю.

Условие (6.8) в этом случае имеет вид Фe+F=0, которое формулируется так: для относительного равновесия материальной точки в подвижной системе координат необходимо и достаточно, чтобы непосредственно приложенная к точке сила

и переносная сила инерции взаимно уравновешивались (Vr ωe, Vr=const).

35

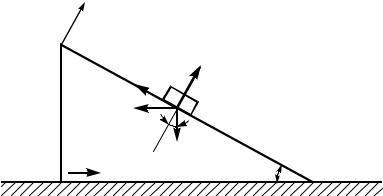
Пример. Груз А весом P скользит по боковой грани призмы В. Призма движется по горизонтальной плоскости с ускорением ae. Коэффициент трения скольжения f.

Определить ускорение груза по отношению к призме и давление груза на боковую грань призмы.

Решение. Движение груза А является сложным: относительное движение – движение по отношению к боковой грани; переносное – движение вместе с призмой.

К грузу приложены силы (рисунок): P – вес груза; N – нормальная реакция боковой грани; Fт.с. – сила трения сколь-

жения.

y

x

Для решения задачи воспользуемся методом динамики относительного движения: ко всем силам, приложенным к материальной точке, добавим силу инерции Фe в переносном движении и силу инерции Кориолиса. Так как переносное движение поступательное, то ak=0 и Фk=0. Сила инерции Фe в переносном движении Фe=Pae/g.

Составим дифференциальное уравнение относительного движения груза в проекции на ось X:

mXr = Psinα − Fm.c. −Фe cosα .

Учитывая, что Fт.с.=fN , получим

36