2.2.2. Уравнения первого порядка. Поле направлений

Рассмотрим обыкновенное дифференциальное уравнение 1-го порядка с правой частью f(x, y), определённой в области D ⊂ R²:

Здесь x независимая переменная (аргумент), y = y(x) неизвестная функция.

Если y = y(x) решение уравнения, то соответствующая интегральная кривая (график решения y = y(x)) в каждой своей точке (x, y(x)) имеет касательную с угловым коэффициентом

Через каждую точку (x, y) области D ⊂ R² можно провести небольшой отрезок с угловым коэффициентом k .

Выполнив такое построение для всех узлов некоторой прямоугольной сетки в области D ⊂ R² , получим изображение поля направлений.

Если узлы сетки расположены «достаточно часто» поле направлений дает полную картину поведения интегральных кривых.

На рисунках приведены изображение поля направлений и изображение поля направлений с несколькими интегральными кривыми.

Рассмотрев внимательно рисунки, можно увидеть, что отрезки, изображающие поле направлений действительно указывают направление касательных к интегральным кривым.

Можно видеть, что “аккуратно“ изображенное поле направлений дает достаточно полное представление о поведении интегральных кривых.

В инженерных задачах для того чтобы сформулировать содержательные утверждения об исследуемом процессе, бывает достаточно внимательно изучить поле направлений.

Дифференциальное уравнение задает поле направлений, которое позволяет судить о наиболее характерных особенностях поведения решений уравнения.

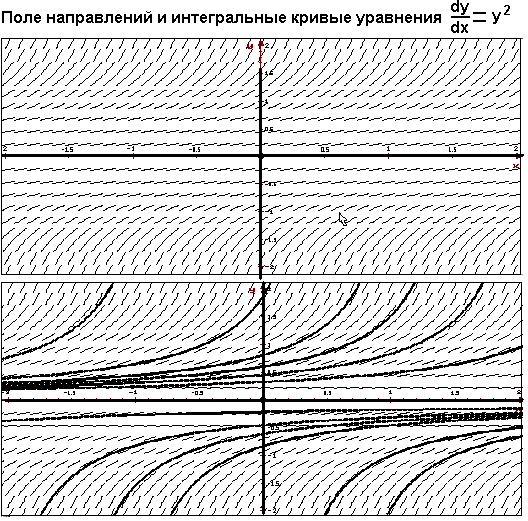
Пример №1

Рассмотрим обыкновенное дифференциальное уравнение 1-го порядка

с правой частью, определённой в области y ≠ 0.

На рисунках приведены изображения поля направлений уравнения и поля направлений с несколькими интегральными кривыми.

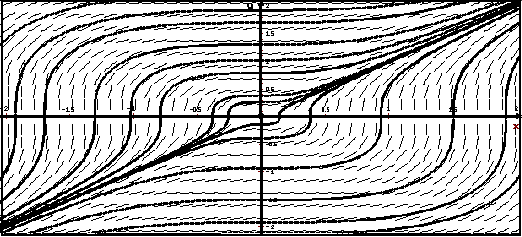
На рисунке видно, что в точках пересечения с осью абсцисс (y = 0) касательные к интегральным кривым перпендикулярны оси 0y . Это означает, в частности, что в этих точках скорость изменения решения возрастает до бесконечности.

Видно также, что по мере удаления точки (x, y(x)) (x → ∞,y(x) → ∞) скорость изменения решения стабилизируется − есть основания предполагать, что интегральные кривые имеют наклонную асимптоту.

Пример №2

Рассмотрим обыкновенное дифференциальное уравнение 1-го порядка с правой частью, определённой в области x ≠ 0, x² + (y + 0.5)² ≥ 0.5:

На рисунках приведено изображение поля направлений уравнения в области, где определена правая часть уравнения.

2.2.3. Автономные уравнения первого порядка

Автономным уравнением первого порядка называется уравнение вида

правая часть f(y) которого не зависит от x.

Решение y(x) ≡ 0 называется неподвижной точкой уравнения.

Для автономного уравнения решение задачи Коши

определяется равенством:

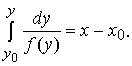
Например, дифференциальное уравнение

описывает движение материальной точки по оси x под действием внешних сил f(x). Координата точки x(t) в момент времени t – решение дифференциального уравнения. Скорость движения точки задана функцией f(x). В момент времени t координата x(t) точки, которая в начальный момент t₀ имела координату x₀, определяется равенством

При t → ∞ функция x(t) может быть ограниченной, может стремиться к конечному пределу, может ”уходить на бесконечность” (x(t) → ∞) или может быть неограниченной с каким-то более сложным поведением.

Пример №1

Исследуем поведение решений дифференциального уравнения y ' = cos πy .

В какой момент времени x₁ решение с начальным условием y(0) = 0 достигнет значения 0.5? Является ли точка y = 0.5 неподвижной точкой? Решения каких типов имеет уравнение?

Время x₁, за которое решение задачи Коши y ' = cosπy , y(0) = 0 достигнет значения 0.5, определяется равенством

Этот интеграл расходится. Значит точка, начавшая из нуля движение вдоль оси x, никогда не придет в точку y = 0.5 .

На рисунке видно, что интегральная кривая, проходящая через начало координат асимптотически приближается снизу к прямой y = 0.5 .

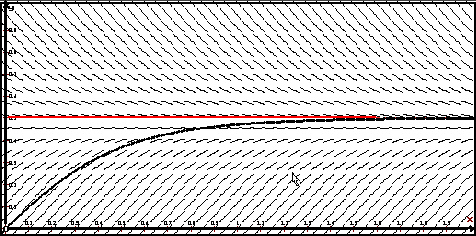
Точка y = 0.5 − неподвижная точка уравнения. Действительно, функция y = 0.5 является решением задачи Коши y ' = cos πy , y(0) = 0.5 . Это означает, что точка, начавшая движение из y = 0.5 остается на месте.

Для того чтобы ответить на вопрос о типах решений уравнения, изобразим его поле направлений.

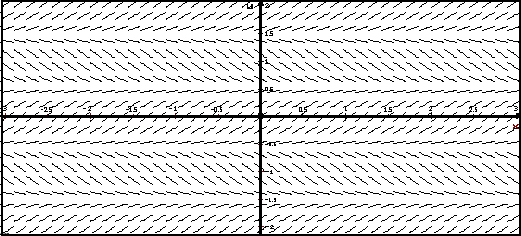
Видно, что уравнение имеет ограниченные решения в областях

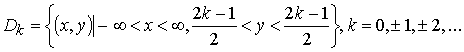
Уравнение имеет неподвижные точки: