4.4.2. Системы обыкновенных дифференциальных уравнений. Поведение решений

4.4.2.1. Устойчивость решений систем дифференциальных уравнений

Любая система дифференциальных уравнений описывает с определенной степенью точности реальный физический процесс.

Приборы, фиксирующие то или иное физическое явление, не совершенны. Может оказаться, что малая погрешность измерения начальных данных вызывает «ощутимые» изменения решений уравнений. В этой ситуации нельзя гарантировать, что выбранная математическая модель реально отражает описываемое ею физическое явление.

И, наоборот, если малые возмущения начальных условий мало изменяют решения на всем промежутке их существования, то соответствующую математическую модель следует признать удачной.

Так возникает важный для приложений вопрос: при каких условиях, математическая модель, описываемая системой дифференциальных уравнений, будет устойчивой.

Рассмотрим систему дифференциальных уравнений

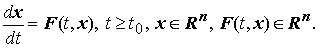
Полагаем, что выполнены условия теоремы существования и единственности решения задачи Коши.

Пусть некоторое фиксированное решение x = φ(t) этой системы существует при всех t ≥ t₀.

Решение x = φ(t) системы называется устойчивым по Ляпунову при t ≥ t₀ , если для любого ε > 0 существует число δ > 0 (зависящее, вообще говоря, от ε) такое, что:

− решение x = x(t) задачи Коши с начальным условием x(t₀) , | x(t₀) − φ(t₀) | < δ , существует при всех t ≥ t₀ ;

− для всех таких решений справедливо неравенство | x(t₀) − φ(t₀) | < δ , при всех t ≥ t₀ .

Геометрически это означает, что интегральные кривые x = x(t), близкие в момент t = t₀ к интегральной кривой x = φ(t), остаются близкими к ней и на всем промежутке [t₀,∞) .

Интегральные кривые и фазовые траектории, отвечающие устойчивым решениям, тоже называются устойчивыми.

На рисунке чёрным изображена устойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (1,0), и две, начинающиеся вблизи её траектории.

Решение x = φ(t) называется неустойчивым по Ляпунову при t ≥ t₀ , если оно не является устойчивым по Ляпунову, т.е. если существует такое число ε > 0, что для любого δ > 0 найдутся решения x = x_δ(t) и такое t₁= t₁(δ), что | x_δ(t₀) − φ(t₀) | < δ и | x_δ(t) − φ(t) | ≥ ε.

Геометрически это означает, что интегральные кривые x = x(t), близкие в момент t = t₀ к интегральной кривой x = φ(t) , "удаляются" от неё при t → ∞.

Интегральные кривые и фазовые траектории, отвечающие неустойчивым решениям, тоже называются неустойчивыми.

На рисунке чёрным изображена неустойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (0.2, 0), и две, начинающиеся вблизи её траектории.

Пример №1

Исследуем на устойчивость решение задачи Коши

Очевидно, что решение задачи − тривиальное решение, точка покоя системы, φ(t) ≡ 0,( т.е. φ₁(t) ≡ 0, φ₂(t) ≡ 0).

Докажем, что это тривиальное решение устойчиво при t > 0.

Решение системы, проходящее через точку (0, x₁(0) , x₂(0)), имеет вид:

Возьмём произвольное ε >0 и рассмотрим поведение при t > 0 тех решений x= x(t), которые удовлетворяют условию ‌ x(0) − φ(0) ‌< δ , где δ = ε >0:

Последнее неравенство справедливо при всех t > 0 .

Получили, что все, близкие в начальный момент к точке покоя решения, остаются вблизи неё всё последующее время. То есть точка покоя − устойчивое по Ляпунову решение системы.

На рисунке изображено несколько фазовых кривых системы (это эллипсы). Видно, что те из них, которые начинаются вблизи нуля, всегда вблизи нуля остаются.

Пример №2

Исследуем на устойчивость решение задачи Коши

Очевидно, что это решение задачи − тривиальное решение, точка покоя системы, φ(t) = 0,( т.е. φ₁(t) = 0, φ₂(t) = 0).

Докажем, что это нулевое решение не устойчиво при t > 0.

Легко видеть, что решение системы, проходящее через точку (0, x₁(0) , x₂(0)), имеет вид:

Рассмотрим поведение при t > 0 тех решений x= x(t), которые удовлетворяют условию ‌ x(0) − φ(0) ‌< δ, δ > 0 :

Выберем t достаточно большим, таким, чтобы

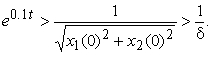
Отсюда следует, что как бы ни было мало δ > 0, существуют ε = 1,и t₁ = t₁(δ) = −ln(δ) и такое решение x(t), что при t ≥ t₁ справедливо неравенство | x(t) − 0 | > ε, т.е. тривиальное решение φ(t) ≡ 0 неустойчиво.

На рисунке видно, что фазовые кривые, которые начинаются вблизи нуля, через некоторое время покинут любую окрестность нуля.