2.1.7. Уравнения в полных дифференциалах

Уравнение

M(x, y)dx + N(x, y)dy = 0

называется уравнением в полных дифференциалах, если выражение в левой части уравнения является дифференциалом некоторой функции двух переменных F(x, y), т.е. если

dF(x, y) = M(x, y)dx + N(x, y)dy.

Тогда F(x, y) = C – общий интеграл уравнения. Здесь C – произвольная постоянная.

Уравнение M(x, y)dx + N(x, y)dy = 0 является уравнением в полных дифференциалах, тогда и только тогда, когда

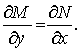
Пусть выражение M(x, y)dx + N(x, y)dy в левой части уравнения M(x, y)dx + N(x, y)dy = 0 является дифференциалом некоторой функции двух переменных F(x, y):

dF(x, y) = M(x, y)dx + N(x, y)dy.

Равенство dF(x, y) = M(x, y)dx + N(x, y)dy имеет место тогда и только тогда, когда функции M(x, y) и N(x, y) непрерывны вместе со своими частными производными первого порядка в некоторой односвязной област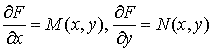и,

и

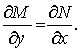
Отсюда следует, что уравнение M(x, y)dx + N(x, y)dy = 0 является уравнением в полных дифференциалах тогда и только тогда, когда

Пример №1

Уравнение 2xydx +(x² − y²)dy = 0 является уравнением в полных дифференциалах.

Действительно,

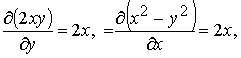
т.е. существует такая функция F(x, y), что

dF(x, y) = 2xydx +(x² − y²)dy.

Тогда

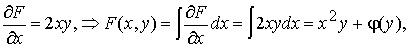
где φ(y) − неизвестная функция. Эту неизвестную функцию можно найти следующим образом:

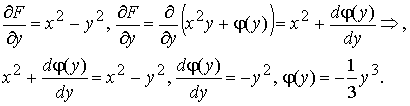
Тогда имеем

и можно записать общий интеграл уравнения:

2.2. Обыкновенные дифференциальные уравнения првого порядка. Поведение решений

2.2.1. Теорема существования и единственности решения задачи Коши

Рассмотрим обыкновенное дифференциальное уравнение 1-го порядка, записанное в нормальной форме:

Областью определения уравнения называется область D определения правой части уравнения f(x, y), D ⊂ R² .

Функция y = y(x) является решением задачи Коши

если y = y(x) дифференцируема на [a, b] , (x, y(x)) ∈ D для всех x из [a, b] , y(x₀) = y₀ , x₀∈[a, b], и при подстановке в уравнение обращает его в тождество:

Фундаментальным результатом теории обыкновенных дифференциальных уравнений является теорема существования и единственности решения задачи Коши:

Пусть функция f(x, y) и ее частная производная f_y(x, y) непрерывны в некоторой области D плоскости x0y и точка (x₀, y₀) принадлежит области D.

Тогда :

– в некоторой окрестности (x₀ − δ, x₀ + δ) точки x₀ существует решение задачи Коши

– если y = φ₁(x) и y = φ₂(x) два решения задачи Коши, то φ₁(x) = φ₂(x) на

(x₀ − δ, x₀ + δ) .

Геометрически это означает, что если условия теоремы выполнены, то через каждую точку (x₀, y₀) области D проходит единственная интегральная кривая уравнения.

Бесконечное множество решений уравнения

можно рассматривать как однопараметрическое семейство функций y = φ(x; x₀) – семейство решений задачи Коши

элементы которого различны для разных значений x₀ . Иными словами область D «расслаивается» на интегральные кривые y = φ(x; x₀) .

Важно понимать, что результат теоремы имеет локальный характер – существование и единственность решения гарантированы, вообще говоря, только в малой окрестности точки x₀ . Важно также понимать, что условия теоремы существования и единственности достаточные условия. Нарушение условий теоремы не означает, что решение задачи не существует либо что оно не единственно.

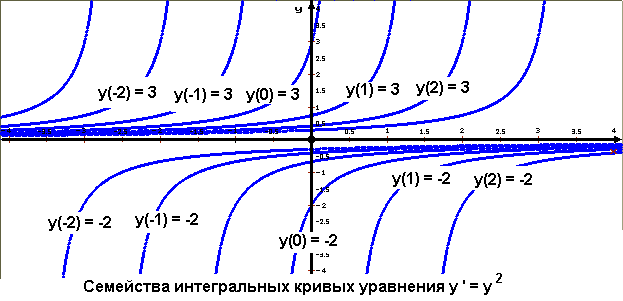
Пример №1

Рассмотрим задачу Коши

Условия теоремы существования и единственности задачи Коши выполнены на всей плоскости x0y: f(x, y) = y² и f_y(x, y) = 2y непрерывны всюду.

Общее решение уравнения имеет вид

Начальные условия y(x₀) = 3 и y(x₀) = − 2 определяют соответственно два решения

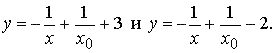
На рисунке изображено несколько интегральных кривых уравнения.

Пример №2

Рассмотрим задачу Коши

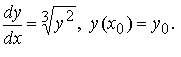
Здесь

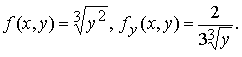
Правая часть уравнения f(x, y) непрерывна на всей плоскости x0y , а производная f_y(x, y) непрерывна при y ≠ 0 .

Начальное условие y(0) =0 определяет интегральную кривую y(x) = 0, а условие y(1) =1 − интегральную кривую y = x³ , т.е. через точку (0,0) проходят две интегральные кривые.

В то же время, через любую точку области D , не содержащую ось абсцисс (y ≠ 0) проходит единственная интегральная кривая.

На рисунке изображены интегральные кривые задачи Коши с начальными условиями y(0) =0 и y(1) =1: