3.5.2. Метод подбора построения частного решения неоднородного уравнения

Рассмотрим линейное неоднородное дифференциальное уравнение

y⁽ⁿ⁾ + a_n-1y^(n-1) + ... + a₁y' + a₀y = f(x).

Коэффициенты a_n-1, ... , a₁, a₀ − постоянные действительные числа, f(x) − непрерывная на [a;b] правая часть.

Общее решение этого уравнения имеет вид

y(x) = C₁y₁(x) + C₂y₂(x) + ... + C_ny_n(x) + y*(x),

где С₁,С₂, ...,С_n − произвольные постоянные, y₁(x), y₂(x), ..., y_n(x) − фундаментальная система решений однородного уравнения, y*(x) − частное решение неоднородного уравнения.

Частное решение y*(x) можно найти методом подбора, если правая часть уравнения − квазимногочлен − функция вида

f(x) = exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).

Здесь M_m(x) − многочлен степени m, N_n(x) − многочлен степени n, α и β − действительные числа.

Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в том, что частное решение уравнения отыскивают в виде

y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)) x^r,

где P_k(x) и Q_k(x) − многочлены степени k = max(n, m) с неизвестными коэффициентами,

P_k(x) = p_kx^k + p_k-1x^k-1 + ... + p₁x + p₀,

Q_k(x) = q_kx^k + q_k-1x^k-1 + ... + q₁x + q₀.

Для того чтобы найти неизвестные коэффициенты многочленов P_k(x) и Q_k(x), подставляем

y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx))

в уравнение и приравниваем в правой и левой части полученного равенства коэффициенты при

exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx), x²exp(αx)cos(βx), x²exp(αx)sin(βx), ..., x^kexp(αx)cos(βx), x^kexp(αx)sin(βx).

Полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.

Метод подбора применяется к ограниченному, но достаточно широкому классу правых частей, поскольку квазимногочленами являются функции вида:

M_k(x), M_k(x)exp(αx), M_k(x)cos(βx), M_k(x)sin(βx), exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).

Частное решение y*(x) можно найти методом подбора, если правая часть уравнения − квазимногочлен − функция вида

f(x) = exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx)).

Здесь M_m(x) − многочлен степени m, N_n(x) − многочлен степени n, α и β − действительные числа.

Метод подбора вычисления частного решения линейного неоднородного уравнения с квазимногочленом в правой части состоит в следующем.

Внимательно смотрим на правую часть уравнения и записываем число α ± βi.

Затем составим характеристическое уравнение однородного уравнения и найдем его корни. Возможны два случая: среди корней характеристического многочлена нет корня, равного числу α ± βi (нерезонансный случай) и среди корней характеристического многочлена есть r корней, равных числу α ± βi (резонансный случай).

Рассмотрим нерезонансный случай (среди корней характеристического многочлена нет корня, равного числу α ± βi) . Тогда частное решение уравнения будем искать в виде

y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)),

где P_k(x) и Q_k(x) − многочлены степени k = max(n,m) с неизвестными коэффициентами,

P_k(x) = p_kx^k + p_k-1x^k-1 + ... + p₁x + p₀,

Q_k(x) = q_kx^k + q_k-1x^k-1 + ... + q₁x + q₀.

Для того чтобы найти неизвестные коэффициенты многочленов P_k(x) и Q_k(x) , подставим y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx)) в уравнение и приравняем коэффициенты при exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx), x²exp(αx)cos(βx), x²exp(αx)sin(βx), ..., x^kexp(αx)cos(βx), x^kexp(αx)sin(βx).

Доказано, что полученная таким образом система 2k + 2 уравнений относительно 2k + 2 неизвестных имеет единственное решение.

Рассмотрим резонансный случай (среди корней характеристического многочлена есть r корней, равных числу α ± βi) . Тогда частное решение уравнения будем искать в виде

y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx))x^r,

где P_k(x) и Q_k(x) − многочлены степени k=max(n,m) с неизвестными коэффициентами.

Для того чтобы найти неизвестные коэффициенты многочленов P_k(x) и Q_k(x), подставляем y*(x) = exp(αx)(P_k(x)cos(βx) + Q_k(x)sin(βx))x^r в уравнение и приравниваем коэффициенты при exp(αx)cos(βx), exp(αx)sin(βx), xexp(αx)cos(βx), xexp(αx)sin(βx), x²exp(αx)cos(βx), x²exp(αx)sin(βx), ..., x^kexp(αx)cos(βx), x^kexp(αx)sin(βx).

Пример №1

Уравнением колебаний называют линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами

Однородное уравнение y'' + ω₀²y = 0 описывает свободные колебания материальной точки с частотой ω₀².

Неоднородное уравнение — колебания материальной точки под действием внешней периодической силы Fcosωx, частота которой ω.

Найдём общее решение уравнения колебаний в случае, когда частота свободных колебаний не совпадает с частотой внешней вынуждающей силы.

Характеристическое уравнение однородного уравнения λ² + ω₀² = 0 имеет пару комплексно сопряжённых корней λ_1,2 = ± i ω₀.

Фундаментальную систему решений однородного уравнения образуют функции cosω₀x, sinω₀x. Общее решение однородного уравнения имеет вид

y(x, C₁, C₂) = C₁cosω₀x + C₂sinω₀x.

Правая часть уравнения — квазимногочлен exp(αx)(M_m(x)cos(βx) + N_n(x)sin(βx))≡Fcosωx , у которого α = 0, β = ω, M_m(x)= M₀ = F, N_n(x)= 0, α ± iβ = iω.

Поскольку ω ≠ ω₀, среди корней характеристического уравнения нет корня, равного корню характеристического уравнения.

Будем искать частное решение неоднородного уравнения y*(x) в виде y*(x) = A cosω x + B sin ω x.

Подставим в уравнение:

y = A cosω x + B sin ω x, y' = −Aω sinω x + B ωcos ω x, y'' = −Aω² cosω x − Bω² sin ω x,

y'' + ω₀²y = −Aω² cosω x − Bω² sin ω x + ω₀²A cosω x + B sin ω x = A(−ω² + ω₀²)cosω x + B (−ω² + ω₀²)sinω x = Fcosωx.

Приравняв коэффициенты в левой и правой части уравнения A(−ω² + ω₀²)cosω x + B (−ω² + ω₀²)sinω x = Fcosωx,

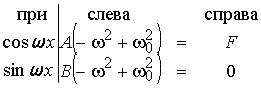
получим систему линейных уравнений,

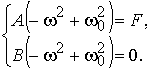
решение которой B = 0, A = F/(−ω² + ω₀²) и тогда частное решение неоднородного уравнения

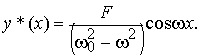
Теперь можно записать общее решение неоднородного уравнения