4.4.3.3. Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы второго порядка
Рассмотрим автономную систему второго порядка
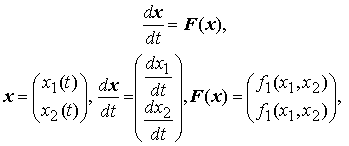
для которой справедлива теорема существования и единственности решения задачи Коши.
При описании интегральных кривых, фазовых траекторий и фазовой плоскости автономной системы 2-го порядка привычнее вместо переменных (x1,x2) использовать переменные (x,y) В дальнейшем будем записывать автономные системы 2-го порядка в виде:
Пусть x = φ(t) − решение автономной системы, определенное на отрезке [a;b]. Множество точек x = φ(t), t ∈ [a, b] − кривая в пространстве Rx,y2 − фазовая траектория системы, а пространство Rx,y2 − фазовая плоскость автономной системы.
Точка a называется положением равновесия (точкой покоя) автономной системы, если F(a) = 0 .
Равенство x = φ(t) , t ∈ [a,b] , или, что то же самое,
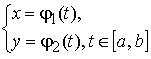
− параметрические уравнения фазовой траектории.
Интегральная кривая системы изображается в 3-х мерном пространстве Rx,y, t2 . Она задается уравнением
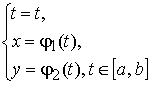
Соответствующая фазовая траектория − проекция интегральной кривой на фазовую плоскость.
Изобразив на фазовой плоскости несколько фазовых траекторий так, чтобы можно было убедительно предсказать поведение фазовой траектории, проходящей через любую точку фазовой плоскости (некоторой области фазовой плоскости) получим фазовый портрет автономной системы.
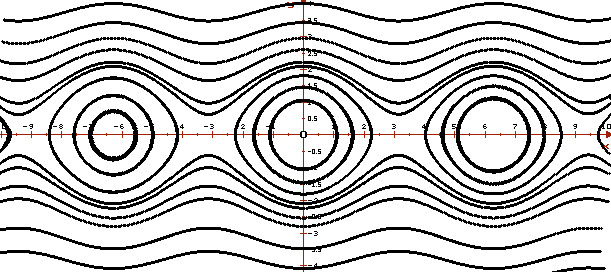
На рисунке приведено изображение фазовых портретов двух автономных систем. Видно, что траектории представленных систем ведут себя по-разному.
На верхнем рисунке приведен фазовый портрет системы, описывающей колебания математического маятника «без трения», на нижнем − колебания математического маятника «с трением».
4.4.3.4. Векторное поле автономной системы второго порядка
Если в каждой точке области G из Rn задан n-мерный вектор F(x), x ∈ G, то говорят, что в области G задано векторное поле.
Векторное поле непрерывно дифференцируемо, если непрерывно дифференцируема функция F(x).
Точки векторного поля, в которых F(x) = 0, называют особыми точками векторного поля.
Точка покоя автономной системы − особая точка векторного поля системы.
Автономная система x' = F(x) полностью определяется векторным полем F(x).
Рассмотрим автономную систему второго порядка
Пусть x = φ(t) − решение автономной системы, определенное на отрезке [a;b]. Фазовая траектория, соответствующая решению системы x = φ(t), определяется параметрическими уравнениями x = φ(t) , t ∈ [a;b], или, что тоже самое,
В каждой точке M0(x0, y0) этой гладкой фазовой кривой существует касательный вектор (x'(t0), y'(x0) = F(M0).
Иными словами, векторное поле F(x) автономной системы задаёт в каждой точке направление касательной к фазовой кривой, проходящей через эту точку.
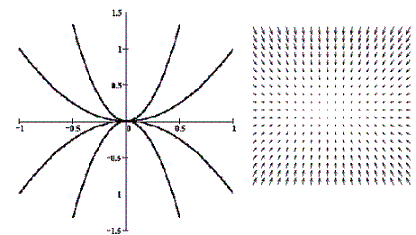
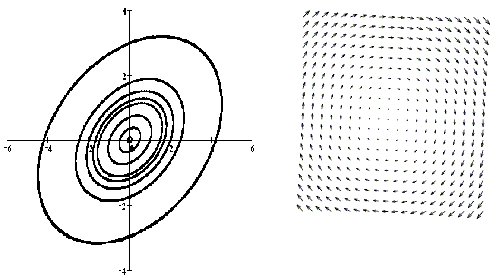
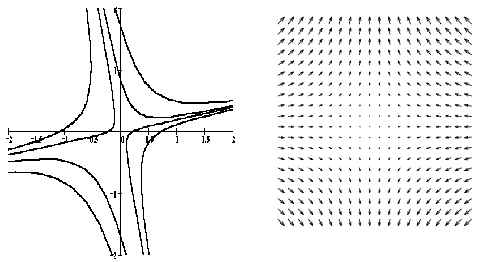
На рисунке приведены фрагменты векторных полей автономных систем и соответствующих фазовых портретов автономных систем с точками покоя разных типов.
Пример №1
Найдём в точках (0;1), (1;0) и (1;1) векторное поле автономной системы
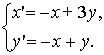
Вычислим векторное поле в заданных точках:
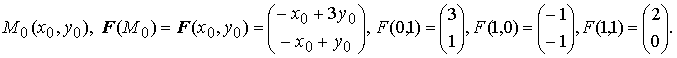
На рисунке изображён фрагмент векторного поля в окрестности точки покоя системы, содержащий, среди прочих, и вычисленные векторы.
