1.2. Системы оду. Основные понятия
Система обыкновенных дифференциальных уравнений n-го порядка
может быть записана в канонической форме:
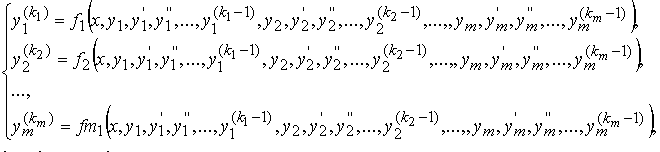
в нормальной форме
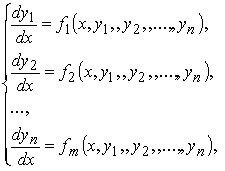
или в векторной форме
Здесь
При описании систем дифференциальных уравнений удобнее пользоваться векторной формой записи.
Решением системы обыкновенных дифференциальных уравнений Y' = F(x,Y) называется вектор-функция Y(x)=Φ(x), которая определена и непрерывно дифференцируема на промежутке (a;b) и удовлетворяет системе Y'=F(x,Y) на этом промежутке.
Задачей Коши для системы обыкновенных дифференциальных уравнений называется следующая задача: найти решение Y(x) системы Y' = F(x,Y) такое, что Y(x0) = Y0 . Здесь
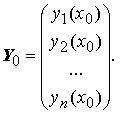
Частным решением системы дифференциальных уравнений называется решение какой-нибудь ее задачи Коши.
Вектор-функция Y = Y(x, C) = Y(x, C1,C2, … , Cn) , зависящая от n произвольных постоянных C1,C2, … , Cn называется общим решением системы дифференциальных уравнений на [a;b] , если:
– при любых допустимых значениях постоянных C1,C2, … , Cn функция Y(x, C) является решением системы на [a;b] ;
– какова бы ни была начальная точка (x0, Y0) из области определения правой части системы, существуют такие значения C*1,C*2, … , C*n постоянных C1, C2, … , Cn , что функция
Y(x, C*1,C*2, … , C*n) является решением задачи Коши Y(x0) = Y0 .
Пусть Y(x) = Φ(x) – решение системы, определенное на [a;b] . Тогда множество точек {Φ(x)}, x∈[a;b] – кривая в пространстве Rn .
Эту кривую называют фазовой траекторией или просто траекторией системы, а пространство Rn , в котором расположены фазовые траектории, фазовым пространством системы.
Пусть Y(x) = Φ(x) – решение системы Y' = F(x,Y) , определенное на [a,b] .
Интегральная кривая системы определяется уравнением Y = Φ(x) и изображается в (n + 1)-мерном пространстве Rn+1 .
Фазовая траектория – проекция интегральной кривой на пространство Rn.
Пример №1
Задача Коши для системы обыкновенных дифференциальных уравнений 2-го порядка в нормальной форме
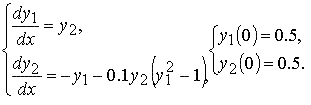
В векторной форме эта задача записывается следующим образом.
или
На рисунке изображены интегральная кривая (слева) и фазовая траектория (справа) задачи Коши для системы обыкновенных дифференциальных уравнений 2-го порядка
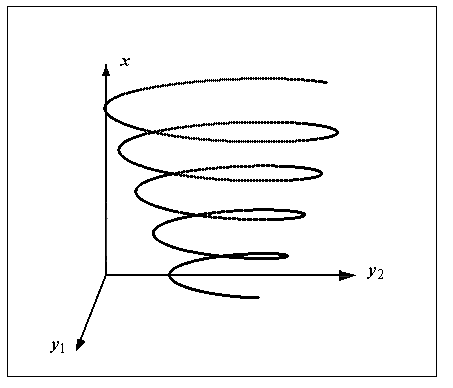
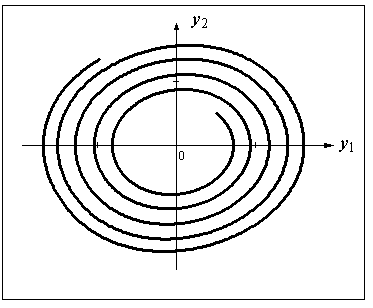
1.3. Связь оду высших порядков и систем оду
Задача Коши для любого дифференциального уравнения n-го порядка, записанного в нормальной форме,
y(n)= F(x, y, y', y'', … , y(n−1) ) = 0,
y(x0) = y0,
y'(x0) = y1,
y''(x0) = y2,
.................… ,
y(n−1) (x0) = yn−1 ,
может быть сведена к задаче Коши для системы дифференциальных уравнений n– го порядка.
Обозначим
z1(x) = y(x), z2(x) = y'(x), z3 (x) = y''(x), … , zn( x) = y (n − 1)(x ).
Тогда
F(x, y, y', y'', … , y(n−1)) ≡ F(x, z1, z2, z3, … , zn)
и задача Коши для уравнения записывается в виде задачи Коши для системы
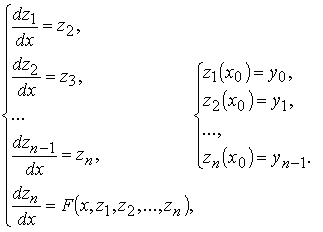
Эта задача в векторной форме записывается в виде:
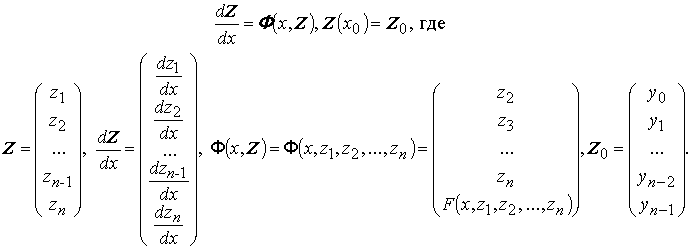
Пример №1
Движение материальной точки массы m под действием силы F описывается вторым законом Ньютона ma = F.
Пусть точка движется по оси 0x и x(t) – ее абсцисса в момент времени t. Тогда функция x(t) является решением дифференциального уравнения 2-го порядка
Чтобы определить положения материальной точки, движущейся по некоторому закону во все моменты времени t, достаточно знать ее положение x0 и скорость v0 в некоторый начальный момент времени t0 . Иными словами, чтобы выделить единственное решение уравнения движения материальной точки, достаточно задать два начальных условия x(t0) = x0 , x'(t0) = v0.
В нормальной форме соответствующая задача Коши записывается в виде:
Сформулируем эквивалентную задачу Коши для системы дифференциальных уравнений второго порядка.
Будем использовать принятые в механике обозначения: x(t) – абсцисса точки в момент времени t, v(t) – скорость точки в момент времени t, x0 и v0 – абсцисса и скорость точки в момент времени t0. Тогда:
Имеем задачу Коши для системы дифференциальных уравнений второго порядка.
2. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
2.1. Обыкновенные дифференциальные уравнения первого порядка.
Методы решения
2.1.1. Дифференциальные уравнения первого порядка. Основные понятия
Уравнение
F(x, y, y ') = 0,
где y = y(x) – неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.
Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b) .
График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.
Дифференциальное уравнение 1-го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.
Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x0) = y0, называется задачей Коши (или начальной задачей).
Условие y(x0) = y0 – начальное условие.
Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1-го порядка, называется частным решением уравнения.
Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.
Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения.
Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:
Уравнения первого порядка часто записывают в дифференциальной форме:
M(x, y)dx + N(x, y)dy = 0.
Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y).
Пример №1
Решением уравнения
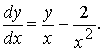
при всех x ≠ 0 является функция
Действительно, подставив выражение для y(x) в левую
и в правую часть уравнения
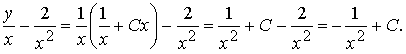
получили тождественное равенство
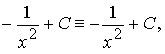
справедливое при всех x ≠ 0 и при произвольных значениях константы C.
Пример №2
Решением задачи Коши
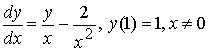
является функция
Действительно, подставив выражение для y(x) в левую и в правую часть уравнения, получим тождественное равенство:
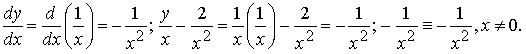
Начальное условие тоже, очевидно, выполнено:
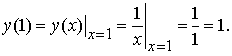
Пример №3
Равенство
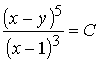
определяет при всех x ≠ 1 общий интеграл уравнения
Действительно.
Продифференцировав равенство для общего интеграла по x и вычислив производную искомого решения y(x) по x, получим тождественное равенство, справедливое при всех x ≠ 1 и при произвольных значениях константы C:
Пример №4
Равенство
определяет при всех x ≠ 1 частный интеграл задачи Коши
Продифференцировав равенство для частного интеграла по x и вычислив производную искомого решения y(x) по x, получим тождественное равенство, справедливое при всех x ≠ 1:
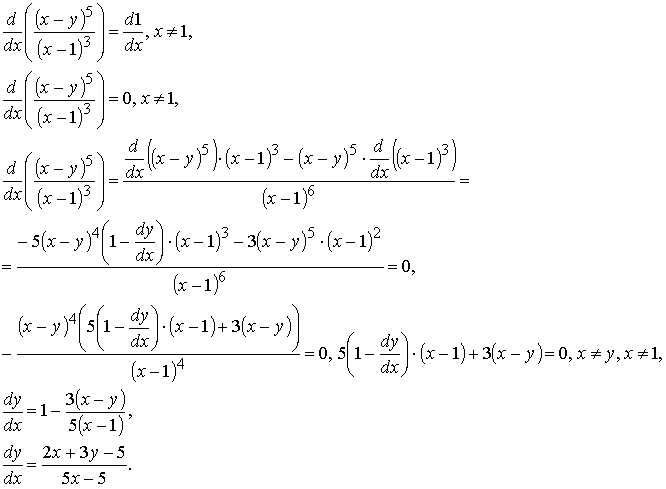
Условия Коши тоже, очевидно, выполнены:
