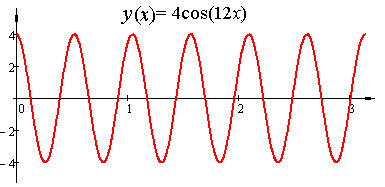- •Оглавление
- •Введение
- •1. Обыкновенные дифференциальные уравнения и системы
- •1.1. Обыкновенные дифференциальные уравнения. Основные понятия
- •1.2. Системы оду. Основные понятия
- •1.3. Связь оду высших порядков и систем оду
- •2.1.2. Уравнения с разделяющимися переменными
- •2.1.3. Однородные уравнения 1-го порядка
- •2.1.4. Уравнения, приводящиеся к однородным
- •2.1.5. Линейные уравнения первого порядка
- •2.1.6. Уравнения Бернулли
- •2.1.7. Уравнения в полных дифференциалах
- •2.2. Обыкновенные дифференциальные уравнения првого порядка. Поведение решений
- •2.2.1. Теорема существования и единственности решения задачи Коши
- •2.2.2. Уравнения первого порядка. Поле направлений
- •2.2.3. Автономные уравнения первого порядка
- •2.2.4. Устойчивость решений обыкновенных дифференциальных уравнений первого порядка
- •2.2.5. Асимптотическая устойчивость решений обыкновенных дифференциальных уравнений первого порядка
- •2.3. Метод изоклин
- •3. Обыкновенные дифференциальные уравнения высших порядков
- •3.1. Обыкновенные дифференциальные уравнения высших порядков. Понижение порядка
- •3.1.1. Понижение порядка обыкновенного дифференциального уравнения. Введение
- •3.1.2. Уравнения, не содержащие независимой переменной
- •3.1.3. Уравнения, не содержащие искомой функции
- •3.1.4. Уравнения с однородной правой частью
- •3.2. Линейные однородные дифференциальные уравнения n-го порядка
- •3.2.1. Линейные однородные дифференциальные уравнения n-го порядка. Введение
- •3.2.2. Свойства решений линейного уравнения. Принцип суперпозиции
- •3.2.3. Существование и единственность решения задачи Коши
- •3.2.4. Линейные уравнения второго порядка. Гармонические колебания
- •3.2.5. Линейные уравнения втрого порядка. Ангармонические колебания
- •3.2.6. Линейные уравнения второго порядка. Уравнение Ньютона
- •3.3. Линейная зависимость и линейная независимость системы функций
- •3.3.1. Линейная зависимость и линейная независимость системы функций
- •3.3.2. Определитель Вронского
- •3.3.3. Исследование линейной независимости системы функций
- •3.3.4. Линейная независимость решений линейного дифференциального уравнения
- •3.4. Структура решения линейного однородного дифференциального уравнения n-го порядка
- •3.4.1. Фундаментальная система решений однородного линейного дифференциального уравнения
- •3.4.2. Структура общего решения линейного однородного уравнения
- •3.4.3. Структура общего решения линейного неоднородного уравнения
- •3.4.4. Метод вариации произвольных постоянных отыскания частного решения
- •3.5. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •3.5.1. Решение однородного уравнения с постоянными коэффициентами
- •3.5.2. Метод подбора построения частного решения неоднородного уравнения
- •3.5.3. Уравнение Эйлера
- •4. Системы дифференциальных уравнений
- •4.1. Системы обыкновенных дифференциальных уравнений. Основные понятия
- •4.2. Фазовое пространство. Фазовые траектории
- •4.3. Существование и единственность решения задачи Коши
- •4.4. Интегрирование систем дифференциальных уравнений методом исключения
- •4.4.1. Линейные системы обыкновенных дифференциальных уравнений. Структура
- •4.4.1.1. Линейные системы обыкновенных дифференциальных уравнений. Основные понятия
- •4.4.1.2. Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений
- •4.4.1.3. Структура общего решения однородной линейной системы дифференциальных уравнений
- •4.4.1.4. Структура общего решения неоднородной линейной системы дифференциальных уравнений
- •4.4.1.5. Построение фундаментальной матрицы решений однородной линейной системы дифференциальных уравнений с постоянными коэффициентами методом Эйлера
- •4.4.2. Системы обыкновенных дифференциальных уравнений. Поведение решений
- •4.4.2.1. Устойчивость решений систем дифференциальных уравнений
- •4.4.2.2. Устойчивость и асимптотическая устойчивость по Ляпунову
- •4.4.2.3. Устойчивость положения равновесия линейных систем оду
- •4.4.2.4. Устойчивость точек покоя нелинейных систем по линейному приближению
- •4.4.2.5. Неустойчивость по линейному приближению точек покоя нелинейных систем
- •4.4.3. Автономные системы дифференциальных уравнений
- •4.4.3.1. Автономные системы. Основные понятия
- •4.4.3.2. Свойства фазовых траекторий
- •4.4.3.3. Фазовая плоскость, фазовые кривые, фазовый портрет автономной системы второго порядка
- •4.4.3.4. Векторное поле автономной системы второго порядка
- •4.4.3.5. Точки покоя линейной автономной системы второго порядка с постоянными коэффициентами
- •4.4.4. Численное интегрирование дифференциальных уравнений первого порядка
- •4.4.4.1. Задача Коши. Общие замечания. Постановка задачи
- •4.4.4.2. Метод Эйлера
- •4.4.4.3. Модифицированный метод Эйлера
- •4.4.4.4. Метод Рунге-Кутта
- •2. Решение уравнения модифицированным методом Эйлера:
- •3. Решение уравнения методом Рунге-Кутта:
- •4. Аналитическое решение заданного уравнения:
- •5. Сравнение точного решения и приближенных решений исходного дифференциального уравнения:
- •Библиографический список
- •Обыкновенные дифференциальные уравнения
3.2.2. Свойства решений линейного уравнения. Принцип суперпозиции
Рассмотрим линейное дифференциальное уравнение n-го порядка
y(n) + an-1(x)y(n-1) + ... + a1(x)y' + a0(x)y = f(x).
с непрерывными коэффициентами an-1(x), an-2(x), ..., a1(x), a0(x) и непрерывной правой частью f(x).
Принцип суперпозиции основан на следующих свойствах решений линейных дифференциальных уравнений.
1. Если y1(x) и y2(x) – два решения линейного однородного дифференциального уравнения
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0
то любая их линейная комбинация y(x) = C1y1(x) + C2y2(x) является решением этого однородного уравнения.
2. Если y1(x) и y2(x) – два решения линейного неоднородного уравнения L(y) = f(x) , то их разность y(x) = y1(x) − y2 (x) является решением однородного уравнения L(y) = 0 .
3. Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма любого фиксированного (частного) решения неоднородного уравнения и некоторого решения однородного уравнения.
4. Если y1(x) и y2(x) – решения линейных неоднородных уравнений L(y) = f1(x) и L(y) = f2(x) соответственно, то их сумма y(x) = y1(x) + y2(x) является решением неоднородного уравнения L(y) = f1(x) + f2(x).
Обычно именно это последнее утверждение называют принципом суперпозиции.
3.2.3. Существование и единственность решения задачи Коши
Линейным дифференциальным уравнением n-го порядка называется уравнение
y(n) + an-1(x)y(n-1) + ... + a1(x)y' + a0(x)y = f(x),
в которое неизвестная функция y = y(x) и все ее производные входят линейно.
Справедлива следующая теорема существования и единственности решения задачи Коши для линейного уравнения.
Если в уравнении y(n) + an-1(x)y(n−1) + ... + a1(x)y' + a0(x)y = f(x) все коэффициенты ai(x) и правая часть f(x) непрерывны на отрезке [a;b], то задача Коши для этого уравнения с начальными условиями
y(a) = y0, y '(a) = y10 , ..., y(n −1) (a) = yn0
имеет единственное на всем отрезке [a;b] решение y = y(x).
Следует понимать, что теорема имеет «глобальный» характер – решение существует и единственно всюду, где непрерывны коэффициенты и правая часть уравнения.
3.2.4. Линейные уравнения второго порядка. Гармонические колебания
Рассмотрим линейное однородное дифференциальное уравнение 2-го порядка (ω>0 – постоянная величина)
y '' + ω2 y = 0 .
Легко видеть, что общее решение этого уравнения имеет вид
y(t) = C1cos(ωt) + C2sin(ωt) .
Его можно записать в виде
y(t) = Acos(ωt − φ) ,
![]()
Для произвольной точки (t0, y0, y1) решение задачи Коши y(t0) = y0, y'(t0) = y1 существует и единственно на всей числовой оси.
Пусть t0 = 0. Решение задачи Коши y(0) = y0, y'(0) = y1 имеет вид
y(x) = Acos(ωt − φ) ,
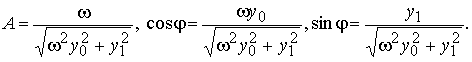
Будем считать, что y(t) – координата частицы в момент времени t . Частица движется по оси y из начальной точки y0 с положительной скоростью y1 > 0 .
Поскольку |y(x)| = |Acos(ωt − φ)| ≤ A , то частица будет двигаться по оси внутри отрезка [− A,A] .
Сначала частица движется вправо до точки y = A . В точку y = A она придет в момент времени t = (π + φ)/ω, (когда y(t) = Acos(ωt − φ) = A).
Затем частица движется влево до точки y = − A . В точку y = − A частица придет в момент времени t = (2π + φ)/ω, (когда y(t) = Acos(ωt − φ) = − A).
Понятно, что частица совершает периодические колебания на отрезке [− A, A] с периодом T = 2π/ω .
Число A называется амплитудой колебаний. Число ω называется частотой колебаний. Период колебаний T = 2π/ω не зависит от амплитуды.
На рисунке изображены пути трех частиц, движение которых описывается уравнением y '' + 4y = 0 .
Частицы движутся со скоростью y1 = 1 из начальных точек y0 = − 2, − 1, 0:

Физическая система, которая описывается уравнением y '' + ω2 y = 0 , называется гармоническим осциллятором.
Это малые колебания маятника, малые колебания под действием силы тяжести груза, подвешенного на упругой пружине, электрические колебания в контуре, состоящем из емкости и индуктивности и т.п. |
Пример №1
Запишем дифференциальное уравнение малых колебаний маятника c периодом колебаний T = π/6 и амплитудой 4.
Поскольку дифференциальное уравнение, описывающее малые колебания маятника с периодом T = 2π/ω имеет вид y '' + ω2 y = 0, то колебания маятника с периодом T = π / 6 описываются уравнением с параметром ω = 2π/T = 12:
y '' + 144 y = 0.
Амплитуду колебаний определим из начальных условий y(0) = 4 , y'(0) = 0 .
Действительно, поскольку, y(t) = C1cos(ωt) + C2sin(ωt), то y(0) = C1cos(0) + C2sin(0) = С1 = 4, y '(0) = − ωC1sin(0) + ωC2cos(0) = ωC2 = 0, С1 = 4, С2 = 0, y(t) = 4cos(12t) ,
т.е. амплитуда колебаний равна 4 .
Итак, малые колебания маятника c периодом колебаний T = π/6 и амплитудой 4 описываются решением y(t) = 4cos(12t) задачи Коши
y '' + 144 y = 0, y(0) = 4 , y '(0) = 0.