Введение

Обыкновенные дифференциальные уравнения применяются для описания многих процессов реальной действительности. Трудно представить себе область науки или производства, в которой не возникала необходимость использования дифференциальных уравнений. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторая физическая величина (перемещение тела, пластовое давление жидкости в фиксированной точке, концентрация вещества, объем продаж продукта) оказывается меняющейся современем под воздействием тех или иных факторов, то, как правило, закон ее изменения по времени описывается именно дифференциальным уравнением, т.е. уравнением, связывающим исходную переменную как функцию времени и производные этой функции. Независимой переменной в дифференциальных уравнениях может выступать не только время, но и другие физические величины: координата, цена продукта и т.д. Решение уравнения с анализом его зависимости от параметров задачи и начального состояния системы позволяет установить общие закономерности изменения исходной физической величины. В этой связи изучение обыкновенных дифференциальных уравнений в рамках курса высшей математики имеет принципиальное теоретическое и прикладное значения для подготовки современного специалиста.

1. Обыкновенные дифференциальные уравнения и системы

1.1. Обыкновенные дифференциальные уравнения. Основные понятия

Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида

,

где F – известная функция (n + 2)-х переменных, x – независимая переменная из интервала (a,b), y(x) – неизвестная функция. Число n называется порядком уравнения.

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a,b), если она n раз дифференцируема на (a,b) и при подстановке в уравнение обращает его в тождество.

Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме:

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия.

Чтобы выделить единственное решение уравнения n-го порядка обычно задают n начальных условий

y(x₀) = y₀, y'(x₀) = y₁,  y''(x₀) = y₂,  … , y^{(n − 1)}(x₀) = y_{n − 1}.

 Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения

F(x, y(x), y'(x), y''(x),…, y^{(n )}(x)) = 0,  x > x₀,

удовлетворяющего условиям

y(x₀) = y₀, y'(x₀) = y₁,  y ''(x₀) = y₂,…, y^{(n − 1)}(x₀) = y_{n − 1}.

Условия y(x₀) = y₀, y'(x₀) = y₁,  y''(x₀) = y₂, …, y^{(n − 1)}(x₀) = y_{n −1} называются начальными данными, начальными условиями или данными Коши.

Любое конкретное решение y = φ(x) уравнения n –го порядка

F(x, y(x), y'(x), y''(x),…, y^{(n )}(x)) = 0,

называется частным решением.

  Общим решением дифференциального уравнения

F(x, y(x), y'(x), y''(x),…, y^{(n )}(x)) = 0

называется функция

y = Ф(x, С₁,С₂,…,С_n),

содержащая некоторые постоянные (параметры) С₁, С₂,…, С_n, и обладающая следующими свойствами:

1. Ф(x, С₁, С₂,…, С_n) является решением уравнения при любых допустимых значениях С₁,С₂,…, С_m;

2. для любых начальных данных y(x₀) = y₀, y'(x₀) = y₁,  y''(x₀) = y₂,…, y^{(n − 1)}(x₀) = =y_{n − 1}, для которых задача Коши имеет единственное решение, существуют значения постоянных С₁= A₁, С₂= A₂,…, С_n= A_n, такие, что решение y = Ф(x, A₁, A₂,…, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f (x, y) = 0 или G(x, y,С₁, С₂,...,С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

 Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Для решения уравнений, которые не интегрируются в квадратурах, применяются приближенные или численные методы.

Задача теории обыкновенных дифференциальных уравнений – исследование общих свойств решений, развитие точных, асимптотических и численных методов интегрирования уравнений.

Пример №1

Пусть f(x) – непрерывная на (a;b) функция и y(x) – ее первообразная. Тогда

y '(x) = f(x)

т.е. для отыскания первообразной получено дифференциальное уравнение 1-го порядка.

Решения этого уравнения известны:

где С – произвольная постоянная, x ∈ (a;b), x₀ – некоторая точка из (a;b).

Чтобы выделить какое-то решение в задаче о вычислении первообразной, достаточно задать значение y(x) в какой-нибудь точке (a;b), например, y(x₀) = y₀.

Тогда решением задачи y '(x) = f(x), y(x₀) = y₀ является функция

Пример №2

Движение материальной точки массы m под действием силы F описывается вторым законом Ньютона ma = F.

Пусть точка движется по оси 0x и x(t) – ее абсцисса в момент времени t. Тогда функция x(t) является решением дифференциального уравнения 2-го порядка

Чтобы записать одномерное уравнение движения материальной точки в нормальной форме, достаточно разделить обе его части на m:

Чтобы определить положения материальной точки, движущейся по некоторому закону во все моменты времени t, достаточно знать ее положение x₀ и скорость v₀ в некоторый начальный момент времени t₀.

Иными словами, чтобы выделить единственное решение уравнения движения материальной точки, достаточно задать два начальных условия x(t₀) = x₀ , x'(t₀) = v₀.

Пример №3

На рисунке приведен график решения дифференциального уравнения 2-го порядка, описывающего изменение объема производства в некоторой замкнутой экономической системе:

y'' + 2ky' + ω²y = 0, k = 0.1, ω² = 0.25,

Колебания решений около нуля соответствуют периодам спада и подъема в экономике.

На следующих рисунках приведены графики решений дифференциального уравнения 2-го порядка y '' + 0.2y ' + 0.25y = 0 (k = 0.2, ω² = 0.25), для различных начальных условий, которые обозначены на рисунках:

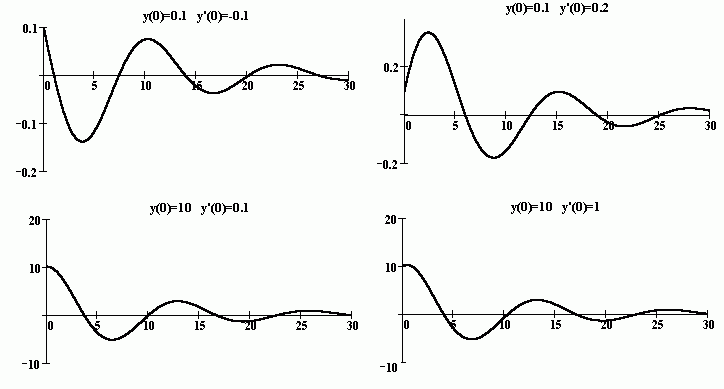
Уравнения такого вида, вообще говоря, при различных значениях k ≥ 0 и ω описывают затухающие колебания.

Пример №4

Для уравнения (y '')² = (1 + (y ')²)³

равенство ( x − C₁)² + (y − C₂)² − 1 = 0 определяет общий интеграл, а x² + y² − 1 = 0 определяет частный интеграл, соответствующий, начальным данным y(0) = 1, y '(0) = 0.

Пример №5

Уравнение движения материальной точки

не интегрируется в квадратурах при произвольной правой части. Оно интегрируется в квадратурах если сила F зависит только от одной переменной:

Для решения уравнений, которые не интегрируются в квадратурах, применяются приближенные и численные методы.