4.3. Существование и единственность решения задачи Коши

Рассмотрим систему обыкновенных дифференциальных уравнений n–го порядка

или

Задачей Коши для этой системы называется следующая задача: найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x₀)=Y₀, где Y₀ − некоторый постоянный вектор.

Справедлива следующая теорема о существовании и единственности решения задачи Коши.

Теорема: Пусть в области D из Rⁿ⁺¹ непрерывны все компоненты вектора правой части F(x,Y) и их частные производные по Y:

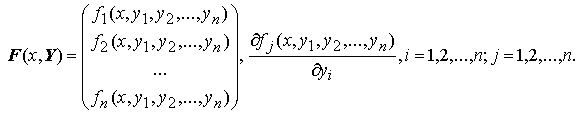
Тогда, какова бы ни была начальная точка (x₀,Y₀) ≡ (x₀,y₁₀ ,y₂₀, … ,y_n0) ∈ D, существует такой отрезок [x₀ − h; x₀ + h] , что задача Коши Y' = F(x,Y), что Y(x₀)=Y₀ имеет единственное решение.

Важно понимать, что эта теорема имеет локальный характер: существование решения Y = Y(x) гарантируется лишь в достаточно малой окрестности точки x₀ , ( h > 0 может оказаться достаточно малым).

Важно также понимать, что теорема содержит только достаточные условия существования и единственности решения − при нарушении условий теоремы задача Коши может иметь или не иметь решений, может иметь несколько решений.

Пример №1

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка:

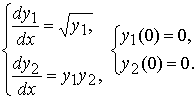
Легко проверить, что задача имеет два решения:

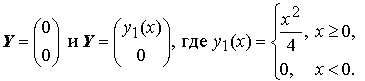
Нарушение единственности объясняется тем, что нарушены условия теоремы существования и единственности решения задачи Коши. Действительно

частная производная функции f₁(x,y₁,y₁) по y₁ разрывна в начальной точке (0,0,0).

4.4. Интегрирование систем дифференциальных уравнений методом исключения

Системы дифференциальных уравнений n-го порядка можно решать сведением к уравнению n-го порядка. Такой метод решения систем называется методом исключения.

Рассмотрим, например, нормальную систему дифференциальных уравнений 2-го порядка

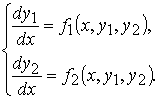
Исключим функцию y₂. Для этого сначала выразим y₂ через x и y₁ из первого уравнения системы, затем продифференцируем по x первое уравнение системы, заменяя y₂ полученным для него выражением, а производную y₂ − правой частью второго уравнения системы:

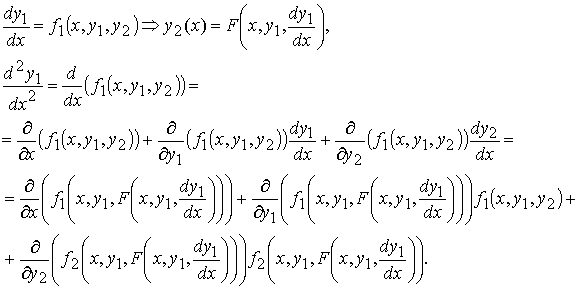
Получили обыкновенное дифференциальное уравнение 2-го порядка

Таким же образом решают методом исключения произвольные системы n-го порядка: дифференцируют уравнения системы и, последовательно исключая функции y₂, ..., y_n и их производные, сводят систему к одному дифференциальному уравнению n-го порядка относительно y₁.

Пример №1

Рассмотрим, например, нормальную систему дифференциальных уравнений 2-го порядка

Исключим искомую функцию y₂. Для этого сначала найдём y₂ из первого уравнения системы, а затем продифференцируем первое уравнение системы, исключив из него y₂ (для выражения производной используем второе уравнение системы):

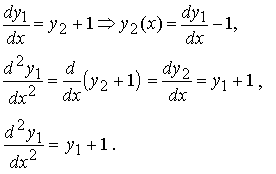
Получили обыкновенное дифференциальное уравнение 2-го порядка

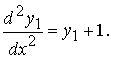
Это линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами y₁'' − y₁ = 1 нетрудно решить методом Эйлера (методом подбора). Его решение:

Теперь легко найти y₂:

Так методом исключения получено решение системы обыкновенных дифференциальных уравнений 2-го порядка

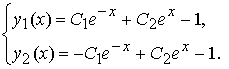
Проверить правильность решения можно устно.