4.4.3.5. Точки покоя линейной автономной системы второго порядка с постоянными коэффициентами

Рассмотрим линейную автономную систему 2-го порядка с постоянными коэффициентами x' = A·x :

Такая система имеет единственную точку покоя x ≡ 0, x=0, y=0, (0,0).

Характер точки покоя (её устойчивость, асимптотическую устойчивость, неустойчивость) можно установить по собственным значениям λ₁, λ₂ матрицы системы A.

Если λ₁, λ₂ − разные действительные отрицательные числа, то точка покоя асимптотически устойчива, такая точка покоя называется устойчивый узел.

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого узла.

Если λ₁, λ₂ − разные действительные положительные числа, то точка покоя неустойчива, такая точка покоя называется неустойчивый узел.

На рисунке приведен фрагмент фазового портрета в окрестности неустойчивого узла.

Если λ₁, λ₂ − действительные числа разных знаков, то точка покоя неустойчива, такая точка покоя называется седло.

На рисунке приведен фрагмент фазового портрета в окрестности седла.

Если λ₁, λ₂ − комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ ≤ 0, то точка покоя устойчива.

Если λ₁, λ₂ − комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ = 0, то точка покоя устойчива, но не асимптотически устойчива, такая точка покоя называется центром.

На рисунке приведен фрагмент фазового портрета в окрестности центра.

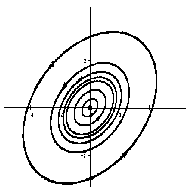
Если λ₁, λ₂ − комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ < 0, то точка покоя асимптотически устойчива, такая точка покоя называется устойчивым фокусом.

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого фокуса.

Если λ₁, λ₂ − комплексные числа, λ_1,2= Reλ ± iImλ, и Reλ > 0, то точка покоя неустойчива, такая точка покоя называется неустойчивым фокусом.

На рисунке приведен фрагмент фазового портрета в окрестности неустойчивого фокуса.

Если λ₁= λ₂ ≠ 0 − действительные положительные числа, то точка − узел специального вида − диакритический узел;

при λ₁= λ₂ < 0 − устойчивый диакритический узел;

при λ₁= λ₂ > 0 − неустойчивый диакритический узел.

На рисунке приведен фрагмент фазового портрета в окрестности устойчивого диакритического узла.

Если λ₁= 0, λ₂ ≠ 0, то существует прямая, проходящая через начало координат, все точки которой являются точками покоя.

Если λ₁= λ₂ = 0, то все точки плоскости являются точками покоя системы.

Пример №1

Исследуем характер точки покоя автономной системы

Найдём собственные значения матрицы системы:

Поскольку λ_1,2= ± i √2, то точка покоя − центр.

На рисунках приведены фрагменты фазового портрета и векторного поля в окрестности центра.

4.4.4. Численное интегрирование дифференциальных уравнений первого порядка

4.4.4.1. Задача Коши. Общие замечания. Постановка задачи

Для дифференциального уравнения n-го порядка

. (4.1)

Задача Коши заключается в отыскании решения уравнения (4.1), удовлетворяющего начальным условиям

, (4.2)

где заданные числа. Если функция непрерывна, а ее частные производные ограничены в области, содержащей точку , то существует единственное решение задачи Коши (4.1),(4.2).

Задача Коши для нормальной системы дифференциальных уравнений

(4.3)

заключается в отыскании решения системы (4.3), удовлетворяющего начальным условиям

, (4.4)

где – заданные числа. Если функции непрерывны и имеют ограниченные частные производные в некоторой области, содержащей точку , то существует единственное решение задачи Коши (4.3-4.4).

Известно, что систему дифференциальных уравнений, содержащую производные высших порядков и разрешенную относительно старших производных искомой функции, можно привести к системе вида (4.3) путем введения новых неизвестных функций. В частности, дифференциальное уравнение n-го порядка (4.1) приводится к системе вида (4.3) с помощью замены

,

которая приводит к следующей системе

(4.5)

то есть, к системе n дифференциальных уравнений первого порядка, правая часть которых не зависит от производных искомых функций. Поэтому численные методы решения дифференциальных уравнений традиционно изучают для уравнений первого порядка а затем, как правило, без труда распространяют на нормальные системы дифференциальных уравнений вида (4.3). Так мы и поступим.

Итак, дано дифференциальное уравнение первого порядка, разрешенное относительно производной

(4.6)

и начальное условие

(4.7)

Требуется численно решить задачу Коши (4.6-4.7) на отрезке . Это решение будет состоять в построении таблицы приближенных значений искомого решения в точках , где . Для этого отрезок делят на n равных частей длины , так что величина h называется шагом интегрирования.