4.4.1.2. Фундаментальная матрица решений однородной линейной системы дифференциальных уравнений

Рассмотрим линейную однородную систему обыкновенных дифференциальных уравнений вида

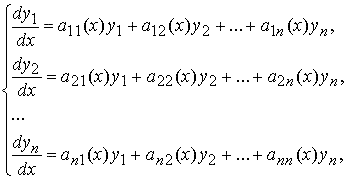
которая в векторной форме записывается в виде

Здесь

Матрица Φ, столбцами которой являются n линейно независимых на [a;b] решений Y₁(x), Y₂(x), ..., Y_n(x) однородной линейной системы Y' = A(x)Y называется фундаментальной матрицей решений системы:

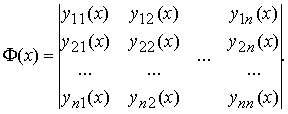
Фундаментальная матрица решений однородной линейной системы Y' = A(x)Y удовлетворяет матричному уравнению Φ' = A(x)Φ.

Здесь

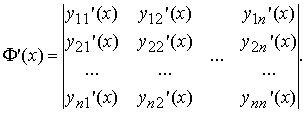
Напомним, что определитель Вронского линейно независимых на [a;b] решений Y₁(x), Y₂(x), ..., Y_n(x) отличен от нуля на [a;b].

У любой однородной линейной системы обыкновенных дифференциальных уравнений существует фундаментальная матрица решений.

Действительно. Пусть Φ₀ − произвольная числовая квадратная матрица с отличным от нуля определителем, det(Φ₀) ≠ 0.

Рассмотрим n решений Y₁(x), Y₂(x), ..., Yn(x) задач Коши вида Y' = A(x)Y, Y(x₀) = Φ₀(j), где Φ0(j) − j-й столбец матрицы Φ, j = 1, 2, ..., n.

Эти решения линейно независимы, т.к. их определитель Вронского отличен от тождественного нуля, W[x₀; Y₁, Y₂, ..., Y_n] = det(Φ₀) ≠ 0.

Матрица Φ(x), столбцами которой являются решения Y₁(x), Y₂(x), ..., Y_n(x) − искомая фундаментальная матрица решений однородной линейной системы дифференциальных уравнений.

Пример №1

Рассмотрим линейную систему обыкновенных дифференциальных уравнений 2-гопорядка:

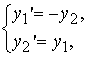
в векторной форме:

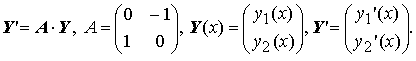
Общее решение этой простой системы нетрудно найти:

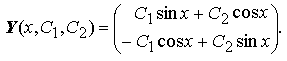
Запишем фундаментальную матрицу решений этой системы.

Рассмотрим пару линейно независимых векторов

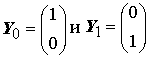
и найдём решения Y⁽¹⁾(x) и Y⁽²⁾(x) двух соответствующих задач Коши:

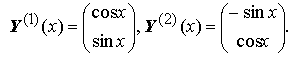
Эти решения линейно независимы всюду, так как их определитель Вронского нигде не обращается в нуль:

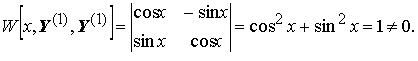
Тогда фундаментальная матрица решений системы:

Легко проверить, что фундаментальная матрица решений удовлетворяет матричному уравнению Φ' = A·Φ:

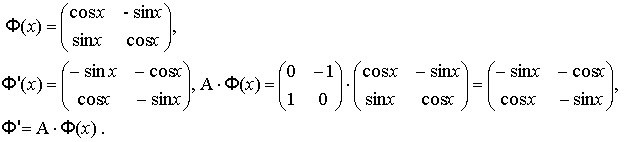
Пример №2

Построим фундаментальную матрицу решений и общее решение линейной системы обыкновенных дифференциальных уравнений 2-гопорядка:

которую удобнее записать в векторной форме:

Найдём собственные значения и собственные векторы матрицы системы:

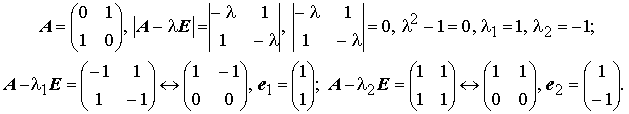
Тогда фундаментальная матрица системы:

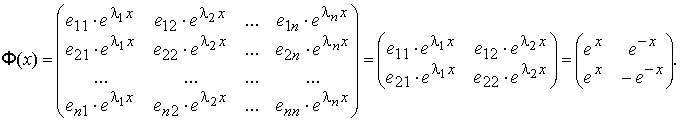
Легко, также, записать общее решение системы:

Правильность решения легко проверить подстановкой в исходную систему.

4.4.1.3. Структура общего решения однородной линейной системы дифференциальных уравнений

Рассмотрим линейную однородную систему обыкновенных дифференциальных уравнений n-го порядка

Здесь

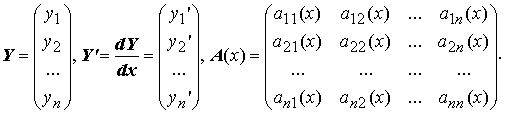
Справедлива следующая теорема о структуре общего решения этой системы.

Если матрица A(x) непрерывна на [a;b], то общее решение системы Y' = A(x)Y имеет вид

Y(x) = Φ(x)·C ≡ C₁·Y₁(x) + C₂·Y₂(x) + ... + C_n· Y_n(x),

где Φ(x) − фундаментальная матрица решений однородной линейной системы, Y₁(x),Y₂(x), ...,Y_n(x) −столбцы этой фундаментальной матрицы решений, C − произвольный постоянный вектор-столбец.

Пример №1

Рассмотрим линейную систему обыкновенных дифференциальных уравнений 2-гопорядка:

которую удобнее записать в векторной форме:

Фундаментальная матрица решений этой системы имеет вид:

Поскольку фундаментальная матрица системы известна, то, опираясь на теорему о структуре общего решения линейной системы ОДУ, можно записать общее решение системы:

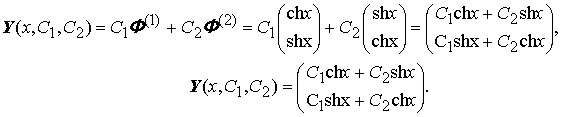
Проверим:

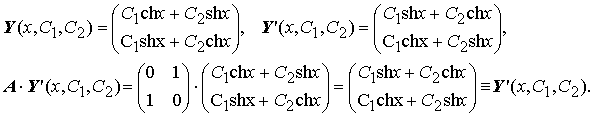
Действительно, построенное нами общее решение удовлетворят системе Y' = A·Y при всех произвольных значениях входящих в выражение общего решения констант.