4.4.2.2. Устойчивость и асимптотическая устойчивость по Ляпунову

Рассмотрим систему дифференциальных уравнений

Полагаем, что выполнены условия теоремы существования и единственности решения задачи Коши.

Пусть некоторое фиксированное решение x = φ(t) этой системы существует при всех t ≥ t₀.

Решение x = φ(t) системы называется асимптотически устойчивым по Ляпунову при t ≥ t₀, если :

− решение x = φ(t) устойчиво по Ляпунову при t ≥ t₀;

− существует такое число Δ > 0, что любое решение x = φ(t), удовлетворяющее условию | x(t₀) − φ(t₀) | < Δ с ростом t стремится к нулю: | x(t₀) − φ(t₀) | → 0 при t → ∞.

Геометрически это означает, что интегральные кривые x = x(t), близкие в момент t = t₀ к интегральной кривой x = φ(t), приближаются к ней с ростом t.

Интегральные кривые и фазовые траектории, отвечающие асимптотически устойчивым решениям, тоже называются асимптотически устойчивыми.

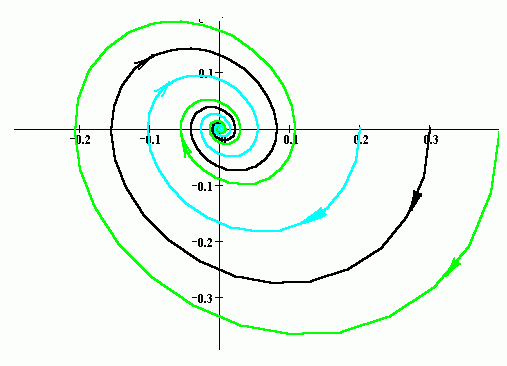
На рисунке чёрным изображена асимптотически устойчивая фазовая траектория, некой системы дифференциальных уравнений второго порядка, которая начинается в точке (0.3, 0), и две, начинающиеся вблизи неё, траектории.

Пример №1

Исследуем на устойчивость решение задачи Коши

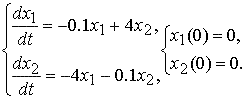
Очевидно, что это решение задачи − тривиальное решение, точка покоя системы, φ(t) = 0,( т.е. φ₁(t) = 0, φ₂(t) = 0).

Докажем, что это нулевое решение асимптотически устойчиво по Ляпунову при t → ∞.

Легко видеть, что решение системы, проходящее через точку (0, x₁(0) , x₂(0)), имеет вид:

Возьмём произвольное ε > 0, δ = ε и исследуем поведение при t → ∞ тех решений x= x(t), которые удовлетворяют условию ‌ x(0) − φ(0) ‌< δ, δ > 0:

Отсюда следует, что тривиальное решение φ(t) ≡ 0 асимптотически устойчиво. На рисунке видно как фазовые кривые устремляются в нуль.

4.4.2.3. Устойчивость положения равновесия линейных систем оду

Рассмотрим линейную систему дифференциальных уравнений n-го порядка:

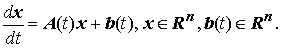
Линейная система устойчива по Ляпунову при t ≥ t₀, если каждое её решение x = φ(t) устойчиво по Ляпунову при t ≥ t₀.

Линейная система асимптотически устойчива по Ляпунову при t → ∞, если каждое её решение x = φ(t) устойчиво по Ляпунову при t → ∞.

Решения линейной системы либо все одновременно устойчивы, либо все неустойчивы. Справедливы следующие утверждения.

Теорема об устойчивости решений линейной системы дифференциальных уравнений: Пусть в неоднородной линейной системе x' = A(t)x + b(t) матрица A(t) и вектор-функция b(t) непрерывны на промежутке [t₀,∞). Система устойчива при t ≥ t₀, тогда и только тогда, когда тривиальное решение x = 0 однородной системы x' = A(t) x устойчиво при t ≥ t₀.

Теорема об асимптотической устойчивости решений линейной системы дифференциальных уравнений: Пусть в неоднородной линейной системе x' = A(t)x + b(t) матрица A(t) и вектор-функция b(t) непрерывны на промежутке [t₀,∞). Система асимптотически устойчива при t → ∞, тогда и только тогда, когда тривиальное решение x = 0 (точка покоя) однородной системы x' = A(t)x асимптотически устойчиво при t → ∞.

Эти утверждения означают, что для исследования устойчивости линейной системы достаточно исследовать устойчивость точки покоя соответствующей однородной системы.

Рассмотрим однородную линейную систему дифференциальных уравнений n-го порядка с постоянной матрицей: x' = A·x .

Исследование такой системы на устойчивость не составляет труда, поскольку справедливы следующие утверждения:

1) Для того чтобы тривиальное решение x ≡ 0 однородной системы x' = A· x было асимптотически устойчиво при t → ∞, необходимо и достаточно, чтобы все собственные значения матрицы A имели отрицательные действительные части.

2) Если собственные значения матрицы A различны, то для устойчивости тривиального решения x ≡ 0 однородной системы x' = A· x необходимо и достаточно, чтобы действительные части всех собственных значений матрицы A были неотрицательны.

3) Если есть хотя бы оно собственное значение матрицы A имеет положительную действительную часть, то тривиальное решение x ≡ 0 однородной системы x' = A· x неустойчиво.

Пример №1

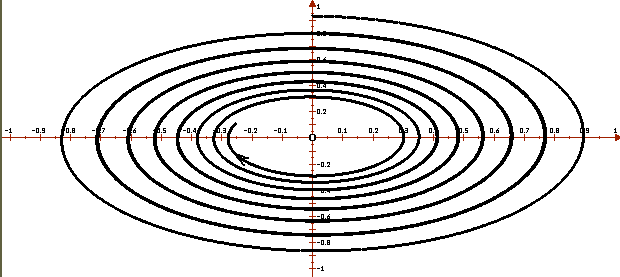
Исследуем на устойчивость линейную систему

Поскольку тривиальное решение, точка покоя системы, φ(t) ≡ 0,( т.е. φ₁(t) ≡ 0, φ₂(t) ≡ 0) устойчиво при t > 0, все решения системы устойчивы, исследуемая система устойчива.

На рисунке изображено несколько фазовых кривых системы (это эллипсы). Видно, что те из них, которые начинаются вблизи нуля, всегда вблизи нуля остаются.

Пример №2

Исследуем на устойчивость линейную систему

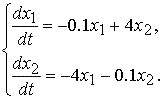
Поскольку тривиальное решение, точка покоя системы, φ(t) = 0,( т.е. φ₁(t) = 0, φ₂(t) = 0) асимптотически устойчиво по Ляпунову при t → ∞, то и все решения системы асимптотически устойчивы. Следовательно исследуемая система асимптотически устойчива.

На рисунке видно, что фазовые кривые, которые начинаются вблизи нуля, устремляются со временем в нуль.