3.5.3. Уравнение Эйлера

Уравнением Эйлера называется однородное дифференциальное уравнение вида

xⁿy⁽ⁿ⁾ + a_n-1x^n-1y^(n-1) + ... + a₁xy' + a₀y = 0.

Коэффициенты a_n-1, ... , a₁, a₀ − постоянные действительные числа.

Если функция y(x) − решение уравнения Эйлера, то функция Cy(x) тоже является решением уравнения.

Уравнение Эйлера заменой x = e^t сводится к однородному линейному уравнению с постоянными коэффициентами.

Выполним замену x = e^t, перейдём к новой переменной t = ln x :

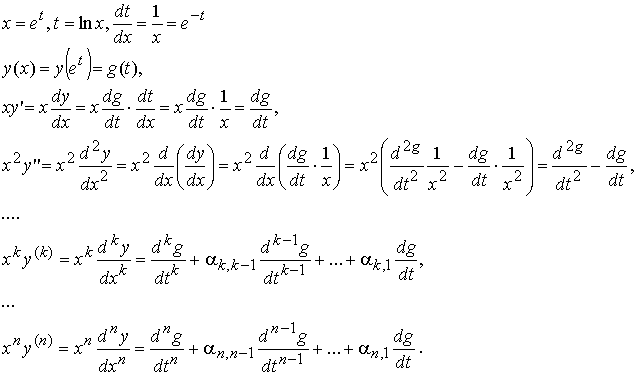
Здесь α_ij − коэффициенты, которые легко вычисляются при последовательном дифференцировании.

После подстановки в уравнение имеем:

Решим это однородное линейное уравнение с постоянными коэффициентами − его общее решение g = g(t,C₁, C₂, ... ,C_n). Вернувшись к переменной x, получим общее решение уравнения Эйлера: y(x,C₁, C₂, ... ,C_n) = g(lnx,C₁, C₂, ..., C_n).

Пример №1

Найдём общее решение уравнения Эйлера x²y^'' + 3xy' + y = 0.

Выполним замену x = e^t, перейдём к новой переменной t = ln x:

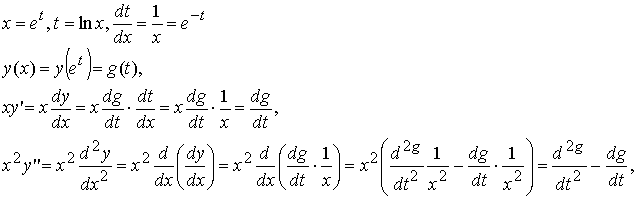
После подстановки в уравнение имеем: 2g'' + 2g' + g = 0.

Составим и решим характеристическое уравнение:

2λ² + 2 λ +1 =0, λ₁ = λ₂ = −1.

Фундаментальную систему решений однородного уравнения образуют функции e^-t и te^-t, а общее решение g(t,C₁, C₂) = C₁e^−t + C₂t e^−t.

Вернувшись к переменной x, t = ln x, получим общее решение уравнения Эйлера: y(x,C₁, C₂) = C₁e^−lnx + C₂lnx e^−lnx,

y(x,C₁, C₂) = C₁x⁻¹ + C₂lnx ⁻¹ .

4. Системы дифференциальных уравнений

4.1. Системы обыкновенных дифференциальных уравнений. Основные понятия

Рассмотрим систему обыкновенных дифференциальных уравнений n-го порядка

или

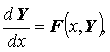
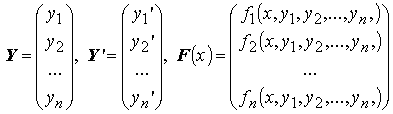
Задачей Коши для этой системы называется следующая задача:

найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x₀)=Y₀, где Y₀ − некоторый постоянный вектор.

Вектор-функция Y = Y(x,С), зависящая от произвольного вектора С, называется общим решением системы, если:

− при любом векторе C, вектор-функция Y(x,С) является решением системы;

− какова бы ни была начальная точка ((x₀, Y₀), существует такой вектор С⁽⁰⁾, что Y(x⁽⁰⁾,С⁽⁰⁾) = Y₀.

Пример №1

Дана система обыкновенных дифференциальных уравнений 4-го порядка относительно двух неизвестных функций x = x(t) и y = y(t):

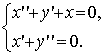
Она может быть записана в канонической форме:

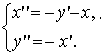
Обозначив x(t) = z₁(t), y(t) = z₂(t), x'(t) = z₃(t), y'(t) = z₄(t), можно записать систему в нормальной форме:

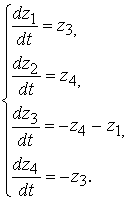
И, безусловно, удобнее всего записывать систему в векторной форме:

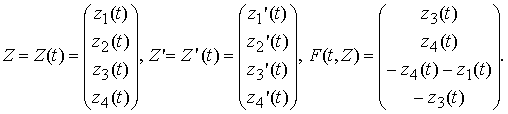
4.2. Фазовое пространство. Фазовые траектории

Рассмотрим систему обыкновенных дифференциальных уравнений n-го порядка Y ' = F(x,Y), и пусть вектор-функция Y = Φ(x) − решение системы, определённое на промежутке [a;b].

Множество точек Φ(x), x∈ [a;b] − кривая в пространстве R_Yⁿ. Эту кривую называют фазовой траекторией системы (или просто траекторией, или фазовой кривой), а пространство R_Yⁿ, в котором расположены фазовые траектории, называют фазовым пространством системы.

Интегральная кривая системы определяется уравнением Y = Φ(x), x∈ [a:b], и изображается в (n +1)-мерном пространстве R_{Y, x}ⁿ⁺¹.

Фазовая траектория − это проекция интегральной кривой на пространство R_Yⁿ.

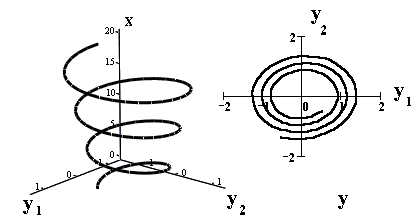
На рисунке изображена интегральная кривая в пространстве R_{Y, x}²⁺¹ и фазовая траектория в пространстве R_Y²:

Пример №1

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений 2-го порядка, записанную в нормальной и в векторной форме

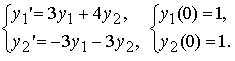
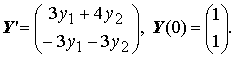
Решение этой задачи можно также записать в обычной аналитической и в векторной форме:

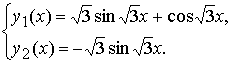
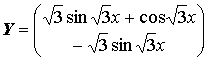
На рисунке приведены изображения соответствующей интегральной кривой, расположенной в пространстве R_{Y, x}²⁺¹, и фазовой траектории, расположенной в пространстве R_Y²: