3.1.2. Уравнения, не содержащие независимой переменной

F(y, y', ..., y⁽ⁿ⁾) = 0

Если в результате каких–либо преобразований порядок n уравнения F(x, y, y ',..., y⁽ⁿ⁾) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие независимой переменной – уравнения вида F(y, y', ..., y⁽ⁿ⁾) = 0.

Порядок уравнения можно понизить, заменив y ' = p(y).

После подстановки получим дифференциальное уравнение относительно функции p = p(y) , в котором порядок старшей производной от p(y) будет на единицу меньше, чем порядок старшей производной от y(x) в исходном уравнении.

Выполним в уравнении F(y, y', ..., y⁽ⁿ⁾) = 0 замену y ' = p(y).

Для этого выразим через p(y), входящие в уравнение производные искомой функции y = y (x):

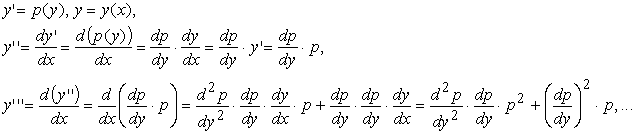
Понятно, что производная k-го порядка функции y (x) выражается через производные не старше (k-1)-го порядка от функции p(y).

Это означает, что после такой подстановки в исходное уравнение получим дифференциальное уравнение относительно функции p = p(y) , в котором порядок старшей производной от p(y) будет на единицу меньше, чем порядок старшей производной от y(x) в исходном уравнении:

F(y, p , p', ..., p^{(n - 1)}) = 0.

Пример №1

Решим задачу Коши

y'' = 2y³, y(0)=1, y'(0) = 1.

Обозначим y ' = p(y). Тогда

и

Подставив, получим задачу Коши для уравнения первого порядка относительно p(y):

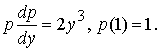
Это уравнение с разделяющимися переменными, которое легко интегрируется:

константу определим из начального условия,

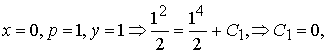
и поскольку p(1) = 1 > 0, имеем

Имеем ещё одно уравнение 1-го порядка с разделяющимися переменными y' = y², y(0)=1, которое также нетрудно решить:

3.1.3. Уравнения, не содержащие искомой функции

F(x, y', ..., y⁽ⁿ⁾) = 0

Если в результате каких–либо преобразований порядок n уравнения F(x, y,y',..., y⁽ⁿ⁾ ) = 0 может быть понижен, то говорят, что уравнение допускает понижение порядка.

К уравнениям, допускающим понижение порядка, относятся уравнения, не содержащие искомой функции – уравнения вида F(x, y', ..., y⁽ⁿ⁾) = 0.

Порядок уравнения можно понизить, заменив y ' = p(x).

После подстановки получим дифференциальное уравнение относительно функции p = p(x) на единицу меньшего порядка, чем исходное уравнение:

F(x, p, p', ..., p^{(n - 1)}) = 0.

Выполним в уравнении F(y, y', ..., y⁽ⁿ⁾) = 0 замену y '= p(x).

Для этого выразим через p(x), входящие в уравнение производные искомой функции y = y (x):

y ' = p(x), y'' = p'(x), ..., y^(k)= p^(k-1)(x).

После такой подстановки получим уравнение на единицу меньшего порядка:

F(x, p, p', ..., p^(n-1)) = 0.

Пример №1

Решим уравнение

2xy'y'' = (y')² − 1.

Обозначим y ' = p(x). Тогда y '' = p'(x) и после подстановки в исходное уравнение получаем уравнение первого порядка с разделяющимися переменными

2xpp' = (p)² − 1.

Решаем полученное уравнение 1-го порядка:

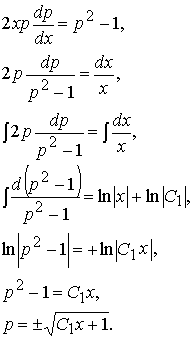
Имеем пару уравнений 1-го порядка с разделяющимися переменными

решения которых легко получаем интегрированием: