4.4.4.2. Метод Эйлера

Будем считать, что шаг интегрирования h настолько мал, что для всех значения искомой функции мало отличается от . Тогда для можно написать

Иными словами, на этом участке интегрирования кривая заменяется отрезком касательной к ней в точке .

Для получим

Аналогично, для получим

Продолжая строить значения приближенного решения по тому же закону, получим

Используя известные обозначения, схему метода Эйлера можно представить формулами:

(4.8)

Рис. 4.1.

Геометрический смысл метода Эйлера заключается в том, что искомая интегральная кривая заменяется ломаной, соединяющей точки (рис. 4.1). Причем первое звено ломаной касается истинной интегральной кривой в точке . Эта ломаная называется ломаной Эйлера. При последовательность ломаных Эйлера на отрезке стремится к искомой интегральной кривой.

Оценку точности метода Эйлера, если неизвестно точное решение , проводят с помощью двойного пересчета – с шагом h и с шагом .

Совпадение десятичных знаков в полученных двумя способами результатах дает основание считать их верными.

Метод Эйлера легко распространяется на системы дифференциальных уравнений (4.3) и на дифференциальные уравнения высших порядков (4.1), которые должны быть предварительно приведены к нормальной системе (переход от (4.1) к (4.5)).

Рассмотрим систему двух дифференциальных уравнений первого порядка:

(4.9)

c начальными условиями . Приближенные значения и вычисляются последовательно по формулам:

(4.10)

4.4.4.3. Модифицированный метод Эйлера

Рассматриваемый метод является более точным методом по сравнению с предыдущим. Модификация метода направлена на то, чтобы точно определить направление перехода из точки в точку . Для чего производятся дополнительные промежуточные вычисления, в результате которых определяются координаты промежуточной точки

(4.11)

с помощью которых и определяется следующее приближенное значение искомого решения по формуле

(4.12)

Геометрический смысл модифицированного метода Эйлера показан на рис. 4.2. Исходя из точки , получаем по методу Эйлера для точку . Для , применяя метод Эйлера, получили бы точку , находящуюся на касательной к интегральной кривой в точке . Модифицированный метод состоит в том, что из точки проводится отрезок , параллельный отрезку , направленному в соответствии со значением углового коэффициента в точке . Точка , которая получена по модифицированному методу Эйлера, находится ближе к истинной кривой, чем точка . Следовательно, модифицированный метод Эйлера будет обеспечивать большую точность, чем метод Эйлера при одном и том же числе n разбиения отрезка интегрирования

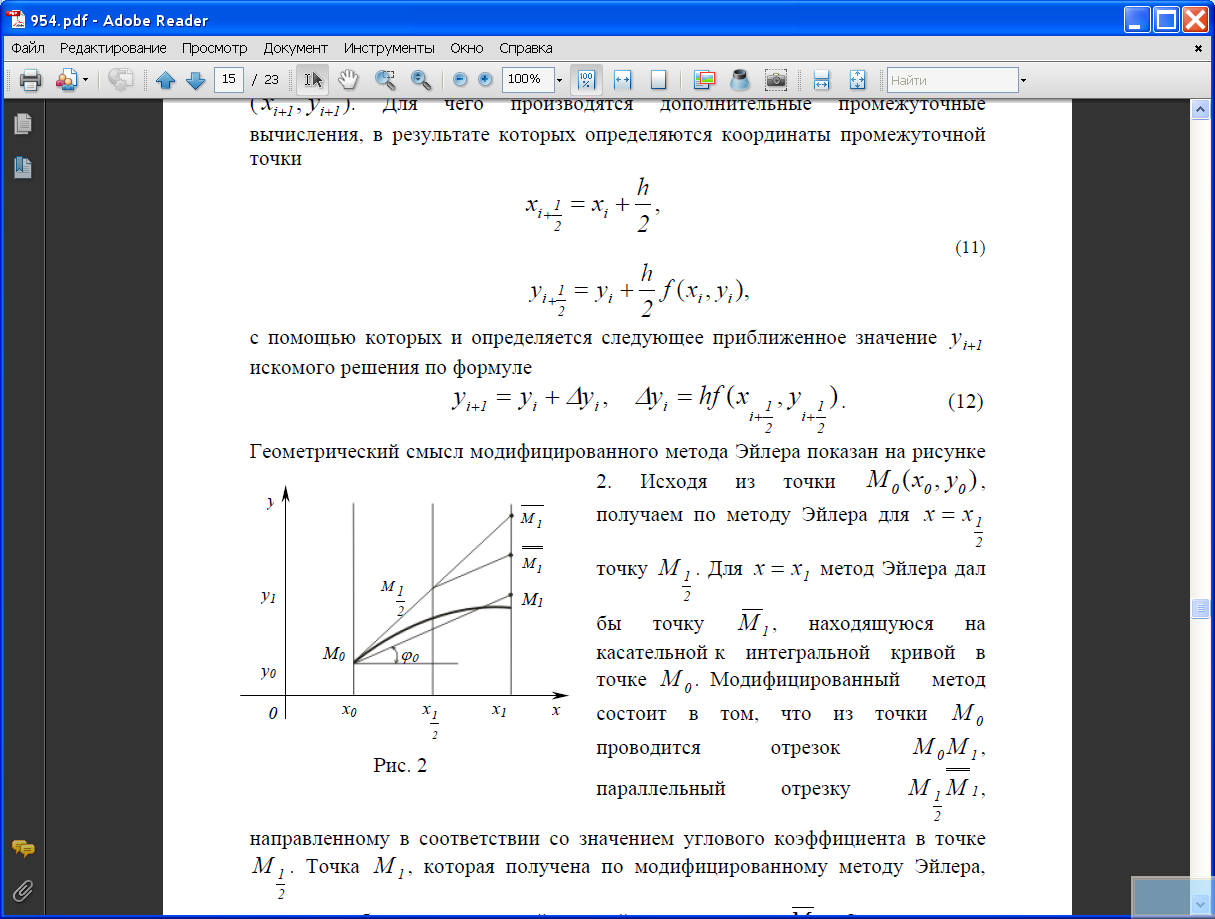
Рис. 4.2.

Модифицированный метод Эйлера можно легко распространить на нормальную систему дифференциальных уравнений (4.3). Рассмотрим систему двух уравнений первого порядка:

с начальными условиями .

Приближенные значения , вычисляются последовательно по формулам:

(4.13)

где