
Бутырин Алексейчик Сборник задач по ТОЭ т1
.pdf
(векторами), поэтому несимметричная система трех векторов на комплексной плоскости может быть представлена суммой трех симметричных систем векторов. Фазные напряжения трехфазной системы могут быть представлены выражением:
U |
A |
= U |
1 |
+ U |
2 |
+ U |
0 |
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
B |
= a2U |
1 |
+ aU |
2 |
+ U |
0 |
, |
|
(4.11) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
= aU |
|
+ a2U |
|
+ U |
|
, |
|
||||||
|
C |
|
|
1 |
|
|
|
|
2 |
|
|
0 |
|
|
|
где а и а2 являются фазными множителями, равными а = ej120, а2 = ej240,
причем а + а2 + 1 = 0. На рис. 4.10 дано геометрическое представление несимметричной системы векторов A, B, C. Преобразовав представленную систему (4.11), можно найти значения составляющих
U1 , U2 , U0 :
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
), |
|
U |
1 |
= -- |
(U |
A |
+ aU |
B |
+ a |
U |
C |
|
||||
|
3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
U |
2 |
= --(U |
A |
+ a |
U |
B |
+ aU |
C |
), |
(4.12) |
||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ UB + UC). |
|
|
|
|||||||
U0 = --(UA |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
Каждой последовательности на участке цепи соответствуют свои сопротивления, которые удовлетворяют соотношениям:
|
|
|
|
|
|
|
U1 |
|
|
|
|
|
|
U2 |
|
|
U |
0 |
|
|
|
|
||||||
|
|
|
|
|
|
Z1 |
= ------ , Z2 = ------ , Z0 |
= |
------ , |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
I 1 |
|
|
|
|
|
|
I 2 |
|
|
I 0 |
|
|
|
||||||||
|
|
A |
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
A0 B0 |
C |
0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
2 |
|
|||
|
|
= |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
|
|
||||||||||
C |
C |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
B |
|
A = |
A |
1 + A2 + A0, |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
B = B1 + B2 + B0, |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
C |
= |
C |
1 + |
C |
2 + C |
0. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Рис. 4.10 |
|
|
|
|
|
|
|
|
|
|
|||||||||
171

где U1 , U2 , U0 — напряжения прямой, обратной и нулевой последовательности на участке цепи; I 1 , I 2 , I 0 — токи прямой, обратной
и нулевой последовательности. Значения сопротивлений последовательностей зависят от конкретных элементов участка цепи.
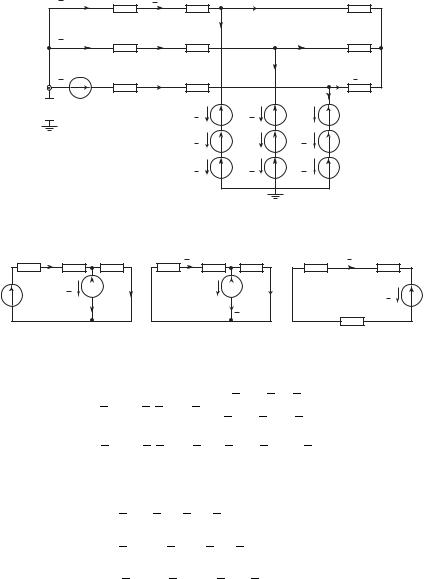
Составление схем прямой, обратной и нулевой последовательности. Для расчета по методу симметричных составляющих обычно пользуются однофазными схемами замещения для каждой последовательности. Рассмотрим порядок составления этих схем на примере цепи на рис. 4.11.
Генератор имеет синусоидальную ЭДС Ег и характеризуется сопротивлениями различной последовательности: Zг1, Zг2, Zг0, — сопротивления прямой, обратной и нулевой последовательности. Линия и двигатель также имеют различные сопротивления для последовательностей: Zл1, Zл2, Zл0 — для линии; Zдв1, Zдв2, Zдв0 — для двигателя.
Схема замещения с учетом замены несимметрии на последовательности приведена на рис. 4.12.
Эквивалентные схемы для расчета прямой, обратной и нулевой последовательностей представлены на рис. 4.13, 4.14, 4.15.
Уравнения, описывающие однофазные схемы замещения цепи.
Для схем на рис. 4.13, 4.14, 4.15 составляются уравнения относительно U1, I1, U2, I2, U0, I0:
|
|
|
|
|
|
|
EгZдв1 |
|
|
|
|
|
|
(Zг1 + Zл1)Zдв1 |
|
||||||||
U1 = E1 – Z1I 1 , E1 |
= ---------------------------------------- |
|
|
|
|
|
, Z1 |
= |
---------------------------------------- |
|
|
|
|
|
; |
||||||||
|
|
|
|
|
Zг1 |
+ Zл1 |
+ Zдв1 |
|
|
|
|
|
|
Zг1 |
+ Zл1 |
+ Zдв1 |
|
||||||
|
|
|
|
Генератор |
Линия |
|
|
|
|
|
Двигатель |
|
|
||||||||||
|
|
|
EA |
|
Zг |
A |
|
Zл |
|
|
|
|
|
|
Zдв |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EB |
|
Zг |
B |
|
Zл |
|
|
|
|
|
|
Zдв |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EC |
|
Zг |
C |
|
Zл |
|
|
|
|
|
|
|
Z |
дв |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
172
EA
EB
EC
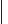
 ZN
ZN
Zг
Zг
Zг
IA г
IB г
IC г
Zл |
IA дв |
|
|
|
Zдв |
||
Zл |
IA |
|
IB дв |
|
Zдв |
||
|
|
|
|||||
Zл |
|
|
IB |
|
IC дв |
Zдв |
|
|
|
|
|
||||
|
|
a2U |
|
|
|
IC |
|
U |
1 |
1 |
aU |
1 |
|
|
|
|
|
|
|
|
|||
U |
2 |
aU |
2 |
a2U |
2 |
|
|
|
|
|
|
|
|||
U0 |
U0 |
U0 |
|
|
|||
Рис. 4.12
Zг1 |
Iг1 |
Zл1 |
Zдв1 |
Zг2 |
Iг2 |
Zл2 |
Zдв2 |
Zг0 |
I0 |
Zл0 |
Eг |
|
U1 |
Iдв1 |
|
|
U2 |
Iдв2 |
|
|
U0 |
|
|
|
|
|
|
3ZN |
||||
|
|
|
I1 |
|
|
|
I2 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.13 |
|
Рис. 4.14 |
|
|
Рис. 4.15 |
|||
|
|
|
(Zг2 |
+ Zл2)Zдв2 |
|
|
|
|
U2 |
= –Z2I 2 |
, Z2 |
= ---------------------------------------- |
|
|
; |
|
|
|
|
|
Zг2 |
+ Zл2 + Zдв2 |
|
|
|
|
U0 = –Z0I 0 , Z0 = Zг0 + Zл0 + 3ZN .
Дополнительные уравнения для данной несимметрии (граничные условия):
I A = I 1 + I 2 + I 0 = 0,
I |
B |
= a2I |
1 |
+ aI |
2 |
+ I |
0 |
= 0, . |
|
|
|
|
|
2
UC = aU1 + a U2 + U0 = 0.
Из полученной системы шести уравнений находятся неизвестные
U1, I1, U2, I2, U0, I0.
Вид дополнительных уравнений определяется конкретным видом несимметрии (см. приведенные решения задач).
173
Несинусоидальные токи в трехфазных цепях
В трехфазных цепях с симметричными источниками кроме реактивных сопротивлений, зависящих от частоты, необходимо учитывать изменения гармонических составляющих напряжений источников от частоты. Пусть ЭДС фазы А изменяется по закону
eA = Em sinωt + E3m sin3ωt + E5m sin5ωt + … + Ekm sinkωt. (4.13)
В выражении eA(t) не представлены четные гармоники, так как
большая часть трехфазных источников представляют собой синхронные генераторы (или вторичные обмотки трансформаторов). Оба эти устройства в силу симметричности кривых намагничивания магнитопроводов не содержат на выходе четных гармоник. В трехфазных цепях, где источниками являются электронные устройства (инверторы, преобразователи и т.д.), четные гармоники содержатся в напряжении источников. ЭДС в других фазах записываются с учетом пространственного сдвига обмоток на 120°, который при вращении магнитного поля с частотой ω соответствует временному′ запаздыванию на t – T/3 или t – 2T/3:
|
e |
|
= E |
|
sin ω |
|
t |
– |
T |
|
|
|
|
|
sin 3ω |
|
T |
+ E |
|
|
|
sin 5ω |
|
t – |
T |
+ … |
|||||||||||||
|
|
|
|
-- + E |
|
|
|
|
t – -- |
|
|
|
|
-- |
|||||||||||||||||||||||||
|
|
B |
|
|
1m |
|
|
|
|
|
|
|
3 |
|
|
3m |
|
|
|
|
|
|
3 |
|
|
|
5m |
|
|
|
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
… + E |
|
sin kω |
|
t – |
T |
= E |
|
|
|
sin |
|
|
|
2π |
+ E |
|
|
sin (3ωt – 2π) + |
||||||||||||||||||||
|
|
|
-- |
|
|
|
|
|
ωt – ------ |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
km |
|
|
|
|
|
|
|
|
3 |
|
|
|
1m |
|
|
|
|
|
3 |
|
|
|
|
3m |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
sin |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
sin k |
|
|
k |
|
|
|
|
||||||||
|
|
|
|
|
+ |
E |
|
|
5 |
ωt – --2π |
+ … + E |
|
ωt – --2π ; |
|
(4.14) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
5m |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
km |
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
e |
|
=E |
|
sin ω |
|
t |
|
2T |
+ E |
|
|
sin |
3ω |
|
t |
2T |
+ E |
|
|
|
sin 5ω |
|
t – |
2T |
|||||||||||||||
C |
|
|
– ------ |
|
|
|
|
– ------ |
|
|
|
|
------ |
+ … |
|||||||||||||||||||||||||
|
|
|
1m |
|
|
|
|
|
|
3 |
|
|
|
3m |
|
|
|
|
|
|
|
3 |
|
|
|
5m |
|
|
|
|
3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
… + E |
|
sin kω |
|
t – |
2T |
= E |
|
|
sin |
|
|
|
|
4π |
+ E |
|
|
sin (3ωt – 4π) + |
||||||||||||||||||||
|
|
|
------ |
|
|
|
|
|
|
ωt – ------ |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
km |
|
|
|
|
|
|
|
|
3 |
|
|
|
1m |
|
|
|
|
|
3 |
|
|
|
|
3m |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
+ E |
|
|
sin |
|
5 |
|
|
20 |
|
|
+ … + E |
|
sin |
|
|
|
|
k |
|
|
|
(4.15) |
||||||||||||
|
|
|
|
|
|
|
|
ωt – ----- |
π |
|
|
|
kωt – --4π . |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
5m |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
km |
|
|
|
|
|
|
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из выражений (4.13), (4.14) и (4.15) для eA(t), eB(t), eC(t) можно
сделать вывод, что гармоники 1, 7, 13, …, (3n + 1) обладают свойствами прямой последовательности, гармоники, кратные трем (3, 9, 15, …, 3(2n – 1)), обладают свойствами нулевой последовательности, гармоники 5, 11, 17, …, (6n – 1)) обладают свойствами обратной последовательности.
174
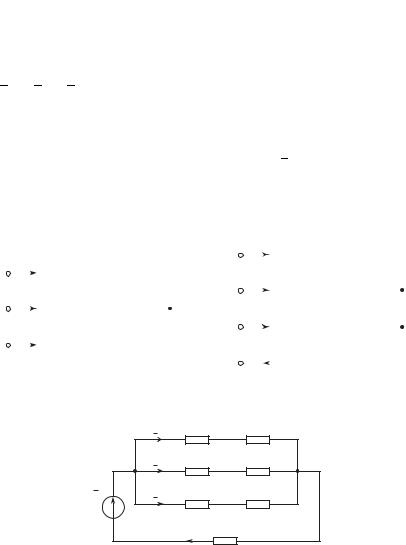
Расчет проводится по методу наложения. Для каждой гармоники рассматривается эквивалентная схема с учетом частоты и последовательности. При соединении нагрузки звездой (рис. 4.16) без нейтрального провода линейные токи содержат только гармоники прямой и обратной последовательности, т.е. k = 3n + 1 и k = 6n – 1, и не содержат гармоники, кратные трем. Напряжение смещения при симметричной нагрузке (ZA = ZB = ZC ) содержит только гармоники,
кратные трем, т.е. k = 3(2n – 1). Кроме того, линейные напряжения не содержат гармоник, кратных трем. При соединении нагрузки звездой с нулевым проводом (рис. 4.17) токи в линейных проводах содержат составляющие всех гармоник. При симметричной нагрузке (ZA = ZB = ZC ) в нулевом проводе отсутствуют токи прямой и обрат-
ной последовательности, т.е. гармоники k = 3n + 1 и k = 6n – 1.
Для расчета токов нулевой последовательности исходную схему преобразуют в эквивалентную (рис. 4.18). В фазах цепи токи гармоник k = 3(2n – 1) равны и в 3 раза меньше тока I N(k) .
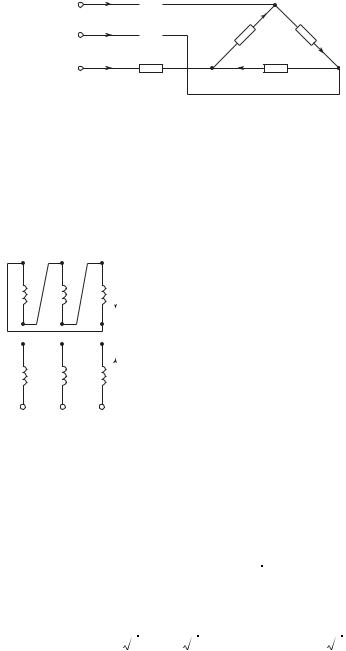
При соединении нагрузки треугольником (рис. 4.19) фазные и линейные токи не содержат гармоник, кратных трем, т.е. k = 3(2n – 1).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
A(k) |
Zл(k) |
|
ZA(k) |
|||
A |
IA(k) |
Zл(k) |
|
|
Z |
A(k) |
A |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
B |
|
|
|
IB(k) |
Zл(k) |
|
ZB(k) |
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
B |
|
|
IB(k) |
Zл(k) |
|
|
Z |
B(k) |
N |
|
|
|
|
N |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
C |
|
|
IC(k) |
Zл(k) |
|
Z |
C(k) |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
C |
|
IC(k) |
Zл(k) |
|
Z |
C(k) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
N |
|
I |
N(k) |
ZN(k) |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 4.16
Рис. 4.17
|
IA(k) |
|
Zл(k) |
ZA(k) |
|
IB(k) |
|
Zл(k) |
ZB(k) |
E(k) |
IC(k) |
|
Zл(k) |
ZC(k) |
|
|
|||
|
|
I |
N(k) |
ZN(k) |
|
|
|
|
|
|
|
Рис. 4.18 |
||
175
A |
IA(k) |
Zл(k) |
|
a |
|
|
|
|
|
|
|
Ica(k) |
|
B |
IB(k) |
Zл(k) |
Zca(k) |
Zab(k) |
||
|
|
|
|
|||
C |
IC(k) |
Zл(k) |
c |
Ibc(k) |
Iab(k) |
b |
|
|
|
|
|
Zbc(k) |
|
Рис. 4.19
После расчета комплексным методом всех гармоник находят по принципу наложения мгновенные значения напряжений и токов.
4.1. ТРЕХФАЗНЫЕ ИСТОЧНИКИ И ТРАНСФОРМАТОРЫ,
СОЕДИНЕНИЯ ОБМОТОК
A |
B |
C |
|
|
|
|
|
4.1(р). На щиток трехфазного трансфор- |
|||||
|
|
|
|
|
|
|
|
|
|
|
матора 660/380 В мощностью 40 кВæA |
||
|
|
|
|
|
|
|
U |
|
|
выведены три пары зажимов его вторич- |
|||
|
|
|
|
|
|
|
|
1ф |
|
|
|
||
|
|
|
|
|
|
|
|
ной обмотки (зажимы 1—4, 2—5, 3—6). |
|||||
|
|
|
|
|
|
|
|
|
|
|
Максимальное |
напряжение |
вторичной |
|
|
|
|
|
|
|
|
|
|
|
обмотки не может превышать 220 В, а пер- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
5 |
6 |
|
|
|
|
|
|
|
вичной — 660 В (рис. к задаче 4.1(р)). |
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
U |
|
Нарисовать схему соединений обмоток |
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2ф |
трансформатора, определить токи первич- |
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
ной и вторичной обмоток в номинальном |
||
|
|
|
|
|
|
|
|
|
|
|
|||
a |
b |
c |
|
|
|
|
|
режиме. Потерями в трансформаторе пре- |
|||||
1 |
2 |
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
небречь. |
|
|
Рис. к задаче 4.1(p) |
|
|
|
|
|
Решение. На щитке, если нет уточне- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
ний, указывают |
линейные |
напряжения. |
Обмотки трансформатора могут иметь два варианта соединения: а) треугольник — звезда, б) звезда — звезда.
Вариант а). Фазное напряжение первичной обмотки
U1ф ≤ 660 В (U1л = U1ф).
Фазное напряжение вторичной обмотки
U2ф ≤ 220 В (U2л = 
 3 U2ф).
3 U2ф).
Токи равны:
|
|
S |
|
40æ103 |
|
35 |
|
I1л |
= -------- |
-------- |
= |
-------3--------------æ660 |
= 35 А, I1ф = |
------ |
= 20,2 А, |
|
|
3U1л |
|
|
3 |
|
176
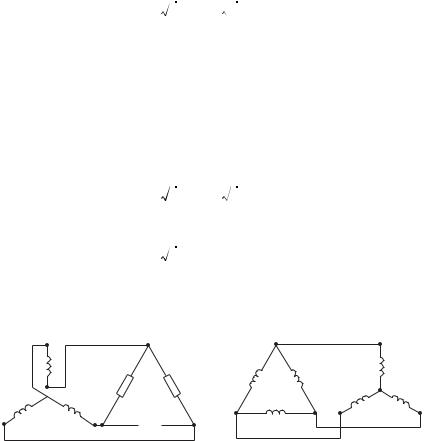
|
S |
|
40æ10 |
3 |
I2л = I2ф = -------- |
--------- |
= |
--------------------- |
= 60,6 А. |
|
3U2л |
|
3æ380 |
|
Вариант б). Фазное напряжение первичной обмотки
U1ф = 380 В, U1л = 660 В.
Фазное напряжение вторичной обмотки
U2ф = 220 В, U2л = 380 В.
Токи:
|
|
S |
|
40æ10 |
3 |
I1л = I1ф |
= |
-- ------ --------- |
= |
--------------------- |
= 35 А, |
|
|
3 U 1 л |
|
3æ660 |
|
|
|
40 æ 10 |
3 |
|
|
I2л = I2ф |
= --------------------- |
3 æ 380 |
= 60,6 А. |
||
4.2. Фазное напряжение трансформатора 220 В. Одна его фаза включена неправильно (рис. к задаче 4.2).
A A
X R R
 Y
Y
Z
C B
C B R
|
|
|
Рис. к задаче 4.2 |
Рис. 1 к задаче 4.3(p) |
|
Найти фазные токи и напряжения на приемнике при активной нагрузке R = 10 Ом.
4.3(р). Три однофазных трансформатора питают электродвигатель, потребляющий мощность 300 кВт при cosϕ = 0,8. Напряжение UАВ = UВС = UСА = 3 кВ.
Определить токи в проводах линии, активную и реактивную мощности, отдаваемые каждым трансформатором:
в исходной схеме (рис. 1 к задаче 4.3(р)); при отсутствии трансформатора в фазе СВ (рис. 2 к задаче 4.3(р)).
177

A |
IA |
UCA |
UAB |
C
 B
B  IB
IB
IC
Рис. 2 к задаче 4.3(p)
Решение. В исходной схеме имеем UАВ = 3000 0 В, UВС = = 3000 –120° В, UСА = 3000 120° В. Фазное напряжение UА =
UAB
=----------1 –30° . Режим симметричный, поэтому токи в фазах одина-

 3
3
300æ103 = ----------------------------------------- = 72,75 А.

 3æ3æ103æ0,8
3æ3æ103æ0,8
Обмотки трансформаторов находятся в одинаковых условиях, поэтому РАВ = РВС = РСА = 300/3 = 100 кВт, QАВ = QВС = QСА = P tgϕ = = 100 tg36,86° = 75 квар.
Если обмотка ВС отсутствует, токи IA, IВ, IС не изменяются, так как не меняются потенциалы точек А, В, С. Токи IA = 72,25 (–30° – ϕ) = = 72,25 –66,86° А, IВ = 72,25 –186,86° А, IС = 72,25 53,14° А.
Мощность
*
SAB = UAB(–I B) = 3000(–72,25 186,86°) = 215 198 + j25 890 ВæА,
РАВ ≈ 215,2 кВт, QАВ ≈ 25,9 квар,
*
SCA = UCA(–I C) = 3000 120°(72,25 –53,14°) = 85 178 + j199 311 ВæА,
РCA ≈ 85,1 кВт, QCA ≈ 199,3 квар.
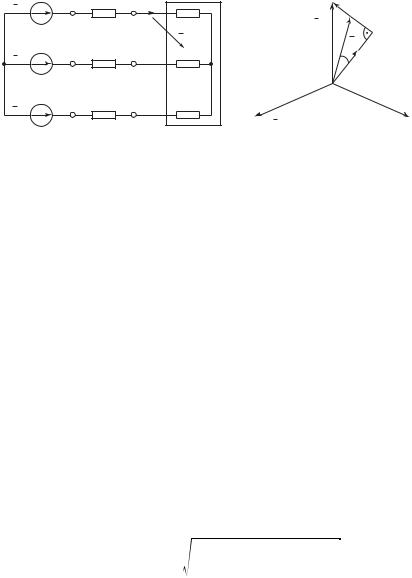
4.4(р). Каждая фаза трехфазного синхронного генератора, обмотки которого соединены звездой (рис. 1 к задаче 4.4(р)), имеет индуктивное сопротивление 5 Ом и ничтожное сравнительно с ним активное сопротивление. ЭДС каждой фазы генератора 4500 В.
Определить линейное напряжение на зажимах генератора при мощности нагрузки 1,5 МВт с cosϕ = 0,8 (ϕ > 0).
178
Eг A |
A |
Zг |
A |
IA |
Нагрузка |
A |
ZгIA |
|
|
|
|
||||||||
|
|
|
|
|
|
Eг A |
|
A |
|
|
|
|
|
|
UA |
|
U |
A |
K |
|
|
|
|
|
|
|
|
|
|
Eг B |
B |
Zг |
B |
|
|
|
|
|
|
N |
|
|
|
|
|
|
IA |
|
|
Eг C |
|
Zг |
|
|
|
N |
|
|
|
C |
C |
|
|
C |
|
|
B |
||
|
|
|
|
|
|
Eг C |
|
|
Eг B |
|
|
|
|
|
Нагрузка |
|
|
|
|
Рис. 1 к задаче 4.4(p) |
Рис. 2 к задаче 4.4(p) |
Решение. Из условия задачи ЕгА = 4500 В, Р = 1,5æ106 Вт, cosϕ = 0,8,
sinϕ = 0,6.
Векторная диаграмма для фазы А имеет вид, показанный на рис. 2 к задаче 4.4(р).
Из треугольника А′KN определяем:
А′N2 = (А′K)2 + (NK)2 или E2 |
= (Z |
|
I |
|
|
+ U |
|
sin ϕ)2 + U2 |
cos2ϕ , |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
г |
|
г |
|
|
A |
|
A |
|
|
|
|
|
|
A |
|
|||
Eг2 = (5IA + 0,6UA)2 + 0,82UA2 , P = 3UАIА cosϕ, IA = |
----------------------- |
|
|
P . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3UAæ0,8 |
|||
После подстановки численных значений получаем: |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
5æ1,5æ10 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||||||
|
4500 |
|
= ----------------------------- |
3UAæ0,8 |
+ U |
A |
æ0,6 |
|
+ U |
A |
æ0,8 |
|
; |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3,125æ10 |
6 |
2 |
|
2æ5æ1,5æ0,6æ |
|
|
6 |
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
10 |
|
|
|
2 |
|
||||||||||||||||
|
4500 |
|
= -------------------------- |
|
|
|
|
|
+ |
------------------------------------------------- |
|
|
|
|
|
3æ0,8 |
|
|
|
+ |
U |
A |
; |
|||||
|
|
|
|
|
|
|
UA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
U4 |
– (45002 – 3,75æ106)U2 |
|
+ 9,76æ106 = 0 ; |
|
|
||||||||||||||||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U4 |
– 16,5æ106U2 + 9,76æ106 = 0 . |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
A |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решаем биквадратное уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
= 16,5æ10 |
6 |
|
|
16,5æ |
|
6 |
2 |
|
|
|
|
|
|
|
|
|
||||||||
|
U2 |
|
|
|
± |
|
10 |
|
– 9,76æ106 , |
|
||||||||||||||||||
|
A |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U2 |
= 16,5-----------------------æ106 |
+ |
7,63æ106 = 15,88æ106 |
В2, U |
|
|
= 3,98æ103 В, |
|||||||||||||||||||||
A |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
U2 = 16,5-----------------------æ106 |
– 7,63æ106 = 0,62æ106 В2, U |
|
= 787 В. |
||||||||||||||||||||||||
|
A |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
179

Решение для UA возможно, если угол между ЕгА и IА стремится к
2
90°. Обычно этот угол близок к ϕ, поэтому выбираем UA = 3980 В.
1
Линейное напряжение Uл = UAB = 
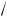 3UA =
3UA = 
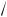 3æ3980 = 6885 В.
3æ3980 = 6885 В.
1
4.5(р). Фазные обмотки генератора соединены треугольником. Чему равны токи фаз, если приемник отсоединен, а система фаз-
ных ЭДС симметрична?
Решение. Токи фаз генератора равны нулю. По закону Кирхгофа имеем 3ZфI ф = EAB + EBC + ECA = 0 , следовательно, Iф = 0.
4.6. Какие из многофазных систем токов являются симметричными:
1) i1 = 20 2 sinωt А, i2 = 20 |
2π |
|
|
2π |
2 sin(ωt – ------ ) А, i3 |
= 20 |
2 sin(ωt + ------ ) А; |
||
|
3 |
|
|
3 |
|
π |
|
|
|
2) i1 = 2 sinωt А, i2 = 2 sin(ωt – -- ) А; |
|
|
|
|
|
2 |
|
|
|
π |
π |
|
2π |
|
3) i1 = 10 cos(ωt + -- ) А, i2 |
= 10 cos(ωt + -- |
+ |
------ ) А, i3 = 10 cos(ωt + |
|
2 |
2 |
|
3 |
|
π4π
+-- + ------ ) А; 2 3
4)i1 = 1 sinωt А, i2 = 1 cosωt А, i3 = 1 sin(ωt + π) А, i4 = 1 cos(ωt + π) А. Изобразить токи на векторных диаграммах.
4.7.К вторичным обмоткам трехфазного трансформатора 35/10 кВ мощностью 1000 кВт подключен асинхронный двигатель АД номинальной мощностью 630 кВт. Вторичные обмотки трансформатора соединены треугольником (рис. к задаче 4.7(р)). В номинальном режиме двигатель работает с cosϕ = 0,9.
A
АД
C |
B |
Рис. к задаче 4.7
Определить фазные токи трансформатора и линейные токи двигателя: в номинальном режиме, при обрыве в цепи вторичной обмотки ВС трансформатора.
180
