
Бутырин Алексейчик Сборник задач по ТОЭ т1
.pdf
2.50. 1) С |
= 118 пФ; L = 299 мкГн; 2) Р |
= 450 Вт. |
0 |
0 |
max |
2.51.С = 296 пФ; tgδ = 0,113.
2.52.С = 55 мкФ.
2.53.Q = 0,91 Мвар; С = 24 мкФ.
2.54.U = 100 В.
р
2.55. 1,41 А. |
|
|
|
|
|
|
||
2.56. C0 |
= 100 пФ; Q = 500; UL = UC = 1 В. |
|
|
|||||
2.57. 150 B. |
|
|
|
|
|
|
||
2.58. 8 А. |
|
|
|
|
|
|
|
|
2.59. C = 100 пФ; Q = 500; Δω = 200 рад/с; ω = |
ω ω . |
|||||||
0 |
|
|
|
|
|
0 |
1 |
2 |
2.60. R = 2 Ом; XC = 1 Ом. |
|
|
|
|
|
|||
2.61. XC |
= 30 Ом; XC |
= 53,3 Ом. |
|
|
|
|||
|
1 |
|
2 |
|
|
|
|
|
2.62. Cm = 0,8 мкФ; C0 |
= 1 мкФ. |
|
|
|
||||
2.63. ω = 500 рад/с; I |
= 0; I |
= j0,1 А; I = –j0,1 А. |
|
|||||
0 |
|
1 |
|
2 |
3 |
|
|
|
2.64. XC |
= 30 Ом; XC |
= 53,3 Ом; I 1 |
= 3,057 0 А; |
|
||||
|
1 |
|
2 |
|
|
|
|
|
I |
= 1,91 –36,87° А; I |
= 1,91 36,87° А. |
|
|
||||
2 |
|
|
|
3 |
|
|
|
|
2.65. R |
= 100 Ом; C = 3,18æ10–5 Ф; P |
= 100 Вт; P = 80 Вт. |
||||||
н |
|
|
|
|
|
max |
0 |
|
2.66. L = 28,8 мГн; I |
= 1,71 А. |
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
2.67. 20 В; |
2 А; u(t) = 40 |
2 sin(1000t) В. |
|
|
||||
|
|
50 |
|
|
|
|
|
|
2.68. XC |
= |
----- Ом; Pmax = 1000 Вт. |
|
|
|
|||
|
|
7 |
|
|
|
|
|
|
2.69. 1) ХС = 10 Ом; Рmax = 100 Вт; 2) ХС = 30 Ом. |
|
|
||||||
2.70. 1) параллельный резонанс при C = 2æ10–9 Ф (Z |
= ∞ ); |
|||||||
|
|
|
|
|
|
|
вх |
|
2) последовательный резонанс при C = 40æ10–6 Ф (Z |
= R = 10 Ом). |
|||||||
|
|
|
|
|
|
|
вх |
|
2.71. Z |
= 500 + j500 Ом; Р |
= 0,903 Вт. |
|
|
||||
н |
|
|
|
н |
|
|
|
|
2.72.R = 
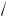 L ⁄ C .
L ⁄ C .
2.73.С = 0,1 мкФ.
2.74.1) при параллельном резонансе 3,33 мФ, 3,33мА, 20 мА, 20 мА; при последовательном резонансе 13,3 мА, 6,67 мА, 20 мА, 40 мА; 2) при параллельном резонансе 10 мА, 10 мА, 20 мА, 20 мА; при последовательном резонансе 40 мА, 20 мА, 20 мА, 40 мА.
2.75. |X | = 30 Ом; |X | = 100/3 Ом; X X < 0; P |
= 3,025 Вт; P = 1 Вт. |
||||
3 |
4 |
3 4 |
max |
|
|
2.76. |X | = 30 Ом; |X | = 100/3 Ом; X X |
< 0; P |
= 40 Вт; P |
/P = |
||
1 |
2 |
1 |
2 |
max |
max |
= 3,02 раза.
131

2.77. |X | = 100/3 Ом; |X | = 30 Ом; X X |
< 0; P = 0,331 от P . |
|||
1 |
2 |
1 |
2 |
max |
2.78. R = 100/3 Ом; XC = 25 Ом. |
|
|
|
|
2.79. UV = 250 В; UV |
= 250 В; UV |
= UV |
= 240 В. |
|
|
1 |
2 |
|
3 |
2.80.1) а и d (b и c); 2) а и c (b и d).
2.81.См. решение.
2.82.UV = 170 В.
2.83. UV = 6,37 В; UV = 7,78 В.
13
2.84.М = 6,8 мГн.
2.85. I 1 |
= 2 + j2 А; I 2 = 1 + j2 А; I |
3 = 1 А; d = 0; a = 50 В; |
b |
= –20 + j70 В; c = 20 + j40 В. |
|
2.86. I |
= 0,6 – j1,3 = 1,43 –65° А; I |
= –0,6 + j0,3 = 0,67 153,5° А; |
1 |
2 |
|
I= 1,2 – j1,6 = 2 –53° А; ϕb = 0; ϕa = 164 + j48 В; ϕc = –36 + j48 В.3
2.87. Z |
= 20 + j0 = 20 0 |
Ом. |
|
|
вх |
|
|
|
|
2.88. Z |
= j8 Ом. |
|
|
|
вх |
|
|
|
|
2.89. Z |
= j720 Ом; Z |
= j720 Ом. |
||
вх |
вх |
|
|
|
2.90. I |
= 0,91 – j4,15 |
= |
4,25 –77,7° А; I = 3,77 – j6,08 = |
|
1 |
|
|
|
2 |
= 7,15 –58,2° А; I |
|
= I |
+ I = 4,68 – j10,2 = 11,2 –65,3° А. |
|
12
2.91.UV = 97,28 В; IА = 1,08 А.
2.92.UV = 59,4 В; PW = 191,1 Вт.
2.93. UV = 100 В; UV = 0.
12
2.94. I 1 |
= 10 – j10 А; I |
2 = 5 + j5 А; I 3 = 15 – j5 А; PW = 0; |
|
|
|
|
1 |
PW = 1500 Вт; PW |
= 1500 Вт. |
||
|
2 |
3 |
|
2.95. Z |
= 129 – j300 Ом; Z = 329 + j700 Ом. |
||
внос |
|
вх |
|
2.96. U = 40 – j30 В. |
|
||
2.97. R = 0; C ≥ 4 мкФ. |
|
||
2 |
|
|
|
2.98. R2 |
= XL |
= 5 Ом. |
|
|
|
2 |
|
2.99. E |
= 50 + j100 В. |
|
|
2 |
|
|
|
2.100.UV = 25 В. |
|
||
2.101.IA |
= |
2 ⁄ 2 А; M = 0,2 Гн. |
|
|
2 |
|
|
132

Глава третья
ЛИНЕЙНЫЕ ЦЕПИ
НЕСИНУСОИДАЛЬНОГО ТОКА
ВВЕДЕНИЕ
Разложение периодических токов, напряжений, ЭДС в гармонические ряды. Ток i = i(t), удовлетворяющий условиям Дирихле, может быть представлен в виде ряда Фурье:
|
∞ |
|
|
|
|
|
∞ |
|
|
i(t)=I + |
∑ |
I |
|
sin (kωt + ψ |
|
) =I + |
∑ |
( I ′ |
sin kωt + I ″ cos kωt ) , |
0 |
|
km |
|
k |
0 |
km |
km |
||
|
k = 1 |
|
|
|
|
|
k = 1 |
|
|
(3.1) |
|
|
|
|
|
|
|
|
|
где I0 — постоянная составляющая (нулевая гармоника); I1msin(ωt + ψ1) — первая гармоника, а Ikm sin(kωt + ψk) при k > 1 — высшие гармоники
(вторая, третья и т.д.); ω = 2π/Т — основная угловая частота, т.е. угловая частота первой гармоники тока, имеющего период Т. Амплитуды и начальные фазы гармоник определяются по табл. 3.1 и соотношениям
|
|
|
2 |
2 |
|
|
Ik″m |
I |
|
= |
( I ′ ) |
+ ( I ″ ) |
, ψ |
|
= arctg---------- , k = 1, 2 … (3.2) |
|
km |
|
km |
km |
|
k |
Ik′m |
|
|
|
|
|
|
|
Аналогичным образом могут быть представлены в виде рядов периодические напряжения и ЭДС цепи.
|
|
|
|
|
|
|
|
|
Таблица 3.1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T ⁄ 2 |
|
|
|
1 |
π |
|
I |
|
-- |
∫ |
i(t) dt |
|
|
----- |
∫ |
i(ωt) d(ωt) |
0 |
|
T |
|
|
|
2π |
|
||
|
|
–T ⁄ 2 |
|
|
|
|
–π |
|
|
|
|
|
|
|
|
|
|
|
|
I′ |
2 |
T ⁄ 2 |
|
|
1 |
π |
|
|
|
-- |
∫ |
i(t) sinkωt dt |
-- |
∫ |
i(ωt) sinkωt d(ωt) |
||||
km |
T |
|
|
π |
|
|
|
||
|
|
–T ⁄ 2 |
|
|
|
–π |
|
|
|
|
|
|
|
|
|
|
|
|
|
I″ |
2 |
T ⁄ 2 |
|
|
1 |
π |
|
|
|
-- |
∫ |
i(t) coskωt dt |
-- |
∫ |
i(ωt) coskωt d(ωt) |
||||
km |
T |
|
|
π |
|
|
|
||
|
|
–T ⁄ 2 |
|
|
|
–π |
|
|
|
|
|
|
|
|
|
|
|
|
|
133
Расчет установившихся режимов в линейных цепях с использованием комплексного метода. Представив все ЭДС и токи источников в виде рядов Фурье, можно провести расчет цепи отдельно по каждой из гармоник — по нулевой гармонике (постоянному току), когда ЭДС
итоки источников тока учитываются только их постоянными составляющими; по первой гармонике, когда источники считаются синусоидальными с частотой ω и т.д. В результате определяются постоянная
игармонические составляющие токов и напряжений цепи, которые затем в соответствии с принципом суперпозиции суммируются. Так, для некоторого тока имеем
i = I0 + i1 + i2 + … + iN + … ≈ I0 + i1 + i2 + … + iN,
где I0 — постоянная, а ij, j > 1, — гармонические составляющие тока
ik = Ikm sin(kωt + ψk), k = 1, 2, …, N — номер гармоники тока, обеспечивающий требуемую точность его вычисления. Расчет первой и высших гармоник удобно проводить комплексным методом, при этом обязательно переводя его результат в вещественную (временную)′ область, так как суммировать гармоники можно только в этой области. При использовании комплексного метода необходимо пересчитывать комплексные сопротивления индуктивного Z = jXL, XL = kωL,
и емкостного Z = –jXС, XC = 1/(kωC), элементов для каждой гармо-
ники k = 1, 2, …, N. В цепях с полигармоническим воздействием, когда ЭДС и токи источников имеют вид
N N
e = ∑ Ekm sin (ωkt + ψk) и J = ∑ Ikm sin (ωkt + ψk) ,
k = 1 |
k = 1 |
где угловая частота ωk имеет не обязательно целочисленные значения,
комплексным методом рассчитываются режимы для каждой частоты ωk, а затем результаты расчетов суммируются в вещественной области.
При этом исключаются операции разложения e(t) и J(t) в ряд Фурье.
Действующие значения тока, напряжения, ЭДС. Для периодических процессов действующие значения переменных могут быть рассчитаны как
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
dt ≈ |
I |
2 |
+ |
2 |
+ |
2 |
; |
|
|
||
I = -- ∫ i |
|
0 |
I1 |
… + IN |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 T |
|
2 |
|
|
2 |
|
2 |
2 |
|
|
||||
U = -- |
∫ u dt ≈ U0 + |
U1 + … + UN; |
(3.3) |
|||||||||||
|
||||||||||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 T |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
dt ≈ |
|
|
2 |
|
2 |
+ … + |
2 |
|
|
|||
E = -- |
∫ e |
|
|
E0 |
+ E1 |
EN, |
|
|
||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
134

где I0, U0, E0 — постоянные составляющие тока, напряжения, ЭДС;
|
Ikm |
|
Ukm |
|
Ekm |
Ik |
= ------- , Uk |
= |
---------- , Ek |
= |
--------- — действующие значения k-й гармо- |
|
2 |
|
2 |
|
2 |
ники тока, напряжения, ЭДС, k = 1, 2, …, N.
Мощности в цепях с периодическими токами и напряжениями. Активную и полную мощности некоторого двухполюсника с током i = i(t) и напряжением u = u(t) можно выразить через параметры их гармоник:
∞ |
|
|
|
|
P = ∑ Pk, Pk = UkIk |
cos ϕk, P0 = U0I0; |
|
||
|
|
|||
k = 0 |
|
|
|
|
|
|
|
|
(3.4) |
|
|
|
|
|
∞ |
2 ∞ |
2 |
|
|
S = UI = ∑ Uk ∑ Ik . |
|
|
||
k = 0 |
k = 0 |
|
|
|
Отношение λ = P/S называют коэффициентом мощности.
Интегральные оценки качества несинусоидальных процессов. Периодические процессы принято характеризовать четырьмя величинами: максимальным значением тока (напряжения) Imax(Umax) за
период, его действующим значением I(U), действующим значением его первой гармоники I1(U1), а также средним по модулю значением:
1 T |
|
i(t) |
|
|
|
1 T |
|
u(t) |
|
|
|
|
|
|
|
|
|
||||||
Iср = -- ∫ |
|
|
dt , U |
ср |
= -- ∫ |
|
|
dt |
(3.5) |
||
|
|
|
|
|
|||||||
T |
|
T |
|
||||||||
0 |
|
|
|
|
|
0 |
|
|
|
|
|
и тремя коэффициентами: |
|
|
|
|
|
|
|
||||
коэффициентом формы |
|
|
|
|
|
|
|
||||
kф = I/Iср (kф = U/Uср), |
(3.6) |
||||||||||
коэффициентом амплитуды |
|
|
|
|
|
|
|
||||
kа = Imax/I (kа = Umax/U), |
(3.7) |
||||||||||
коэффициентом искажения |
|
|
|
|
|
|
|
||||
kи = I1/I (kи = U1/U). |
(3.8) |
||||||||||
Показания приборов. В зависимости от исполнения прибора (вольтметр или амперметр) и устройства его входного преобразователя он может показывать действующее значение измеряемой величины, ее среднее по модулю значение, усредненное за период положительное (отрицательное) значение и т.д. Магнитоэлектрические приборы показывают постоянную составляющую измеряемой величины; электромагнитные, электродинамические, электростатические
135

и тепловые — ее действующее значение. Показания электронных приборов в зависимости от устройства входного преобразователя могут определяться действующим, средним по модулю, максимальным или минимальным значением измеряемой величины. Прибор индукционной системы и электронный прибор с конденсатором на входе определяет действующее значение переменной составляющей измеряемой величины.
3.1. ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЦЕПЯХ
3.1(р). Разложить в тригонометрический ряд периодическую функцию напряжения, выражаемую кривыми, представленными на рис. к задаче 3.1(р).
u |
|
|
Umax |
|
|
t1 |
|
|
|
|
2 t |
2 |
|
|
–Umax |
|
|
а) |
|
|
u |
|
Umax |
|
|
2 t |
–Umax |
|
б) |
|
Рис. к задаче 3.1(р) |
|
u |
|
|
Umax |
|
|
|
2 |
t |
–Umax |
|
|
в) |
|
|
Решение. Для кривой на рис. а ωt1 = π/2, на рис. б ωt1 = 0, на рис. в
ωt1 = π.
Запишем уравнения кривой (а, в) для различных интервалов периода
|
|
Umax |
|
|
u1 |
(t) = ------------ωt, 0 ≤ ωt ≤ ωt1 |
; |
u(t) = |
|
ωt1 |
|
u2(t) = Umax, ωt1 ≤ ωt ≤ π.
По условию симметрии функция, описывающая кривую, нечетная и в разложении содержатся только синусоиды. Для определения
коэффициентов ряда U′ |
(все U″ |
= 0) воспользуемся формулой |
|||||||||||||||
|
|
|
|
|
|
km |
|
km |
|
|
|
|
|
|
|
|
|
|
2 |
ωt=ωt1 Umax |
|
|
|
|
|
ωt=π |
|
|
|
|
|||||
U′ |
= -- |
|
∫ |
------------ωt sin kωt dωt + |
∫ |
|
U |
|
sin kωt dωt . |
||||||||
km |
|
ωt |
|
|
|
|
|
|
|
|
|
max |
|
|
|||
|
π |
|
1 |
|
|
|
|
|
ωt=ωt |
|
|
|
|
||||
|
|
|
ωt=0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Коэффициенты Фурье |
|
|
|
|
|
|
|
|
|
|
|||||||
|
U′ |
|
2Umax |
|
|
1 |
|
sin kωt |
|
|
|
, |
U |
|
= U′ |
: |
|
|
|
= --------------- |
|
----------- |
|
– cos kπ |
|
||||||||||
|
km |
|
kπ |
kωt |
|
|
1 |
|
|
|
|
km |
km |
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
136
а) при ωt1 = π/2
|
U′ |
|
|
= |
|
2Umax |
2 |
sin |
kπ |
– |
cos k |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
--------------- |
|
|
|
|
|
|
|
----- |
----- |
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
km |
|
|
|
|
kπ |
|
kπ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
U |
|
|
= U ′ |
|
|
= |
1 2Umax |
|
1 |
2 |
|
|
|
|
|
, U |
|
|
|
= U ′ |
|
|
= – |
1 |
2Umax |
, |
|
|
|
||||||||||||||||||
|
|
|
|
|
-- |
--------------- |
|
|
|
|
|
-- |
-- + 1 |
|
|
|
|
|
-- |
--------------- |
|
|
|
|
|
|||||||||||||||||||||||
|
|
1m |
|
|
|
|
1m |
|
|
|
1 |
|
π |
1 π |
|
|
|
|
|
|
|
2m |
|
|
|
2m |
|
|
|
2 |
π |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
U |
|
|
= U ′ |
|
|
= |
1 2Umax |
|
– |
1 2 |
|
|
|
|
|
U |
|
|
= U ′ |
|
|
|
= – |
1 2Umax |
. |
|
|
||||||||||||||||||||
|
|
|
|
|
-- |
--------------- |
|
|
|
|
|
-- -- |
|
|
+ 1 , |
|
|
|
|
|
-- --------------- |
|
|
|
|
|
||||||||||||||||||||||
|
|
3m |
|
|
|
|
3m |
|
|
|
3 |
|
π |
|
|
|
3 π |
|
|
|
|
|
|
|
|
4m |
|
|
4m |
|
|
|
4 |
π |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Искомый ряд Фурье |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
u(t) = |
2Umax |
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
sin 2ωt |
+ |
|
1 |
– |
1 |
2 |
|
|
sin 3ωt – |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
--------------- |
|
|
|
|
|
|
|
-- -- + 1 sin ωt – |
-- |
|
|
-- |
-- |
-- |
+ 1 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
π |
|
|
|
1 π |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
+ …] ; |
|
|
3 |
|
|
3 |
π |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
4 sin 4ωt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
б) при ωt |
1 |
= 0 для k = 1 |
U′ можно получить, раскрывая неопре- |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
km |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
sin kωt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
деленность ------------------- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
kωt1 |
|
ωt |
→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4Umax |
|
|
|
2 kπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
U |
|
|
|
= |
U′ |
|
= --------------- |
|
|
|
|
|
sin |
|
-----, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
km |
|
|
|
km |
|
|
|
kπ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 4Umax |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 4Umax |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
U1m = |
1-- ---------------π |
|
, U2m = 0, U3m = |
3-- ---------------π |
|
, U4m |
= 0. |
|
|
|
|
||||||||||||||||||||||||||||||||||
Искомый ряд Фурье |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4Umax |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
u(t) = |
|
--------------- |
|
|
|
|
|
|
|
sin ωt + |
-- |
|
sin 3ωt + |
-- |
sin 5ωt + … |
; |
|
|
|
|
|||||||||||||||||||||||||
в) при ωt1 = π |
|
|
|
π |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
U |
|
|
= |
|
|
U′ |
= |
|
2Umax |
1 |
sin kπ – cos k |
|
|
|
|
2Umax |
cos kπ, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
--------------- |
|
|
|
|
----- |
π |
|
= –--------------- |
|
|
|
||||||||||||||||||||||||||||||||
|
km |
|
|
|
|
km |
|
|
|
|
|
|
kπ |
kπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kπ |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 2Umax |
|
|
|
|
|
1 2Umax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
U1m = |
1-- ---------------π |
|
|
, |
U2m |
= – |
2-- ---------------π |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 2Umax |
|
|
|
|
|
1 2Umax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
U3m = |
3-- ---------------π |
|
|
, |
U4m |
= – |
4-- ---------------π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Ряд Фурье |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2Umax |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
u(t) = |
|
|
|
|
|
|
|
|
|
sin ωt – |
-- |
|
sin 2 |
ωt + |
|
sin 3ωt – |
-- |
|
sin 4ωt + … |
. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
137
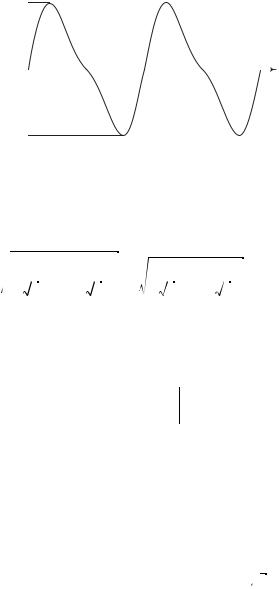
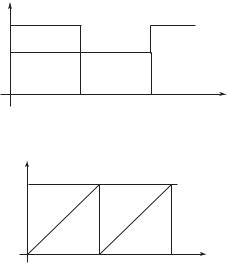
3.2(р). Вычислить коэффициенты формы, амплитуды и искажения кривой напряжения (рис. к задаче 3.2(р)), уравнение которой
u(t), В |
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
t |
||
|
|
||||
–50 |
|
|
|
|
|
|
|
|
|
|
|
–100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. к задаче 3.2(р)
u(t) = U1m sinωt + U2m sin2ωt, U1m = 100 В, U2m = 30 В.
Решение. Действующее значение напряжения
|
|
U |
|
2 |
U |
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
100 |
2 |
|
30 |
|
2 |
|
|||||
|
|
|
|
|
1m |
|
|
|
2m |
|
|
|
|
|
|
|
|||
U = |
|
|
---------- |
+ |
|
---------- |
= |
|
+ |
|
|
= 73,8 В. |
|||||||
|
|
|
|
-------- |
|
------ |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|||||
|
|
2 |
|
2 |
|
|
|
|
|||||||||||
Среднее по модулю значение |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uср |
= -- |
∫ (U1m sin ωt + U2m sin 2ωt) dωt = |
||||||||||||||||
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
1 |
|
U |
|
|
cos ωt + |
U2m |
cos 2 |
|
= |
2U1m |
= 63,7 В. |
||||||||
= –-- |
|
|
|
---------- |
ωt |
------------- |
|||||||||||||
π |
|
|
1m |
|
|
|
|
2 |
|
|
|
|
|
π |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Найдем максимальное значение напряжения u(t):
du
-------------- = U cos ωt + 2U cos 2ωt = 0. d(ωt) 1m 2m
Учитывая, что cos2ωt = 2cos2ωt – 1, получаем квадратное уравнение 120 cos2ωt + 100 cosωt – 2 = 0, следовательно,
cosωt = 0,0196, ωt = 88,9° и Umax = 101,2 В.
kф = |
73,8---------- |
= 1,16, kа = |
101,2------------- |
= 1,37, kи = |
100--------------------⁄ 2 |
= 0,96. |
|
63,7 |
|
73,8 |
|
73,8 |
|
138
3.3. Разложить в тригонометрический ряд функцию тока, график которой выражает телеграфные сигналы в случае периодической передачи точек (рис. к задаче 3.3).
i(t) |
|
|
I1max |
|
|
I2max |
|
|
|
2 |
t |
Рис. к задаче 3.3 |
|
|
u |
|
|
Umax |
|
|
|
2 |
t |
Рис. к задаче 3.4 |
|
|
3.4.Разложить в тригонометрический ряд функцию напряжения, выражаемую пилообразной кривой (рис. к задаче 3.4). По найденному выражению построить кривую, составленную из суммы постоянной составляющей и первой гармоники разложения функции, сравнить графически полученную кривую с исходной пилообразной. То же в случае добавления второй и третьей гармоники.
3.5.Разложить в тригонометрический ряд периодические функции напряжения, выражаемые кривыми прямоугольной (рис. к задаче 3.5, а)
итреугольной (рис. к задаче 3.5, б) формы.
По найденному выражению для кривой на рис. а построить сумму первой и третьей гармоник разложения, и сравнить с исходной кривой. То же в случае добавления пятой гармоники.
3.6. Напряжение имеет вид периодически ломаной кривой (рис. к задаче 3.6). Построить сумму первых трех составляющих ряда Фурье и сравнить с исходной кривой. Из общего выражения тригонометрического ряда получить частные случаи:
а) ωt1 = 2π, б) ωt1 = π, в) ωt1 = 3π/2.
139

u |
|
|
Umax |
|
|
|
2 |
t |
–Umax |
|
|
а) |
|
|
u |
|
|
|
Umax |
|
|
|
|
|
2 |
t |
2 |
|
|
|
–Umax |
|
|
|
|
б) |
|
|
u |
|
Umax |
|
2 |
t |
а) |
|
Рис. к задаче 3.5 |
||
u |
|
|
Umax |
|
|
|
2 |
t |
б) |
|
|
Рис. к задаче 3.6 |
||
u |
|
|
Umax |
|
|
3 |
2 |
t |
2 |
|
|
в) |
|
|
i(t)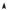
Imax
|
|
|
|
|
2 |
t |
|
Рис. к задаче 3.7
3.7.Разложить в тригонометрический ряд функцию двухполупериодного выпрямленного тока (рис. к задаче 3.7).
3.8.Разложить в тригонометрический ряд функцию, выражаемую кривой выпрямленного синусоидального тока в цепи трехфазного выпрямителя (рис. к задаче 3.8).
3.9.Определить коэффициенты формы, амплитуды и искажения для кривых, представленных на рис. к задаче 3.9, а и б.
При решении задачи действующее значение определить путем непосредственного интегрирования, а также с использованием разложения в ряд Фурье (см. Методическое замечание).
140
