2.3. Теорема о равновесии трех сил
Если к телу приложены три непараллельные взаимно уравновешивающиеся силы, то они образуют систему сходящихся сил (линии действия этих сил пересекаются в одной точке).
Д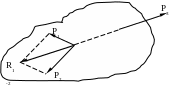
ве
силы
и
(рис.2.5) образуют равнодействующую
,
которая при равновесии сил (что считается
известным) равна силе
по модулю, лежит на одной прямой и
направлена в противоположную сторону.
Рис.2.5
Следовательно, три силы пересекаются в одной точке (и лежат в одной плоскости).
Эта теорема часто используется при поиске величины и направления одной из реакций опор конструкции, к которой приложены 3 силы.
Лекция 3 Произвольная система сил в пространстве и на плоскости
Система пар сил. Сложение пар сил Условие равновесия пар сил. Уравнения равновесия. Система сил, произвольно расположенных в пространстве. Приведение силы к центру (метод Пуансо). Сложение сил
Сложение пар сил
Е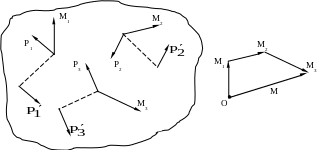
сли
к телу приложить пары сил, то можно
использовать для их сложения векторы
– моменты пар сил. Так как момент пары
сил не изменяется при переносе пары сил
в параллельную плоскость и не изменяется
при перемещении пары сил в плоскости
ее действия, то момент пары сил считается
свободным вектором (в отличие от силы
– скользящего вектора). А это означает,
что векторы – моменты пар сил можно
приложить к одной точке тела и сложить
их по правилу сложения сходящихся
векторов – построить векторный
многоугольник, замыкающая которого
определяет момент пары сил, эквивалентной
заданной системе пар сил (см. рис.3.1).
Рис.3.1
Таким образом,
,
что означает, что в результате сложения
пар сил получается одна пара сил, момент
которой равен геометрической сумме
моментов пар сил. Эту пару сил можно
представить расположенной в плоскости,
перпендикулярной к вектору
и
стремящейся повернуть тело вокруг оси,
совпадающей с вектором
против хода часовой стрелки, если
смотреть вдоль вектора
к его основанию. При этом пару сил могут
образовывать любые две силы
и
(
)
так, чтобы произведение одной из сил
пары на плечо пары сил было равно моменту
М.
Условие равновесия пар сил. Уравнения равновесия
Пары сил,
приложенные к твердому телу, взаимно
уравновешиваются, если векторный
многоугольник моментов пар сил замкнут,
т.е. если
.
Так как вектор можно определить аналитическим способом, зная моменты заданных пар сил (по аналогии с аналитическим методом определения равнодействующей сходящихся сил), т.е.
,
где 
; 
; 
,
то при равновесии пар сил
моменты пар сил должна удовлетворять
трем уравнениям равновесия 
;
; 
(алгебраическая сумма проекций моментов пар сил на каждую из прямоугольных координатных осей должна равняться нулю).
Если пары сил
лежат в одной плоскости, то следует
использовать одно уравнение равновесия
пар сил: 
.
Система сил, произвольно расположенных в пространстве
Приведение силы к центру (метод Пуансо). Сложение сил
Для сложения сил в самом общем случае широко используется метод Пуансо – приведение каждой силы к центру.
В результате
приведения силы
к центру О (рис.3.2) получаются вместо
одной три силы, из которых можно выделить
силу
,
геометрически равную заданной силе
,
приложенную к центру, и пару сил
,
момент которой
равен моменту
заданной силы
относительно центра О.
~
~
,
при этом
,
(имеется в виду, что к центру О
приложены две взаимоуравновешивающиеся
силы
и
,
параллельные и равные силе Р по
модулю, но направленные в противоположные
стороны, так что
).
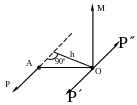
Рис.3.2
Р
ассмотрим
последовательность операций при сложении
нескольких сил, линии действия которых
не пересекаются в одной точке и не лежат
в одной плоскости (самый общий случай).
Силы
;
и
(для примера достаточно трех сил) приводим
к центру (рис.3.2) и получаем три сходящиеся
силы
;
;
и три пары сил
;
и
,
моменты которых
;
и
. Рис.3.3
Складывая
сходящиеся силы построением силового
многоугольника, получаем силу
,
приложенную к центру. Складывая моменты
пар сил построением многоугольника
моментов, получаем момент
той пары сил, которая эквивалентна трем
парам сил.
Так как момент
каждой пары сил геометрически равен
моменту заданной силы относительно
центра, следует записать
,
отсюда следует, что
,
т.е. момент пары сил, эквивалентной трем
парам сил, равен геометрической сумме
моментов заданных сил
,
и
относительно центра О. Эта сумма
моментов получила название главного
момента заданных сил относительно
центра. А сила
получила название главного вектора
заданных сил (Главный вектор нельзя
назвать равнодействующей заданной
системы сил, хотя
,
так как он один не эквивалентен заданной
системе сил; эквивалентна заданной
системе сил – совокупность силы
и пары сил, момент которой
).
Итак, в результате сложения сил, произвольно расположенных в пространстве, методом приведения их к центру получаются сила и пара сил.
Сила
,
приложенная к центру, называется главным
вектором; он равен геометрической
сумме заданных сил. Момент пары сил
равен геометрической сумме моментов
заданных сил относительно центра,
которая образует главный момент
заданных сил относительно центра
.
Нетрудно сообразить, что главный вектор не зависит от выбора центра приведения, а главный момент изменяет свою величину и направление при изменении положения центра приведения.
Возможные случаи приведения сил к центру
Сложение сил, произвольно расположенных в пространстве, методом приведения их к центру, дает различные результаты при разных значениях и .
1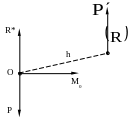
)
,
а
.
Силы приводятся к одной силе, следовательно,
заданные силы можно заменить их
равнодействующей (главный вектор
превращается в равнодействующую).
2)
,
а
.
Силы приводятся к одной паре сил, она
эквивалентна заданной системе сил. (В
этом случае вектор
не изменяет свою величину и свое
направление при изменении положения
центра приведения).
3)
и
,
но
.
Рис.3.4
В этом случае (см. рис.3.4) следует показать пару сил, соответствующую моменту , выбрав силу этой пары сил равной величине главного вектора и направив ее в сторону, противоположную главному вектору (приложив эту силу к центру приведения).
Тогда две силы
и
можно отбросить как две взаимно
уравновешивающиеся силы и останется
только одна сила
,
равная главному вектору, т.е. геометрической
сумме заданных сил. Эта сила –
равнодействующая заданных сил. Ее линия
действия отстоит от центра приведения
на расстоянии, равном плечу пары сил
,
т.е
.
4
)
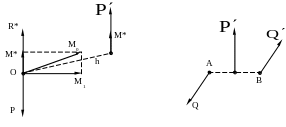и
,
но
(самый общий случай). Можно в этом случае
получить новую картину сил, если пару
сил, момент которой
,
заменить двумя парами сил, моменты
которых
и
(см. рис.3..5), причем
.
Рис.35
Покажем пару сил, соответствующую моменту , выбрав силы этой пары равными главному вектору, приложив одну из сил ( ) к центру приведения и направив ее противоположно главному вектору.
Тогда две силы и можно отбросить (см. случай 3). Остаются сила и пара сил, соответствующая моменту , расположенная в плоскости, перпендикулярной силе. Такая совокупность силы и пары сил получила название: «силовой винт» или «динама».
Определение главного вектора и главного момента системы сил относительно центра аналитическим способом
Зная силы
,
,
…
,
приложенные к твердому телу (зная их
величину и углы между силой и осями
координат), можно определить модуль и
направление главного вектора заданных
сил по способу проекций:
,
; 
; 
(аналогично определению аналитическим способом равнодействующей).
Главный момент системы сил относительно центра (его величину и направление) также можно определить по способу проекций:
,
где
- алгебраическая сумма моментов сил
относительно координатной оси Ox,
определяющая проекцию вектора
на ось Ox, которая
получила название главного момента
системы сил относительно оси -
;
(главный момент системы сил относительно
оси Oy);
(главный
момент системы сил относительно оси
Oz).
Условия равновесия сил. Уравнения равновесия
Если при сложении сил, произвольно расположенных в пространстве, силовой многоугольник получается замкнутым и векторный многоугольник моментов также получится замкнутым, то силы взаимно уравновешиваются. Следовательно, условие равновесия сил получают вид: и . Это позволяет записать условия равновесия сил в аналитической форме – уравнения равновесия:
1. ; 2. ; 3. ;
4. ; 5. ; 6. .
Получаем 6 уравнений равновесия пространственной системы сил.