
- •А.В. Индейкин б1.Б.15 «теоретическая механика»
- •23.05.06 «Строительство железных дорог, мостов и транспортных тоннелей»
- •Раздел 1 «статика»
- •Основные понятия теоретической механики
- •Статика. Аксиомы статики. Реакции связей Аксиомы статики
- •Лекция 2
- •Система сходящихся сил
- •2.1. Определение. Сложение сил геометрическим способом. Условие равновесия сил
- •3.2. Проекции силы на ось и на плоскость. Определение равнодействующей аналитическим способом. Уравнения равновесия сил
- •2.3. Теорема о равновесии трех сил
- •Лекция 3 Произвольная система сил в пространстве и на плоскости
- •Система сил, произвольно расположенных в пространстве
- •Лекция 4
- •Лекция 5 Статический расчет плоских ферм
- •Расчет усилий в стержнях фермы
- •7.1. «Способ вырезания узлов»
- •Лекция 6 Трение скольжения и трение качения
- •Сухое трение
- •Лекция 7
- •Центр параллельных сил. Центр тяжести
- •Лекция 8. Рычаг. Устойчивость против опрокидывания.
- •Лекция 9
- •Кинематика. Задачи кинематики. Кинематика точки
- •Лекция 10
- •Лекция 11
- •Лекция 12
- •Лекция 13
- •Определение ускорений точек плоской фигуры
- •Лекция 14
- •Лекция 15
- •Лекция 16
- •Абсолютное, переносное и относительное движения точки
- •Семестр 3
- •Раздел 3 динамика лекция 1
- •Лекция 2 Динамика механической системы
- •Лекция 3 Моменты инерции твердых тел
- •Лекция 4 Динамика механической системы
- •Лекция 5 Количество движения механической точки и механической системы
- •Лекция 6 Динамика вращательного и плоского движения твердого тела
- •Лекция 7
- •Лекция 8
- •Лекция 9
- •Лекция 10
- •Лекция 11 Принцип возможных перемещений
- •Лекция 12 общее уравнение динамики
- •Лекция 13
- •Лекция 14
- •Уравнения Лагранжа II рода
- •Лекция 15
- •Лекция 16 Свободные и вынужденные колебания механической системы с одной степенью свободы.
Лекция 16 Свободные и вынужденные колебания механической системы с одной степенью свободы.
Виды колебаний. Свободные колебания линейной механической системы с одной степенью свободы без учета сопротивления. Влияние вязкого сопротивления на свободные колебания линейной механической системы с одной степенью свободы.
Виды колебаний.
По признаку физического единства колебательных движений различают свободные и вынужденные колебания.
Свободными называются механические колебания автономных систем, обусловленные начальным запасом механической энергии и происходящие без воздействия вынуждающей силы.
Вынужденные колебания – это механические колебания, вызванные и поддерживаемые вынуждающей силой или кинематическим возбуждением.
Кроме свободных и вынужденных колебаний существуют иные типы колебаний, принципиально отличающиеся от них. Это, во первых, параметрические колебания – механические колебания, вызванные и поддерживаемые параметрическим возбуждением, когда колебания происходят в связи с изменением во времени одного или нескольких параметров системы (массы, момента инерции, коэффициента жесткости и др.)..
Другим самостоятельным типом колебаний являются автоколебания – асимптотически устойчивые периодические колебания автоколебательной системы, как правило, поддерживаемые за счет энергии, поступающей от неколебательных источников энергии.
Обратимся вначале к изучению свободных колебаний.
Свободные колебания линейной механической системы с одной степенью свободы без учета сопротивления
Рассмотрим механическую систему с одной степенью свободы, находящуюся только под действием сил, имеющих потенциал. Пусть кинетическая и потенциальная энергии системы приведены к виду:
; , (17.1)
где а и с − коэффициенты инерции и жесткости; , − обобщенная координата и обобщенная скорость системы.
Подставляя (17.1) в уравнения Лагранжа II рода (15.20), получаем
![]() .
.
Или
![]() ,
(17.2)
,
(17.2)
где
![]() − циклическая (собственная) частота
свободных колебаний.
− циклическая (собственная) частота
свободных колебаний.
Уравнение (17.2) представляет собой дифференциальное уравнение свободных колебаний механической системы с одной степенью свободы без учета сопротивления.
Решение дифференциального уравнения (20.2) ищем в виде:
![]() , (17.3)
, (17.3)
где А − амплитуда свободных колебаний; − начальная фаза колебаний.
Продифференцируем это равенство по времени:
![]() (17.4)
(17.4)
Постоянные интегрирования А и ,
определим из начальных условий. Пусть
в момент времени t=0
начальная обобщенная координата имела
значение q(t=0)=q0,
а начальная обобщенная скорость −
значение
![]() .
Подставляя эти условия в (17.3) и (17.4),
находим:
.
Подставляя эти условия в (17.3) и (17.4),
находим:
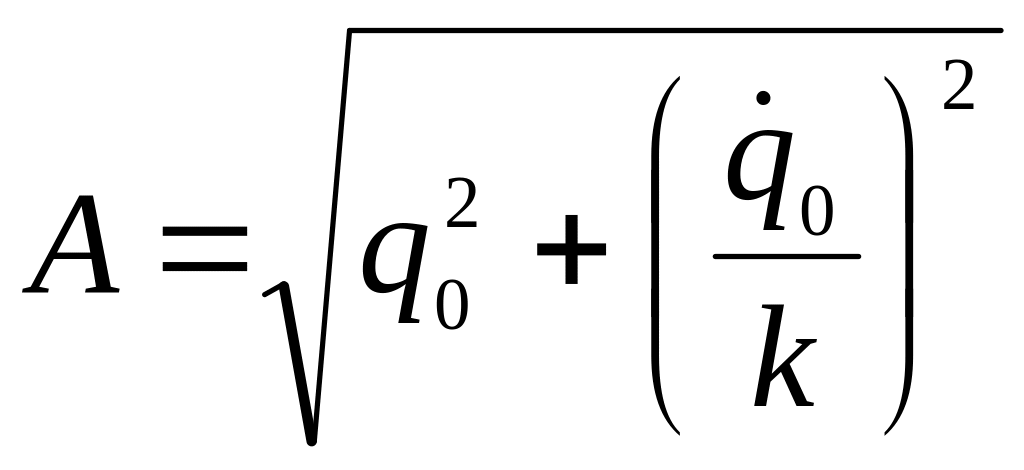 ;
;
![]() .
.
Период свободных колебаний определяется формулой:
![]() .
.
График свободных колебаний показан на рис. 17.1.
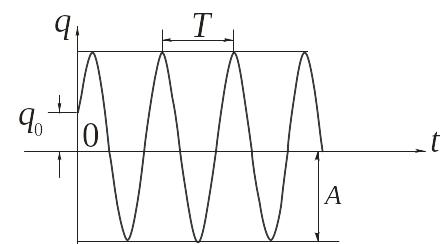
Рис. 17.1
Движение механической системы часто удобно представить на фазовой плоскости.
Состояние системы в каждый момент времени t характеризуется значениями обобщенной координаты q и обобщенной скорости . На декартовой плоскости будем откладывать по оси абсцисс обобщенную координату x=q, а по оси ординат − обобщенную скорость y= .
Точка с координатами
![]() называется изображающей точкой, а
указанная плоскость − фазовой
плоскостью.
называется изображающей точкой, а
указанная плоскость − фазовой
плоскостью.
При движении системы изменяются ее фазовые координаты q и , поэтому изображающая точка будет перемещаться по фазовой плоскости, двигаясь по некоторой линии, называемой фазовой траекторией.
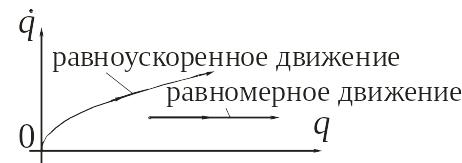
Рис. 17.2
На рис.17.2 показаны фазовые траектории материальной точки, совершающей равномерное и равноускоренное движения.
Совокупность всех фазовых траекторий называют фазовой диаграммой или фазовым портретом механической системы.
Построение фазовых траекторий особенно удобно для колебательных процессов. Например, для свободных колебаний механической системы с одной степенью свободы, исключив время t из уравнений (17.3) и (17.4), получим уравнение эллипса:

![]() .
.
Фазовый портрет этой системы показан на рис. 17.3

Рис. 17.3
Точка О называется особой точкой типа центр.
Полная механическая энергия Н0 рассматриваемой консервативной системы в процессе колебаний сохраняется:
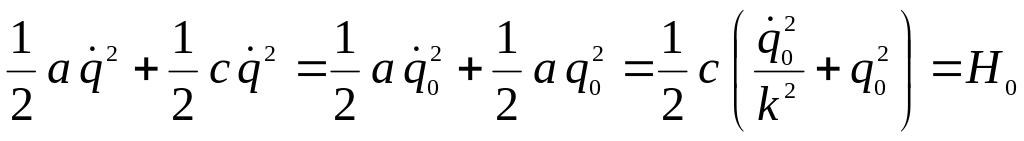 .
(17.5)
.
(17.5)
Обратим внимание на то, что площадь, охватываемая фазовой траектории в виде эллипса, равна
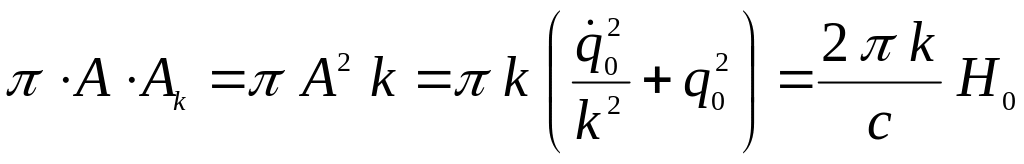 , (17.6)
, (17.6)
Сравнение (20.5) и (20.6) показывает, что
площадь, охватываемая фазовой траекторией,
пропорциональна полной механической
энергии
![]() системы.
системы.
Влияние вязкого сопротивления на свободные колебания линейной механической системы с одной степенью свободы
Рассмотрим механическую систему с одной степенью свободы, находящуюся под действием сил, имеющих потенциал и сил вязкого сопротивления. Предположим, что кинетическая и потенциальные энергии этой системы выражаются формулами:
![]() ;
; ![]() , (17.7)
, (17.7)
где
![]() и
и
![]() коэффициенты инерции и жесткости
системы.
коэффициенты инерции и жесткости
системы.
Запишем уравнения Лагранжа II рода в виде:
![]() , (17.8)
, (17.8)
где
![]() обобщенная сила вязкого сопротивления.
обобщенная сила вязкого сопротивления.
Если силы сопротивления, действующие на точки механической системы, пропорциональны первой степени скорости, то такое сопротивление называется вязким:
![]() ,
,
где
![]() - коэффициент вязкого сопротивления.
- коэффициент вязкого сопротивления.
Найдем обобщенную силу вязкого
сопротивления
![]() .
.
В соответствии с (15.4) имеем
![]() . (17.9)
. (17.9)
Так как
![]() ,
то с учетом (17.8), получаем:
,
то с учетом (17.8), получаем:
![]() ;
;
![]() , (17.10)
, (17.10)
где
![]() диссипативная функция Релея
(функция рассеяния).
диссипативная функция Релея
(функция рассеяния).
Преобразуем функцию рассеяния Ф:
![]() .
.
Отсюда
![]() ,
,
где обозначено
![]() .
.
Разложим нелинейный коэффициент
![]() в ряд Маклорена по степеням обобщенной
скорости
:
в ряд Маклорена по степеням обобщенной
скорости
:
![]()
и сохраним только первое слагаемое
![]() в этом разложении
в этом разложении
![]() .
.
Тогда функция Релея принимает вид:
![]() . (17.11)
. (17.11)
Подставляя (17.7) и (17.11) в (17.8), получаем
![]() .
.
Отсюда
![]() , (17.12)
, (17.12)
где
![]() - коэффициент затухания;
- коэффициент затухания;
![]() .
.
Уравнение (17.12) при n<k называется дифференциальным уравнением свободных колебаний при наличии вязкого сопротивления.
Для интегрирования дифференциального уравнения (17.12) составим характеристическое уравнение:
![]() . (17.13)
. (17.13)
Корни этого уравнения
![]() . (17.14)
. (17.14)
Рассмотрим три случая.
а)
![]() (случай затухающих колебаний).
(случай затухающих колебаний).
В этом случае характеристическое уравнение (17.13) имеет два комплексно-сопряженных корня
![]() .
.
Тогда общее решение уравнения (21.6) можно записать следующим образом
![]() ,
(17.15)
,
(17.15)
где
и
![]() постоянные интегрирования;
постоянные интегрирования;
![]() частота затухающих колебаний.
частота затухающих колебаний.
Постоянные
и
определяются с использованием начальных
условий. Пусть известно, что в начальный
момент времени
![]() ,
,
![]() .
.
Найдем выражение для обобщенной скорости системы. Для этого продифференцируем по времени обе части равенства (17.15):
![]() . (17.16)
. (17.16)
Подставим в (17.15) и (17.16) начальные условия:
![]() ;
;
![]() .
.
Из этих уравнений находим:
 ;
; 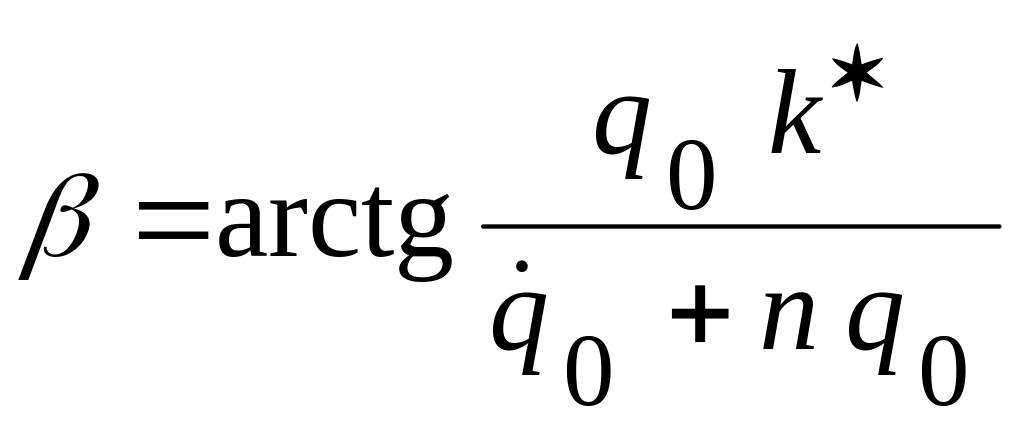 .
.
Движение, определяемое уравнением (17.15), носит колебательный характер. График затухающих колебаний показан на рис. 21.1.
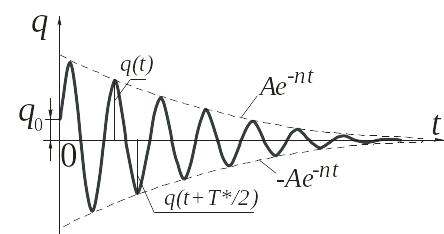
Рис. 17.4
Период затухающих колебаний
![]() больше периода колебаний
больше периода колебаний
![]() системы
без учета вязкого сопротивления. Однако,
при малом сопротивлении
системы
без учета вязкого сопротивления. Однако,
при малом сопротивлении
![]() .
.
Амплитуда затухающих колебаний уменьшается с течением времени по экспоненциальному закону.
Найдем отношение двух последовательных
максимальных значений обобщенной
координаты в моменты времени
![]() и
(рис.17.4):
и
(рис.17.4):
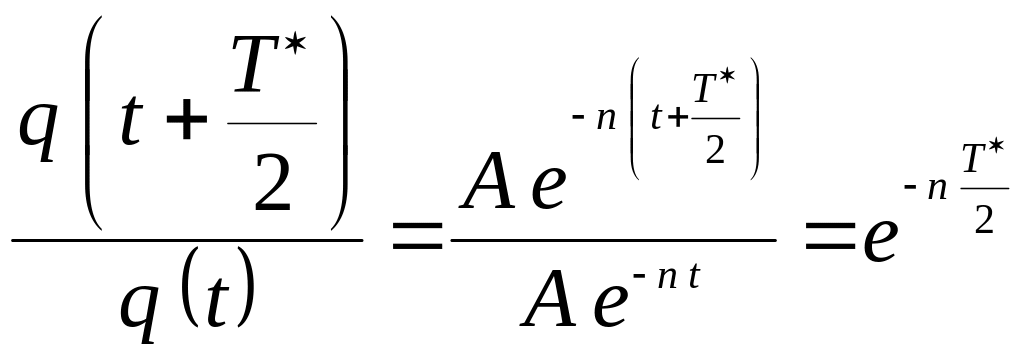 .
.
Отвлеченное число
![]() называется декрементом колебаний,
а натуральный логарифм декремента, т.е.
число
называется декрементом колебаний,
а натуральный логарифм декремента, т.е.
число
![]() логарифмическим декрементом
колебаний.
логарифмическим декрементом
колебаний.
Отметим, что даже при малых значениях коэффициента затухания амплитуда колебаний быстро уменьшается.
На рис.17.5 показан фазовый портрет механической системы, совершающей затухающие колебания.
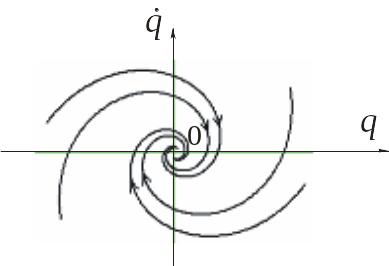
Рис. 17.5
Точка
![]() представляет собой особую точку фазовых
траекторий, которая называется устойчивым
фокусом.
представляет собой особую точку фазовых
траекторий, которая называется устойчивым
фокусом.
б)
![]() (случай апериодического движения).
(случай апериодического движения).
В этом случае характеристическое уравнение (17.13) имеет два различных действительных корня
![]() .
.
Общее решение дифференциального уравнения (17.12) можно представить в форме
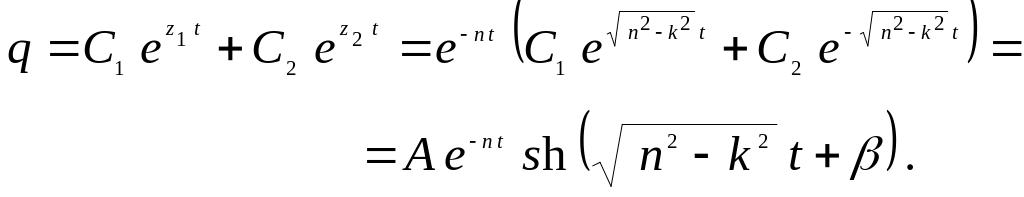 (17.17)
(17.17)
Постоянные интегрирования
![]() и
и
![]() (либо А и )
обычным образом определяются из начальных
условий
,
.
(либо А и )
обычным образом определяются из начальных
условий
,
.
Выражение (17.17) представляет собой уравнение апериодического движения, графики которого при разных начальных условиях показаны на рис. 17.6 а, б и в.

Рис. 17.6
в) n=k. В этом случае характеристическое уравнение (17.13) имеет два одинаковых (кратных) корня z1,2=-n, а следовательно, общее решение дифференциального уравнения (17.12) имеет вид:
![]() . (17.18)
. (17.18)
Для определения постоянных интегрирования и продифференцируем это выражение по времени:
![]() .
(17.19)
.
(17.19)
Предположим, что в начальный момент времени при t=0 обобщенная координата , а обобщенная скорость . Подставляя эти начальные условия в (17.18) и (17.19), находим:
q0=C2,
![]() ,
,
откуда
![]() .
.
Определив постоянные интегрирования, запишем решение (17.18) в виде:
![]() .
(17.20)
.
(17.20)
Уравнение (17.20) также как уравнение (17.17) определяет апериодическое движение.
Вынужденные колебания линейной механической системы с одной степенью свободы без учета сопротивления. Явление резонанса. Явление биений. Влияние вязкого сопротивления на вынужденные колебания линейной механической системы с одной степенью свободы.
Вынужденные колебания линейной механической системы с одной степенью свободы без учета сопротивления
Рассмотрим случай, когда на линейную
механическую систему с одной степенью
свободы действует гармоническая
возмущающая сила, которой соответствует
обобщенная сила:
![]() ,
где Р0 и p −
амплитуда и частота изменения возмущающей
силы. Сопротивление движению системы
не учитывается.
,
где Р0 и p −
амплитуда и частота изменения возмущающей
силы. Сопротивление движению системы
не учитывается.
Пусть кинетическая и потенциальная энергии системы приведены к виду: ; , где а и с − коэффициенты инерции и жесткости; , − обобщенная координата и обобщенная скорость системы.
Подставляя кинетическую Т и потенциальную энергии, а также обобщенную силу QP в уравнения Лагранжа II рода
![]() ,
,
получаем
![]() .
.
Или
![]() , (18.1)
, (18.1)
где
− собственная частота колебаний;
![]() .
.
Уравнение (18.1) представляет собой дифференциальное уравнение вынужденных колебаний механической системы с одной степенью свободы без учета сопротивления.
Решение дифференциального уравнения (18.1) ищем в виде:
![]() , (18.2)
, (18.2)
где
![]() и
и
![]() − некоторые подлежащие определению
произвольные постоянные.
− некоторые подлежащие определению
произвольные постоянные.
Продифференцируем это выражение по времени:
![]() .
.
На выбор постоянных и наложим дополнительное условие:
![]() . (18.3)
. (18.3)
Тогда
![]() .
.
Найдем вторую производную по времени:
![]() .
(18.4)
.
(18.4)
Подставляя (18.2) и (18.4) в (18.1), получаем:
![]() . (18.5)
. (18.5)
Решаем уравнения (18.3) и (18.5) как систему и находим:
![]() ,
,
![]() .
.
Интегрируя по времени, получаем:
![]() ,
,
![]() ,
,
где В1 и В2 − постоянные интегрирования.
Подставляя эти выражения в (18.2), приходим к соотношению:
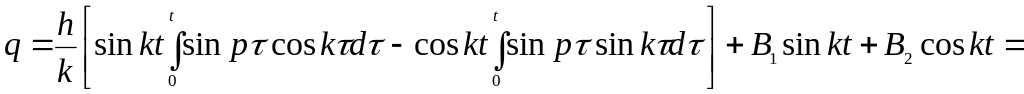
![]() .
(18.6)
.
(18.6)
Отсюда
![]() .
(18.7)
.
(18.7)
Постоянные интегрирования В1
и В2 определим из (18.6) и (18.7) с
учетом начальных условий (при t=0
![]() ,
,
![]() ):
):
![]() ,
,
![]() . (18.8)
. (18.8)
Вычислим интеграл, входящий в (18.7):
![]() .
(18.9)
.
(18.9)
Подставляя (18.8) и (18.9) в (18.6), после простых преобразований получим уравнение колебательного движения механической системы:
![]() .
(18.10)
.
(18.10)
Первые два слагаемых, входящих в это
выражение, изменяются по гармоническому
закону с собственной частотой k
системы, зависят от начальных условий
![]() ,
,
![]() и поэтому соответствуют свободным
колебаниям. Последнее слагаемое тоже
описывает гармонические колебания, но
с частотой p изменения
возмущающей силы. Это слагаемое
соответствуют вынужденным колебаниям
и поэтому соответствуют свободным
колебаниям. Последнее слагаемое тоже
описывает гармонические колебания, но
с частотой p изменения
возмущающей силы. Это слагаемое
соответствуют вынужденным колебаниям
![]() :
:
![]() . (18.11)
. (18.11)
Выражение (18.11) показывает, что при действии гармонической возмущающей силы на линейную механическую систему, она совершает сложное колебательное движение, представляющее собой результат наложения свободных и вынужденных колебаний.
Явление резонанса
Исследуем зависимость амплитуды
вынужденных колебаний
![]() от частоты p возмущающей
силы. Для этого введем так называемый
коэффициент динамичности
от частоты p возмущающей
силы. Для этого введем так называемый
коэффициент динамичности
![]() , где
, где ![]() .
.
![]() .
.
График зависимости
![]() показан на рис. 18.1.
показан на рис. 18.1.
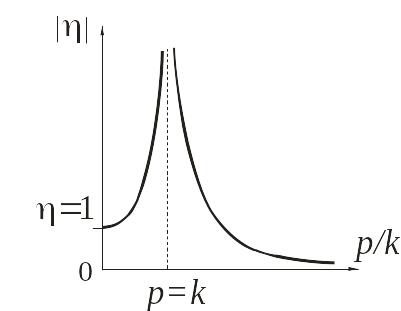
Рис. 18.1
График показывает, что с увеличением
частоты p от 0 до p=k
модуль коэффициента динамичности
![]() растет от 1 до бесконечности, а затем
уменьшается от бесконечности до нуля.
При p=k
модуль коэффициента динамичности равен
бесконечности (явление резонанса).
растет от 1 до бесконечности, а затем
уменьшается от бесконечности до нуля.
При p=k
модуль коэффициента динамичности равен
бесконечности (явление резонанса).
Явление резонанса наступает при совпадении частот свободных и вынужденных колебаний механической системы (при p=k). При этом амплитуда вынужденных колебаний обращается в бесконечность.
Дифференциальное уравнение вынужденных
колебаний механической системы при
резонансе приобретает вид: ![]() .
.
Для получения общего решения этого
дифференциального уравнения устремим
частоту p к k
и найдем предел, к которому стремится
выражение (18.10) при
![]() :
:
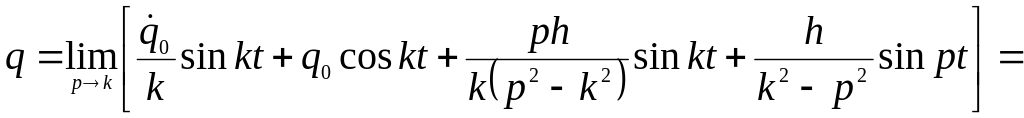
![]()
При вычислении предела, входящего в это
выражение, возникает неопределенность
типа
![]() ,
которую можно раскрыть по правилу
Лопиталя:
,
которую можно раскрыть по правилу
Лопиталя:
![]() .
.
Тогда окончательно получаем:
![]() . (18.12)
. (18.12)
Уравнение движения колебательной
системы при резонансе (18.12) показывает,
что это движение является результатом
наложения свободных и вынужденных
колебаний. Частота и период вынужденных
колебаний при резонансе равны частоте
и периоду свободных колебаний системы,
а их амплитуда изменяется пропорционально
времени. На рис. 18.2 показан график
вынужденных колебаний механической
системы при резонансе для случая нулевых
начальных условий (![]() ,
,![]() ).
).

Рис. 18.2
Явление биений
Рассмотрим случай, когда частота
вынужденных колебаний p
близка к собственной частоте k
колебаний механической системы, но не
равна ей (pk).
Тогда
![]() ,
и, следовательно,
,
и, следовательно,
![]() .
.
Воспользуемся готовым результатом вычисления интеграла (18.9):
![]()
![]() .
.
Подставляя в (18.7), получим:
![]() . (18.13)
. (18.13)
Как обычно, найдем обобщенную скорость:
![]() .
.
(18.14)
Пусть начальные условия задачи имеют вид: при t=0 , .
Тогда из уравнений (18.13) и (18.14) находим: ![]() ,
,
![]() .
.
Отсюда
![]() .
.
Окончательно получаем:
![]() .
(18.15)
.
(18.15)
Это равенство можно переписать в виде:
![]() , (18.16)
, (18.16)
где
 − амплитуда вынужденных колебаний;
− амплитуда вынужденных колебаний;
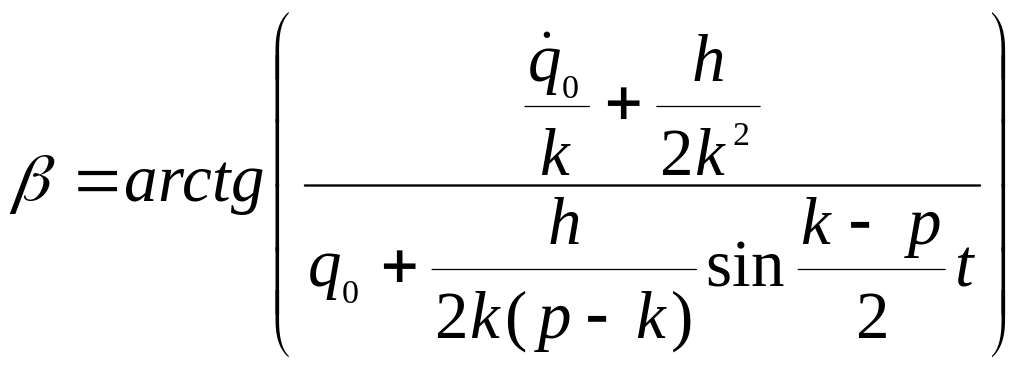 − начальная фаза
− начальная фаза
Уравнение (18.16) описывает движение, называемое биениями. В этом движении амплитуда вынужденных колебаний Aв(t) является периодической функцией времени. График колебаний, описываемых уравнением (18.16), показан на рис. 18.3.
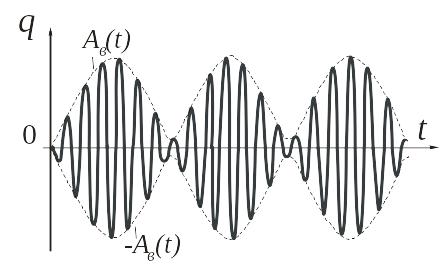
Рис. 18.3
Влияние вязкого сопротивления на вынужденные колебания линейной механической системы с одной степенью свободы
Перейдем теперь к изучению движения
линейной механической системы, на
которую помимо гармонической возмущающей
силы
![]() ,
где Р0 и p −
амплитуда и частота изменения возмущающей
силы, действуют силы вязкого сопротивления.
,
где Р0 и p −
амплитуда и частота изменения возмущающей
силы, действуют силы вязкого сопротивления.
Предположим, что кинетическая и потенциальная энергии системы приведены к виду: ; , где а и с − коэффициенты инерции и жесткости; , − обобщенная координата и обобщенная скорость системы, а диссипативная функция Релея записывается следующим образом:
,
где b − коэффициент, характеризующий силы вязкого сопротивления.
Обобщенную силу вязкого сопротивления найдем по формуле (17.4):
.
Подставляя Т, П, QP и QR в уравнения Лагранжа II рода
![]() ,
,
получаем:
![]() .
.
Отсюда
![]() ,
(18.17)
,
(18.17)
где
![]() коэффициент затухания;
.
коэффициент затухания;
.
Уравнение (22.17) представляет собой дифференциальное уравнение вынужденных колебаний линейной механической системы при наличии вязкого сопротивления.
Обще решение линейного дифференциального уравнения (18.17) будем искать в виде суммы общего решения q1 однородного уравнения (17.6) и частного решения q2 неоднородного уравнения (17.7):
q=q1+q2. (18.18)
Общее решение q1 получено выше и в зависимости от соотношения между параметрами k и n имеет вид (17.9), (17.11) и (17.12).
Частное решение q2 найдем способом неопределенных коэффициентов. Для этого будем искать q2 в виде:
![]() ,
(18.19)
,
(18.19)
где Ав, — некоторые пока неизвестные постоянные.
Найдем первую и вторую производные по времени:
![]() ,
,
![]() . (18.20)
. (18.20)
Преобразуем правую часть уравнения (18.17):
![]() .
.
(18.21)
Подставим (18.19), (18.20) и (18.21) в (18.17):
![]()
Для того, чтобы это равенство выполнялось
в любой момент времени, необходимо
приравнять коэффициенты при
![]() и
и
![]() в обеих частях этого уравнения:
в обеих частях этого уравнения:
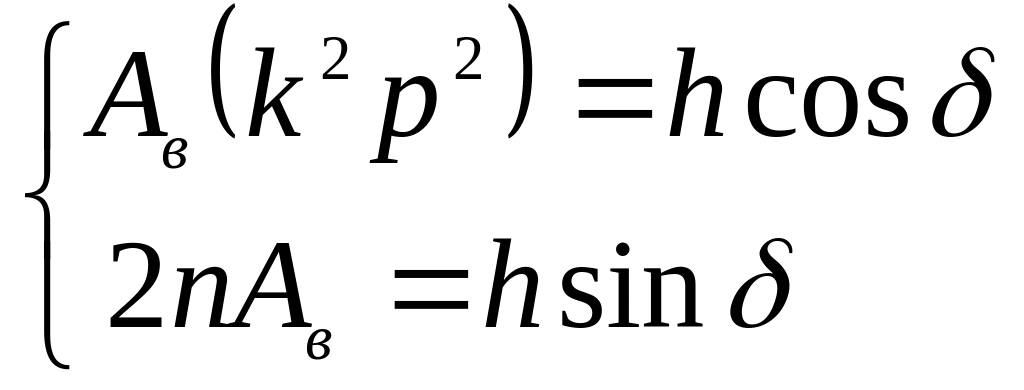 .
.
Решая эту систему, определяем постоянные Ав, :
![]() ,
,
![]() .
.
Перепишем выражение (18.17) в виде:
![]() .
(18.22)
.
(18.22)
Таким образом, общее решение дифференциального уравнения (18.17) в зависимости от соотношения между k и n выглядит следующим образом:
при
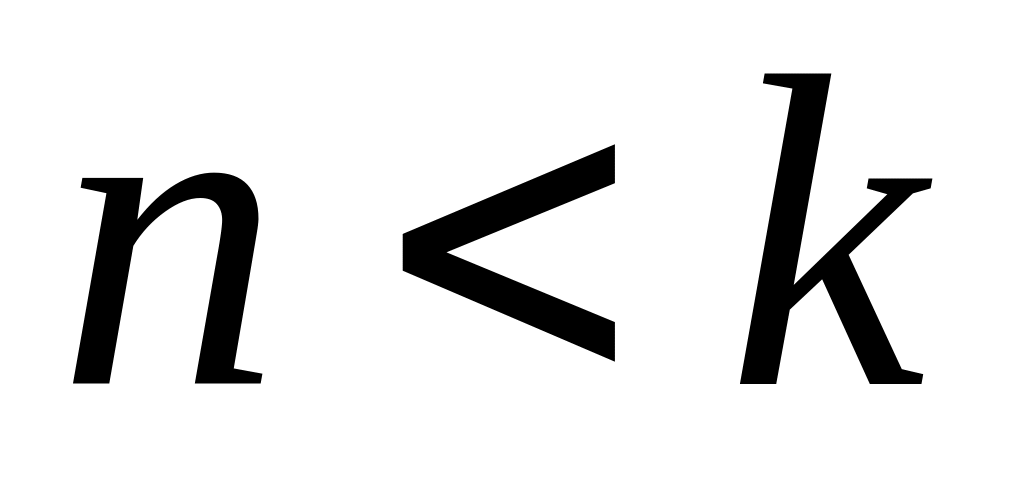
![]() ; (18.23)
; (18.23)
при
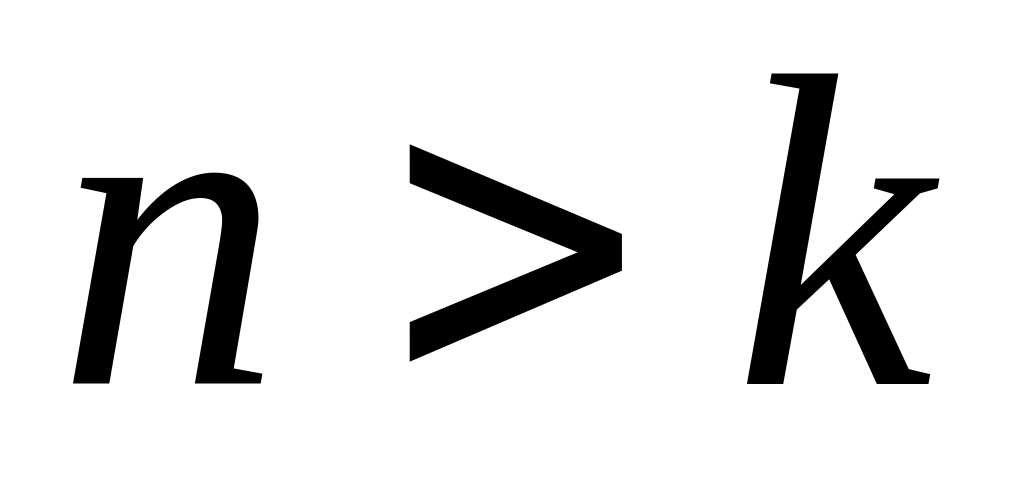
![]() ;
(18.24)
;
(18.24)
при

![]() . (18.25)
. (18.25)
Постоянные А, ,
С1 и С2 в этих уравнениях
представляют собой постоянные
интегрирования, определяемые по начальным
условиям (при t=0
,
![]() ).
).
Уравнения (18.22)-(18.24) показывают, что
движение линейной механической системы,
описываемое этими уравнениями,
представляет собой наложение затухающих
колебаний (при
)
или апериодического движения (при
![]() )
на собственно вынужденные колебания.
При этом первые слагаемые в (18.22)-(18.24),
содержащие экспоненциальный множитель
)
на собственно вынужденные колебания.
При этом первые слагаемые в (18.22)-(18.24),
содержащие экспоненциальный множитель
![]() ,
быстро уменьшаются с течением времени.
Поэтому в установившемся режиме движение
практически представляет собой только
собственно вынужденные колебания,
происходящие по закону (18.22):
,
быстро уменьшаются с течением времени.
Поэтому в установившемся режиме движение
практически представляет собой только
собственно вынужденные колебания,
происходящие по закону (18.22):
.
Исследуем вынужденные колебания линейной механической системы при наличии сил вязкого сопротивления.
Уравнение (18.22) показывает, что движение системы представляет собой гармонические колебания. Их амплитуда не изменяется с течением времени. Это объясняется тем, что потери энергии на преодоление сопротивления движению системы в точности компенсируются притоком энергии от источника колебаний.
Частота вынужденных колебаний системы
при наличии вязкого сопротивления равна
частоте p изменения
возмущающей силы, а фаза этих колебаний
![]() )
отстает от фазы возмущающей силы (pt)
на величину ,
называемую сдвигом фазы. Сдвиг фазы
изменяется в пределах
)
отстает от фазы возмущающей силы (pt)
на величину ,
называемую сдвигом фазы. Сдвиг фазы
изменяется в пределах
![]() и определяется формулой
и определяется формулой
![]() .
.
Графики зависимости сдвига фазы
от отношения частот
![]() для различных значений коэффициента
затухания n показаны
на рис. 18.4.
для различных значений коэффициента
затухания n показаны
на рис. 18.4.
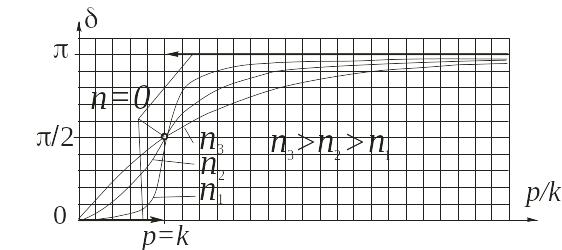
Рис. 18.4
Для выявления зависимости амплитуды
вынужденных колебаний системы от частоты
p изменения возмущающей
силы определим коэффициент динамичности
как отношение
амплитуды вынужденных колебаний
![]() к статическому отклонению системы под
действием силы Р0:
к статическому отклонению системы под
действием силы Р0:
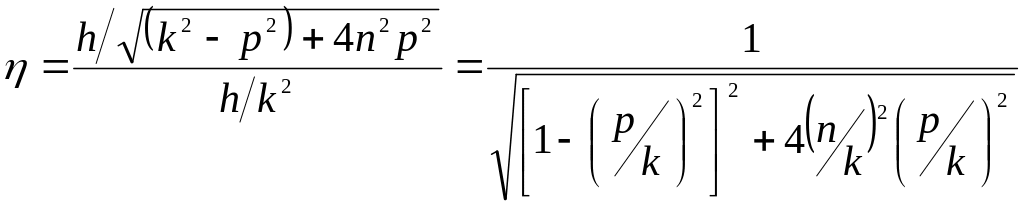 .
.
Графики зависимостей
![]() при различных значениях коэффициента
затухания n показаны
на рис. 18.5.
при различных значениях коэффициента
затухания n показаны
на рис. 18.5.
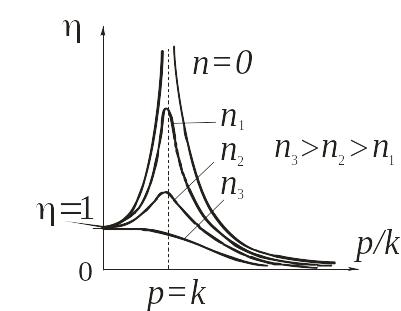
Рис. 18.5
1
Центр масс является частным случаем
общего понятия – центра H
приложенных векторов (центра Гамильтона),
радиус-вектор
![]() которого определяется формулой:
которого определяется формулой:
![]() ,
,
где
![]() – радиус-вектор центра приведения О;
– радиус-вектор центра приведения О;
![]() ,
,
![]() ,
,
![]() – главный вектор, главный момент и
главный вириал системы векторов
относительно центра приведения О.
– главный вектор, главный момент и
главный вириал системы векторов
относительно центра приведения О.
